【数学】2018届一轮复习苏教版（理）第一章集合与常用逻辑用语1-1集合与元素学案

【数学】2018届一轮复习苏教版（理）第一章集合与常用逻辑用语1-1集合与元素学案

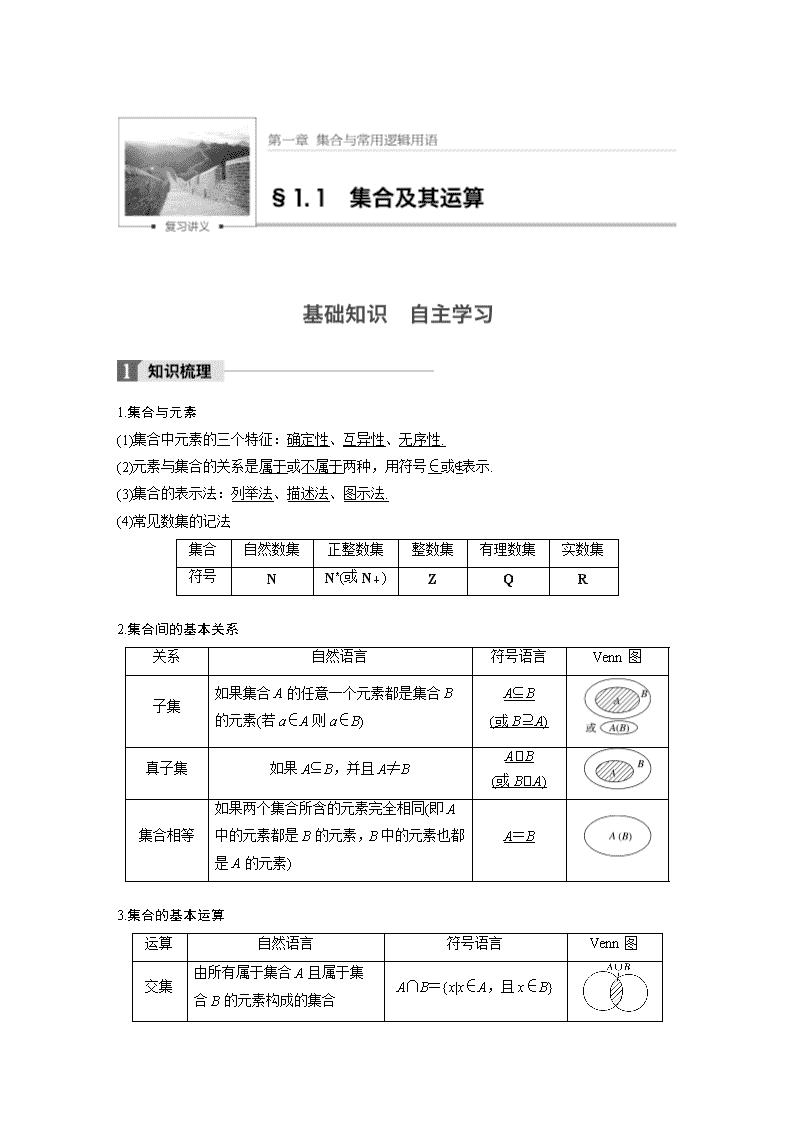
‎1.集合与元素 ‎(1)集合中元素的三个特征：确定性、互异性、无序性.‎ ‎(2)元素与集合的关系是属于或不属于两种，用符号∈或∉表示.‎ ‎(3)集合的表示法：列举法、描述法、图示法.‎ ‎(4)常见数集的记法 集合 自然数集 正整数集 整数集 有理数集 实数集 符号 N N*(或N＋)‎ Z Q R ‎2.集合间的基本关系 关系 自然语言 符号语言 Venn图 子集 如果集合A的任意一个元素都是集合B的元素(若a∈A则a∈B)‎ A⊆B ‎(或B⊇A)‎ 真子集 如果A⊆B，并且A≠B AB ‎(或BA)‎ 集合相等 如果两个集合所含的元素完全相同(即A中的元素都是B的元素，B中的元素也都是A的元素)‎ A＝B ‎3.集合的基本运算 运算 自然语言 符号语言 Venn图 交集 由所有属于集合A且属于集合B的元素构成的集合 A∩B＝{x|x∈A，且x∈B}‎ 并集 由所有属于集合A或者属于集合B的元素构成的集合 A∪B＝{x|x∈A，或x∈B}‎ 补集 设A⊆S，由S中不属于A的所有元素组成的集合称为S的子集A的补集 ‎∁SA＝{x|x∈S，且x∉A}‎ ‎【知识拓展】‎ ‎1.若有限集A中有n个元素，则集合A的子集个数为2n，真子集的个数为2n－1.‎ ‎2.A⊆B⇔A∩B＝A⇔A∪B＝B.‎ ‎3.A∩∁UA＝∅；A∪∁UA＝U；∁U(∁UA)＝A.‎ ‎【思考辨析】‎ 判断下列结论是否正确(请在括号中打“√”或“×”)‎ ‎(1)任何一个集合都至少有两个子集.(　×　)‎ ‎(2){x|y＝x2＋1}＝{y|y＝x2＋1}＝{(x，y)|y＝x2＋1}.(　×　)‎ ‎(3)若{x2，1}＝{0，1}，则x＝0，1.(　×　)‎ ‎(4){x|x≤1}＝{t|t≤1}.(　√　)‎ ‎(5)对于任意两个集合A，B，关系(A∩B)⊆(A∪B)恒成立.(　√　)‎ ‎(6)若A∩B＝A∩C，则B＝C.(　×　)‎ ‎1.(教材改编)设A＝{x|x2－4x－5＝0}，B＝{x|x2＝1}，则A∪B＝__________.‎ 答案　{－1，1，5}‎ 解析　∵A＝{－1，5}，B＝{－1，1}，‎ ‎∴A∪B＝{－1，1，5}.‎ ‎2.已知集合A＝{x|x2－6x＋5≤0}，B＝{x|y＝}，则A∩B＝__________.‎ 答案　{x|3≤x≤5}‎ ‎3.(教材改编)设全集U＝R，A＝{x|x<1}，B＝{x|x≥m}.若A∩B＝∅，A∪B＝R，则m＝________.‎ 答案　1‎ 解析　∵A∩B＝∅，A∪B＝R，∴B＝∁UA，故m＝1.‎ ‎4.(2016·天津改编)已知集合A＝{1，2，3，4}，B＝{y|y＝3x－2，x∈A}，则A∩B＝________.‎ 答案　{1，4}‎ 解析　因为集合B中，x∈A，所以当x＝1时，y＝3－2＝1；‎ 当x＝2时，y＝3×2－2＝4；‎ 当x＝3时，y＝3×3－2＝7；‎ 当x＝4时，y＝3×4－2＝10；‎ 即B＝{1，4，7，10}.‎ 又因为A＝{1，2，3，4}，所以A∩B＝{1，4}.‎ ‎5.集合A＝{x|x－2<0}，B＝{x|x－1.‎ ‎(2)由题意可得{a，a2}＝{4，16}，∴a＝4.‎ 思维升华　(1)一般来讲，集合中的元素若是离散的，则用Venn图表示；集合中的元素若是连续的实数，则用数轴表示，此时要注意端点的情况.‎ ‎(2)运算过程中要注意集合间的特殊关系的使用，灵活使用这些关系，会使运算简化.‎ ‎　(1)已知A＝{x|2a≤x≤a＋3}，B＝{x|x>5}，若A∩B＝∅，则实数a的取值范围为__________.‎ ‎(2)已知集合A＝{x|x2－x－12≤0}，B＝{x|2m－13　(2)[－1，＋∞)‎ 解析　(1)要使A∩B＝∅，则或2a>a＋3，‎ ‎∴a≤2或a>3.‎ ‎(2)由x2－x－12≤0，得(x＋3)(x－4)≤0，即－3≤x≤4，所以A＝{x|－3≤x≤4}.又A∩B＝B，所以B⊆A.‎ ‎①当B＝∅时，有m＋1≤2m－1，解得m≥2.‎ ‎②当B≠∅时，有解得－1≤m<2.‎ 综上，m的取值范围为[－1，＋∞).‎ 题型四　集合的新定义问题 例5　已知集合A＝{(x，y)|x2＋y2≤1，x，y∈Z}，B＝{(x，y)||x|≤2，|y|≤2，x，y∈Z}，定义集合AB＝{(x1＋x2，y1＋y2)|(x1，y1)∈A，(x2，y2)∈B}，则AB中元素的个数为________.‎ 答案　45‎ 解析　如图，集合A表示如图所示的所有圆点“”，集合B表示如图所示的所有圆点“”＋所有圆点“”，集合AB显然是集合{(x，y)||x|≤3，|y|≤3，x，y∈Z}中除去四个点{(－3，－3)，(－3，3)，(3，－3)，(3，3)}之外的所有整点(即横坐标与纵坐标都为整数的点)，即集合AB表示如图所示的所有圆点“”＋所有圆点“”＋所有圆点“”，共45个.故AB 中元素的个数为45.‎ 思维升华　解决以集合为背景的新定义问题，要抓住两点 ‎(1)紧扣新定义.首先分析新定义的特点，把新定义所叙述的问题的本质弄清楚，并能够应用到具体的解题过程之中，这是破解新定义型集合问题难点的关键所在；(2)用好集合的性质.解题时要善于从试题中发现可以使用集合性质的一些因素，在关键之处用好集合的运算与性质.‎ ‎　定义一种新的集合运算△：A△B＝{x|x∈A，且x∉B}.若集合A＝{x|x2－4x＋3<0}，B＝{x|2≤x≤4}，则按运算△，B△A＝____________.‎ 答案　{x|3≤x≤4}‎ 解析　A＝{x|10}，B＝{x|23}，‎ ‎∴∁UA＝{x|－1≤x≤3}，B＝{x|20}，若A⊆B，则实数c的取值范围是__________.‎ 答案　[1，＋∞)‎ 解析　由题意知，A＝{x|y＝lg(x－x2)}＝{x|x－x2>0}＝(0，1)，B＝{x|x2－cx<0，c>0}＝(0，c).由A⊆B，画出数轴，如图所示，得c≥1.‎ ‎8.(2015·浙江改编)已知集合P＝{x|x2－2x≥0}，Q＝{x|1＜x≤2}，则(∁RP)∩Q＝__________.‎ 答案　{x|11}，‎ 所以A∪B＝{x|x>1或x≤－1}.‎ ‎13.(2016·江苏无锡新区期中)设P、Q为两个非空实数集合，定义集合P*Q＝{z|z＝ab，a∈P，b∈Q}，若P＝{－1，0，1}，Q＝{－2，2}，则集合P*Q中元素的个数是________.‎ 答案　3‎ 解析　按P*Q的定义，P*Q中元素为2，－2，0，共3个.‎ ‎*14.设A是整数集的一个非空子集，对于k∈A，如果k－1∉A，且k＋1∉A，那么称k是A的一个“孤立元”.给定S＝{1，2，3，4，5，6，7，8}，由S的3个元素构成的所有集合中，不含“孤立元”的集合共有________个.‎ 答案　6‎ 解析　依题意可知，由S的3个元素构成的所有集合中，不含“孤立元”时，这三个元素一定是连续的三个自然数.故这样的集合共有6个.‎ ‎*15.已知集合A＝{x∈R||x＋2|<3}，集合B＝{x∈R|(x－m)(x－2)<0}，且A∩B＝(－1，n)，则m＝________，n＝________.‎ 答案　－1　1‎ 解析　A＝{x∈R||x＋2|<3}＝{x∈R|－5

查看更多