- 2021-06-16 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学人教a版必修四课时训练:1.2.1 任意角的三角函数(二)
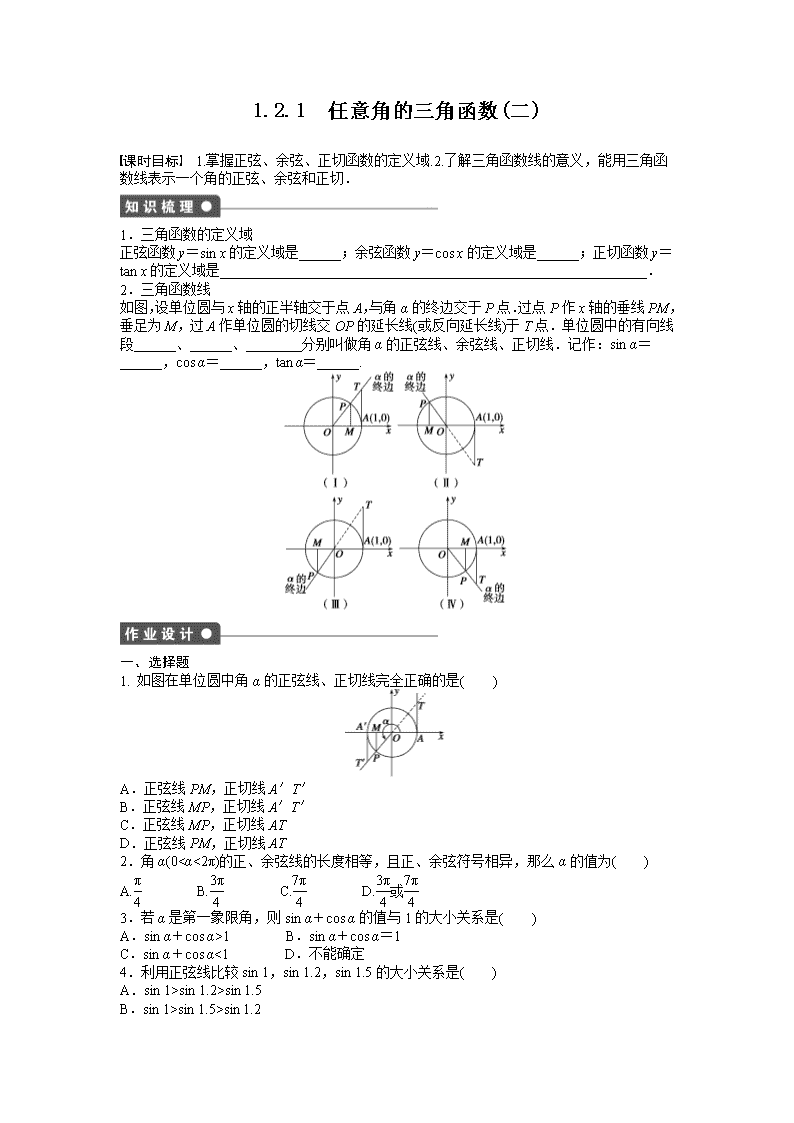
1.2.1 任意角的三角函数(二) 课时目标 1.掌握正弦、余弦、正切函数的定义域.2.了解三角函数线的意义,能用三角函 数线表示一个角的正弦、余弦和正切. 1.三角函数的定义域 正弦函数 y=sin x 的定义域是______;余弦函数 y=cos x 的定义域是______;正切函数 y= tan x 的定义域是_____________________________________________________________. 2.三角函数线 如图,设单位圆与 x 轴的正半轴交于点 A,与角α的终边交于 P 点.过点 P 作 x 轴的垂线 PM, 垂足为 M,过 A 作单位圆的切线交 OP 的延长线(或反向延长线)于 T 点.单位圆中的有向线 段______、______、________分别叫做角α的正弦线、余弦线、正切线.记作:sin α=______, cos α=______,tan α=______. 一、选择题 1. 如图在单位圆中角α的正弦线、正切线完全正确的是( ) A.正弦线 PM,正切线 A′T′ B.正弦线 MP,正切线 A′T′ C.正弦线 MP,正切线 AT D.正弦线 PM,正切线 AT 2.角α(0<α<2π)的正、余弦线的长度相等,且正、余弦符号相异,那么α的值为( ) A.π 4 B.3π 4 C.7π 4 D.3π 4 或7π 4 3.若α是第一象限角,则 sin α+cos α的值与 1 的大小关系是( ) A.sin α+cos α>1 B.sin α+cos α=1 C.sin α+cos α<1 D.不能确定 4.利用正弦线比较 sin 1,sin 1.2,sin 1.5 的大小关系是( ) A.sin 1>sin 1.2>sin 1.5 B.sin 1>sin 1.5>sin 1.2 C.sin 1.5>sin 1.2>sin 1 D.sin 1.2>sin 1>sin 1.5 5.若 0<α<2π,且 sin α< 3 2 ,cos α>1 2 ,则角α的取值范围是( ) A. -π 3 ,π 3 B. 0,π 3 C. 5π 3 ,2π D. 0,π 3 ∪ 5π 3 ,2π 6.如果π 4<α<π 2 ,那么下列不等式成立的是( ) A.cos α查看更多
相关文章
- 当前文档收益归属上传用户