2010-2011学年山东省济南市章丘一中高一(下)期中数学试卷
2010-2011学年山东省济南市章丘一中高一(下)期中数学试卷
一、选择题(共12小题,每小题4分,满分48分)
1. 赋值语句M=M+3表示的意义( )
A.将M的值赋给M+3 B.将M的值加3后再赋给M
C.M和M+3的值相等 D.以上说法都不对
2. A={x|−3
0)0(x=0)x(x−1)(x<0),则f(e)=( )
A.0 B.e(e−1) C.e D.e(e+1)
4. 在空间中下列结论中正确的个数是( )
①平行于同一直线的两直线平行;②垂直于同一直线的两直线平行;
③平行于同一平面的两直线平行;④垂直于同一平面的两直线平行.
A.1 B.2 C.3 D.4
5. 已知一个几何体它的主视图和左视图上都是一个长为4,宽为2的矩形,俯视图是一个半径为2的圆,则此几何体的表面积为( )
A.8π B.12π C.16π D.32π
6. 求过点P(3, 2),并与直线x+4y−2=0垂直的直线的方程为( )
A.x−4y−11=0 B.x+4y−11=0 C.4x+y−10=0 D.4x−y−10=0
7. 已知sinα=45,并且α是第二象限的角,那么tanα的值等于( )
A.−43 B.−34 C.34 D.43
8. 某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②.则完成①、②这两项调查宜采用的抽样方法依次是( )
A.分层抽样法,系统抽样法
B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法
D.简单随机抽样法,分层抽样法
9. 某校举行2010年元旦汇演,七位评委为某班的小品打出的分数茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
A.85,1.6 B.85,4 C.84,1.6 D.,4.84
10. 先后抛硬币两次,则至少一次正面朝上的概率是( )
A.14 B.13 C.34 D.23
11. 从装有2个红球和2个黒球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
A.至少有一个黒球与都是红球
B.至少有一个黒球与都是黒球
C.至少有一个黒球与至少有1个红球
D.恰有1个黒球与恰有2个黒球
12. 设有一个正方形网格,其中每个最小正方形的边长都等于6.现用直径等于2的硬币投掷到此网格上,则硬币落下后与格线有公共点的概率为( )
A.1636 B.2036 C.13 D.23
二、填空题(共4小题,每小题4分,满分16分)
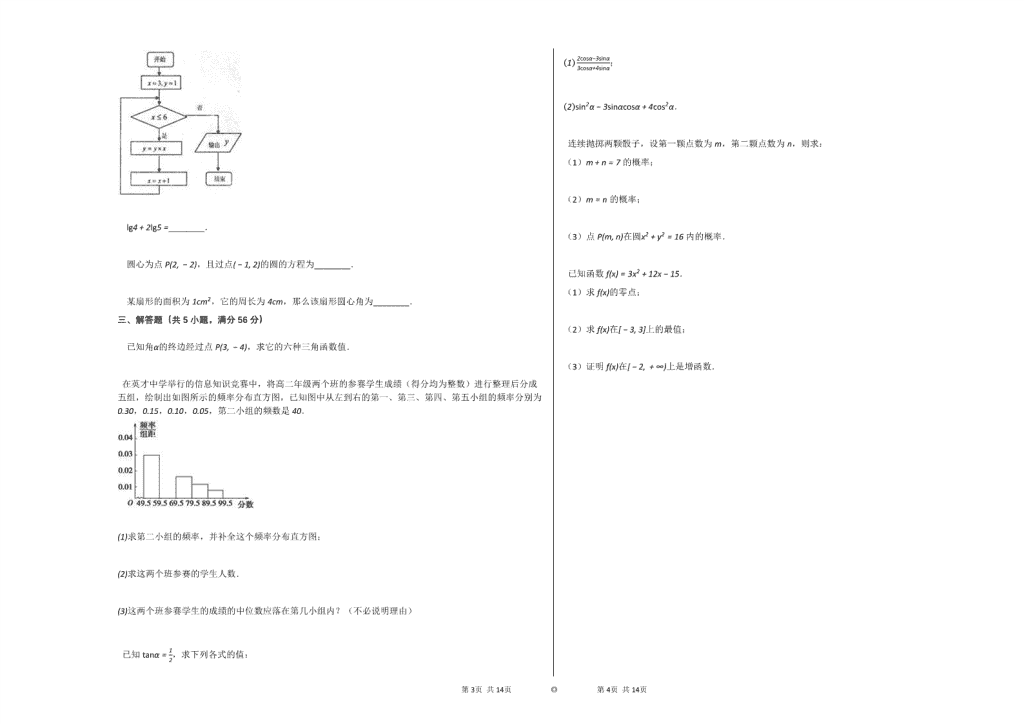
如图表示的程序所输出的结果是________.
第13页 共14页 ◎ 第14页 共14页
lg4+2lg5=________.
圆心为点P(2, −2),且过点(−1, 2)的圆的方程为________.
某扇形的面积为1cm2,它的周长为4cm,那么该扇形圆心角为________.
三、解答题(共5小题,满分56分)
已知角α的终边经过点P(3, −4),求它的六种三角函数值.
在英才中学举行的信息知识竞赛中,将高二年级两个班的参赛学生成绩(得分均为整数)进行整理后分成五组,绘制出如图所示的频率分布直方图,已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05,第二小组的频数是40.
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数.
(3)这两个班参赛学生的成绩的中位数应落在第几小组内?(不必说明理由)
已知tanα=12,求下列各式的值:
12cosα−3sinα3cosα+4sinα;
2sin2α−3sinαcosα+4cos2α.
连续抛掷两颗骰子,设第一颗点数为m,第二颗点数为n,则求:
(1)m+n=7的概率;
(2)m=n的概率;
(3)点P(m, n)在圆x2+y2=16内的概率.
已知函数f(x)=3x2+12x−15.
(1)求f(x)的零点;
(2)求f(x)在[−3, 3]上的最值;
(3)证明f(x)在[−2, +∞)上是增函数.
第13页 共14页 ◎ 第14页 共14页
参考答案与试题解析
2010-2011学年山东省济南市章丘一中高一(下)期中数学试卷
一、选择题(共12小题,每小题4分,满分48分)
1.
【答案】
B
【考点】
赋值语句
【解析】
根据赋值语句的作用是将表达式所代表的值赋给变量,进行判定即可.
【解答】
解:赋值语句的一般格式:变量=表达式赋值语句中的“=”称作赋值号
赋值语句的作用是将表达式所代表的值赋给变量;
故选B
2.
【答案】
D
【考点】
并集及其运算
【解析】
分别把两集合的解集表示在数轴上,根据数轴求出两集合的并集即可.
【解答】
解:把集合A={x|−30)0(x=0)x(x−1)(x<0),
因为e>0,
所以f(e)=e(e+1).
故选D.
4.
【答案】
B
【考点】
空间中直线与直线之间的位置关系
【解析】
结合公理及正方体模型可以判断:①④正确,②③错误,可以利用反证法证明结论,也可以从具体的实物模型中去寻找反例证明.
【解答】
解:①④正确,②③错误
①:根据公理4可知:平行具有传递性,即如果a // b,a // c,那么b // c,所以①正确;
②:如图1所示:在正方体AC1中,D1A1⊥A1A,B1A1⊥A1A,但是D1A1∩B1A1=A1,所以②错误;
③:如图1所示:A1C1 // 平面ABCD,B1D1 // 平面ABCD,但是A1C1与B1D1相交,所以③错误;
④:如图2所示:假设a⊥α,b⊥α,且a∩b=A,则过一点有两条直线均垂直于平面α,故假设错误,所以④正确.
故选B.
5.
【答案】
C
【考点】
由三视图求表面积
【解析】
由已知中三视图我们可以确定,该几何体是以母线长为2,底面半径为2的圆柱,即可求得结果.
【解答】
解:根据题意知该几何体是母线长为2,底面半径为2的圆柱
因此它的表面积为8π+2×4π=16π
故选C.
6.
【答案】
D
第13页 共14页 ◎ 第14页 共14页
【考点】
两条直线垂直与倾斜角、斜率的关系
【解析】
设与直线x+4y−2=0垂直的直线的方程为 4x−y+m=0,把点P(3, 2)代入可得m值,即得所求的直线方程.
【解答】
解:设 与直线x+4y−2=0垂直的直线的方程为 4x−y+m=0,把点P(3, 2)代入可得,12−2+m=0,
∴ m=−10,故所求的直线方程为 4x−y−10=0,故选 D.
7.
【答案】
A
【考点】
同角三角函数基本关系的运用
象限角、轴线角
【解析】
由角的正弦值和角所在的象限,求出角的余弦值,然后,正弦值除以余弦值得正切值.
【解答】
解:∵ sinα=45且α是第二象限的角,
∴ cosα=−35,
∴ tanα=−43.
故选A.
8.
【答案】
B
【考点】
分层抽样方法
系统抽样方法
简单随机抽样
【解析】
此题为抽样方法的选取问题.当总体中个体较少时宜采用简单随机抽样法;当总体中的个体差异较大时,宜采用分层抽样;当总体中个体较多时,宜采用系统抽样.
【解答】
解:依据题意,第①项调查中,总体中的个体差异较大,应采用分层抽样法;
第②项调查总体中个体较少,应采用简单随机抽样法.
故选B.
9.
【答案】
A
【考点】
极差、方差与标准差
众数、中位数、平均数
【解析】
由已知中的茎叶图,我们可以得到七位评委为某班的小品打出的分数,及去掉一个最高分和一个最低分后的数据,代入平均数公式及方差公式,即可得到所剩数据的平均数和方差.
【解答】
解:由已知的茎叶图七位评委为某班的小品打出的分数为:
79,84,84,86,84,87,93
去掉一个最高分93和一个最低分79后,
所剩数据的平均数x¯=84+84+86+84+875=85
方差S2=15[(84−85)2+(84−85)2+(86−85)2+(84−85)2+(87−85)2]=1.6
故选A.
10.
【答案】
C
【考点】
古典概型及其概率计算公式
【解析】
由题意此事件为古典概型的随机事件的概率问题,又由于先后抛硬币两次所以事件空间的总数利用排列组合可知为4种;而在两次抛掷的结果中至少一次正面朝上的总数为3种,利用古典概型随机事件的概率公式即可求解.
【解答】
解:由题意得:基本事件为(正,反),(正,正),(反,正),(反,反),共4种.
至少一次正面朝上的基本事件为:(正,反),(反,正),(反,反),共3种.
所以至少一次正面朝上的概率为34.
故选C.
11.
【答案】
D
【考点】
互斥事件与对立事件
【解析】
互斥事件是两个事件不包括共同的事件,对立事件首先是互斥事件,再就是两个事件的和事件是全集,由此规律对四个选项逐一验证即可得到答案.
【解答】
解:A中的两个事件是对立事件,故不符合要求;
B中的两个事件是包含关系,不是互斥事件,故不符合要求;
C中的两个事件都包含一个黑球一个红球的事件,不是互斥关系;
D中的两个事件是互互斥且不对立的关系,故正确.
故选D
12.
【答案】
第13页 共14页 ◎ 第14页 共14页
B
【考点】
几何概型计算(与长度、角度、面积、体积有关的几何概型)
【解析】
因为硬币的直径是2,所以半径是1.当硬币的圆心落在网格小正方形的中心(边长为4的小正方形内)是不会与格线相交的即不相交的概率是4×46×6,由此能求出与格线有公共点的概率.
【解答】
解:因为硬币的直径是2,所以半径是1.
当硬币的圆心落在网格小正方形的中心(边长为4的小正方形内)
是不会与格线相交的
即不相交的概率是4×46×6,
所以与格线有公共点的概率是1−4×46×6=2036,
故选B.
二、填空题(共4小题,每小题4分,满分16分)
【答案】
360
【考点】
循环结构的应用
【解析】
分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出y=3×4×5×6的值,并输出.
【解答】
解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是
计算并输出y=3×4×5×6的值
∵ y=3×4×5×6=360.
故答案为:360.
【答案】
2
【考点】
对数的运算性质
【解析】
根据对数的性质,把2lg5写成lg25,再用对数的计算性质,变化成一个对数形式,得到结果.
【解答】
解:lg4+2lg5=lg4+lg25=lg100=2
故答案为:2.
【答案】
(x−2)2+(y+2)2=25
【考点】
圆的标准方程
【解析】
利用两点间的距离公式求出半径,根据圆心坐标写出圆的标准方程.
【解答】
解:半径等于(−1−2)2+(2+2)2=5,故圆的方程为 (x−2)2+(y+2)2=25,
故答案为(x−2)2+(y+2)2=25.
【答案】
2(rad)
【考点】
扇形面积公式
【解析】
设该扇形圆心角为θ,半径为r,由题意得12θr2=1,2r+θr=4,解方程求得θ 值.
【解答】
设该扇形圆心角为θ,半径为r,
则由题意得12θr2=1,2r+θr=4,
∴ 12θr2=12r⋅θr=12r(4−2r)=1,∴ r=1,∴ θ=2 (rad),
三、解答题(共5小题,满分56分)
【答案】
解:由题意可得x=3,y=−4,r=5,根据三角函数的定义可得
sinα=yr=−45,cosα=xr=35,tanα=yx=−43,
cotα=xy=−34,secα=rx=53,cscα=ry=−54.
【考点】
三角函数
【解析】
由题意可得x=3,y=−4,r=5,根据三角函数的定义可得 它的六种三角函数值.
【解答】
解:由题意可得x=3,y=−4,r=5,根据三角函数的定义可得
sinα=yr=−45,cosα=xr=35,tanα=yx=−43,
cotα=xy=−34,secα=rx=53,cscα=ry=−54.
【答案】
第13页 共14页 ◎ 第14页 共14页
解:(1)∵ 第一、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05
各组频率和为1,
∴ 第二小组的频率为1−(0.30+0.15+0.10+0.05)=0.4;
频率分布直方图如下图所示:
(2)∵ 第二小组的频数是40,
由(1)得第二小组的频率为0.4;
则40÷0.4=100;
即这两个班参赛的学生人数为100.
(3)中位数落在第二小组内.
【考点】
频率分布直方图
用样本的频率分布估计总体分布
【解析】
(1)由已知中第一、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05,各小组频率和为1,可以求出第二小组的频率.
(2)由第二组的频率及频数,根据频率=频数÷样本容量,即可求出样本容量即两个班参赛的学生人数.
(3)根据中位数的定义,由第一、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05,易判断中位数应落在第几小组内.
【解答】
解:(1)∵ 第一、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05
各组频率和为1,
∴ 第二小组的频率为1−(0.30+0.15+0.10+0.05)=0.4;
频率分布直方图如下图所示:
(2)∵ 第二小组的频数是40,
由(1)得第二小组的频率为0.4;
则40÷0.4=100;
即这两个班参赛的学生人数为100.
(3)中位数落在第二小组内.
【答案】
解:1将分子和分母同时除以cosα,
原式=2−3tanα3+4tanα=110.
2原式=sin2α−3sinαcosα+4cos2αsin2α+cos2α
=tan2α−3tanα+4tan2+1
=115.
【考点】
三角函数的化简求值
【解析】
(1)将分子和分母同时除以cosα,把tanα的值代入即可求得答案.
(2)利用sin2α+cos2α=1,原式除以sin2α+cos2α,分子分母同时除以sin2α,进而把tanα的值代入即可求得答案.
【解答】
解:1将分子和分母同时除以cosα,
原式=2−3tanα3+4tanα=110.
2原式=sin2α−3sinαcosα+4cos2αsin2α+cos2α
=tan2α−3tanα+4tan2+1
=115.
【答案】
解:共有6×6=36个基本事件,(1)记“m+n=7”为事件A,则A包含6个基本事件,,(1, 6),(2, 5),(3, 4),(4, 3),(5, 2),(6, 1).
故P(A)=636=16;
(2)记“m=n”为事件B,则B包含6个基本事件,(1, 1),(2, 2),(3, 3),(4, 4),(5, 5),(6, 6),故P(B)=636=16;
(3)记“点P(m, n)在圆x2+y2=16内”为事件C,则C包含8个基本事件,(1, 1),(1, 2),(1, 3),
(2, 1)(2, 2),(2, 3),(3, 1),(3, 2). 故P(C)=836=29.
【考点】
列举法计算基本事件数及事件发生的概率
【解析】
共有6×6=36个基本事件,(1)记“m+n=7”为事件A,则A包含6个基本事件,故P(A)=636=16.
(2)记“m=n”为事件B,则B包含6个基本事件,故P(B)=636=16.
(3)记“点P(m, n)在圆x2+y2=16内”为事件C,则C包含8个基本事件,故P(C)=836=29.
【解答】
解:共有6×6=36个基本事件,(1)记“m+n=7”为事件A,则A包含6个基本事件,,(1, 6),(2, 5),(3, 4),(4, 3),(5, 2),(6, 1).
故P(A)=636=16;
第13页 共14页 ◎ 第14页 共14页
(2)记“m=n”为事件B,则B包含6个基本事件,(1, 1),(2, 2),(3, 3),(4, 4),(5, 5),(6, 6),故P(B)=636=16;
(3)记“点P(m, n)在圆x2+y2=16内”为事件C,则C包含8个基本事件,(1, 1),(1, 2),(1, 3),
(2, 1)(2, 2),(2, 3),(3, 1),(3, 2). 故P(C)=836=29.
【答案】
解:(1)令f(x)=3x2+12x−15=0
得:x=−5或x=1
∴ f(x)的零点为−5,1.
(2)f(x)=3x2+12x−15=3(x2+4x−5)=3(x+2)2−27,
f(x)对称轴为x=−2,
∴ f(x)在[−3, 3]上的最小值为f(−2)=−27,
最大值为f(3)=48;
(3)设x1,x2∈[−2, +∞)且x1<x2
则f(x2)−f(x1)=3(x22−x21)+12(x2−x1)
=3(x2−x1)(x2+x1+4)
∵ x1,x2∈[−2, +∞)且x1<x2
∴ x2−x1>0,x2+x1+4>0
∴ 3(x2−x1)(x2+x1+4)>0
∴ f(x2)−f(x1)>0
∴ f(x)在[−2, +∞)上是增函数.
【考点】
二次函数在闭区间上的最值
二次函数的性质
【解析】
(1)求零点时使f(x)=3x2+12x−15=0即可
(2)二次函数定区间上求最值主要看对称轴与区间端点的关系
(3)可以用函数单调性的定义判断函数的单调性.
【解答】
解:(1)令f(x)=3x2+12x−15=0
得:x=−5或x=1
∴ f(x)的零点为−5,1.
(2)f(x)=3x2+12x−15=3(x2+4x−5)=3(x+2)2−27,
f(x)对称轴为x=−2,
∴ f(x)在[−3, 3]上的最小值为f(−2)=−27,
最大值为f(3)=48;
(3)设x1,x2∈[−2, +∞)且x1<x2
则f(x2)−f(x1)=3(x22−x21)+12(x2−x1)
=3(x2−x1)(x2+x1+4)
∵ x1,x2∈[−2, +∞)且x1<x2
∴ x2−x1>0,x2+x1+4>0
∴ 3(x2−x1)(x2+x1+4)>0
∴ f(x2)−f(x1)>0
∴ f(x)在[−2, +∞)上是增函数.
第13页 共14页 ◎ 第14页 共14页