优秀导学案映射_()

优秀导学案映射_()

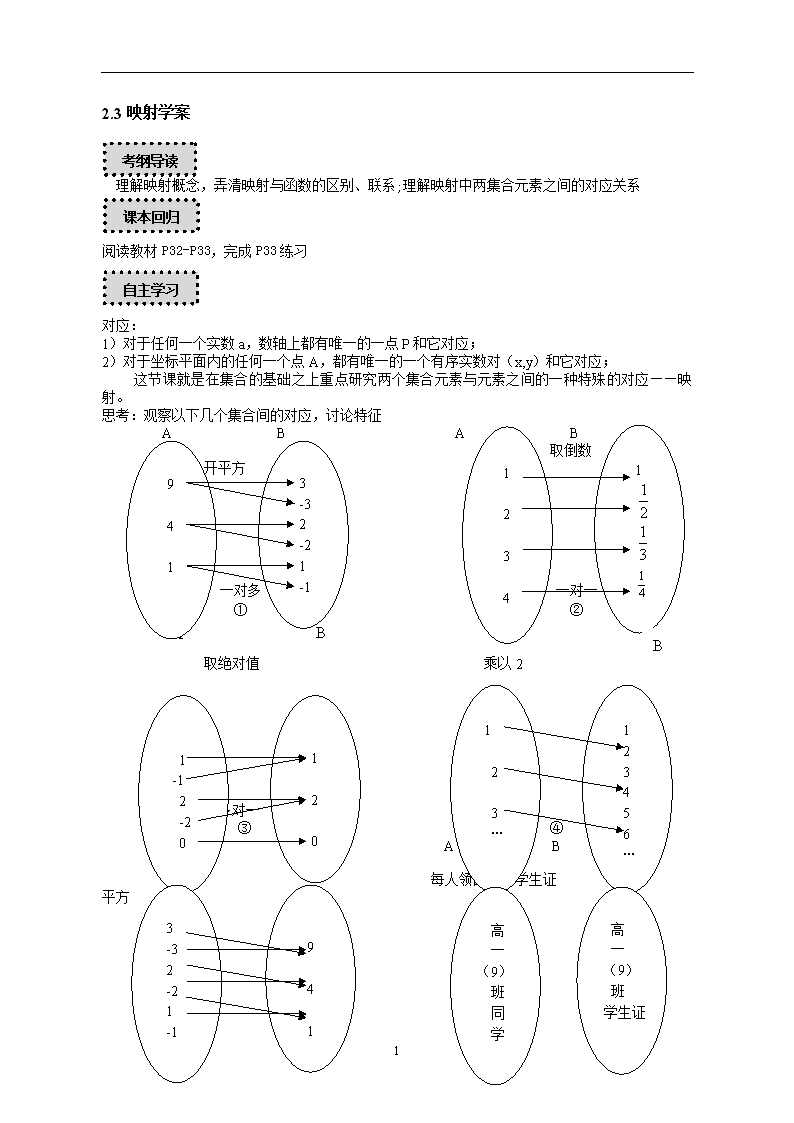
‎ ‎ ‎2.3映射学案 考纲导读 ‎ 理解映射概念，弄清映射与函数的区别、联系;理解映射中两集合元素之间的对应关系 课本回归 阅读教材P32-P33，完成P33练习 自主学习 对应：‎ ‎1）对于任何一个实数a，数轴上都有唯一的一点P和它对应；‎ ‎2）对于坐标平面内的任何一个点A，都有唯一的一个有序实数对（x,y）和它对应；‎ 这节课就是在集合的基础之上重点研究两个集合元素与元素之间的一种特殊的对应——映射。‎ 思考：观察以下几个集合间的对应，讨论特征 ‎ 1‎ ‎ 2‎ ‎ 3‎ ‎ 4‎ ‎1‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ A B A B 取倒数‎ 9‎ ‎ ‎ ‎ 4‎ ‎ 1‎ ‎3‎ ‎-3‎ ‎2‎ ‎-2‎ ‎1‎ ‎-1‎ ‎ 开平方 ‎ 一对一 ‎②‎ 一对多 ‎ ①‎ ‎ ‎ ‎ ‎ B A A ‎ ‎ B ‎ 取绝对值 乘以2‎ ‎ 1‎ ‎ 2‎ ‎ 3‎ ‎ …‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎…‎ ‎ ‎ ‎ 1‎ ‎-1 ‎ ‎ 2‎ ‎-2‎ ‎ 0‎ ‎ ‎ ‎1‎ ‎2‎ ‎0‎ ‎ 多对一 一对一 ③ ‎④‎ ‎ A B A B ‎ 高 ‎ 一 ‎ （9）‎ ‎ 班 ‎ 同 ‎ 学 高 ‎ 一 ‎ （9）‎ ‎ 班 ‎ 学生证 ‎ 每人领自己的学生证 ‎ 3‎ ‎ -3‎ ‎ 2‎ ‎ -2‎ ‎ 1‎ ‎ -1‎ ‎9‎ ‎4‎ ‎1‎ 平方 4‎ ‎ ‎ ‎ ‎ ‎ 多对一 一对一 ‎ ⑤ ‎ ‎ ⑥‎ 定义：一般地，设Ａ、Ｂ是两个集合，若按照某种对应法则f，对于集合Ａ中的任何一个元素，在集合Ｂ中都有唯一的元素和它对应，则这样的对应叫做集合Ａ到集合Ｂ的映射，记作f：A→B。‎ 问题探究 ‎【例题1】判断下列对应是否是从集合A到集合B的映射 ‎①、A=R，B=｛x|x＞0 且x∈R｝,f：x→y=|x|‎ ‎【例题2】设A=｛a、b｝,B=｛c、d｝‎ ‎①用图示法表示集合A到集合B的所有不同映射；‎ ‎②若B=｛c、d、e｝,则A到B可建立多少个不同映射；‎ 课堂训练 说说下列对应关系是否为映射。‎ ‎①A=｛，1，-2｝，B=｛3，2，1，，0｝ f：x→y=+1,x∈A,y∈B ‎②A=R，B=R，f：x→y=2x+1, x∈A,y∈B ‎③A=N*,B=｛0,1｝, f：除以2的余数 ‎④A=｛某商场的所有商品｝B=｛商品的价格｝f：每种商品对自己的价格 ‎ 练 案 ‎2.3映射 高一数学（）‎ 姓名：____________‎ 班级：____________‎ 第一组 ‎1.关于，下列说法错误的是 （ ）‎ A.A集合中的每个元素在B集合中都存在元素与之对应；‎ 4‎ ‎ ‎ B.“在B集合中存在唯一元素和A集合中元素对应”即A中的元素不能对应B集合中一个以上的元素；‎ C.A集合中可以有两个或两个以上的元素对应B集合中的一个元素；‎ D.B集合中不可以有元素不被A集合中的元素所对应；‎ ‎2.下列从集合A到集合B的对应中为映射的是（ ）‎ A、‎ B、‎ C、‎ D、‎ ‎3.已知集合不表示P到Q的映射的是（ ）‎ A、 B、 C、 D、‎ ‎4.给定映射 ‎5.已知从A到B的映射是从到的映射______‎ ‎6.判断下列对应是否为A集合到B集合的映射和一一映射？‎ ‎（1）；‎ ‎（2）；‎ ‎（3）；‎ ‎（4）‎ 第二组 ‎7.在给定的映射的条件下，点的原象是（ ）‎ A、 B、或 ‎ ‎ C、 D、‎ ‎8.映射定义域A到值域B上的函数，下列结论正确的是（ ）‎ A、A中每个元素必有象，但B中元素不一定由原象；‎ 4‎ ‎ ‎ B、B中元素必有原象，‎ C、B中元素只有一个原象;‎ D、A或B可以空集或不是数集；‎ ‎9.已知到自身的映射，则这样的映射有多少个？若是一一映射，即这样的一一映射有多少个？‎ 第三组 ‎10.‎ 4‎