黑龙江省双鸭山市第一中学2019-2020学年高一线上考试数学试卷

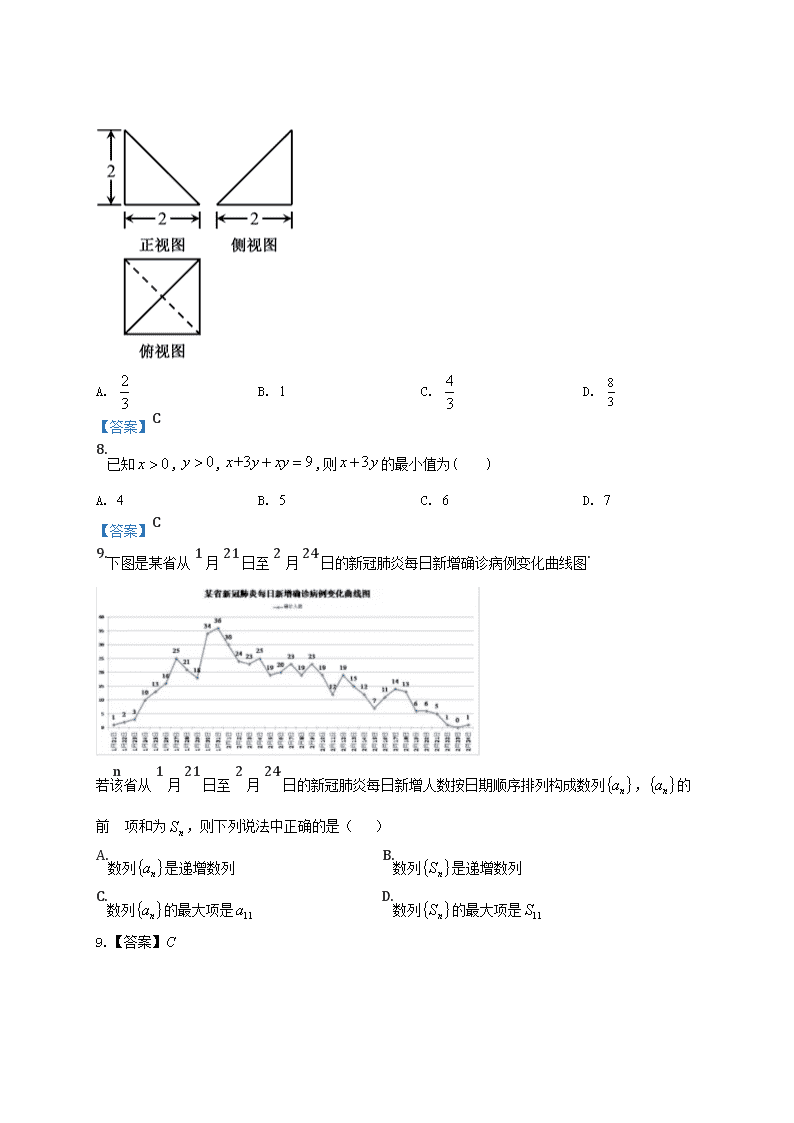
黑龙江省双鸭山市第一中学2019-2020学年高一线上考试数学试卷

数学试题 ‎1.若，则下列不等式成立的是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎2.设等比数列的公比，前n项和为，则（ ）‎ A. B. C. 2 D. 4‎ ‎【答案】A ‎3.已知正四棱锥的顶点均在球上，且该正四棱锥的各个棱长均为，则球的表面积为(　　)‎ A B. C. D. ‎ ‎【答案】C ‎4.已知向量, ,且,则=( )‎ A. 5 B. C. D. 10‎ ‎【答案】B ‎5.不等式的解集为,则的值为(   )‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎6.在△ABC中，.则△ABC—定是（）.‎ A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 形状不确定 ‎【答案】A ‎7.某几何体三视图如图所示，则此几何体的体积为（ ）‎ A. B. 1 C. D. ‎ ‎【答案】C ‎8.已知,,,则的最小值为( )‎ A. 4 B. 5 C. 6 D. 7‎ ‎【答案】C ‎9.下图是某省从‎1月21日至‎2月24日的新冠肺炎每日新增确诊病例变化曲线图.‎ 若该省从1月21日至2月24日的新冠肺炎每日新增人数按日期顺序排列构成数列，的前n项和为，则下列说法中正确的是（ ）‎ A.数列是递增数列 B.数列是递增数列 C.数列的最大项是 D.数列的最大项是 ‎9.【答案】C ‎10．已知数列的前项和为，且.若数列为递增数列，则实数的取值范围为（ ）‎ A． B． C． D．‎ ‎10．B ‎11.在中,角所对的边分别是,且,若的面积为,则的最小值为( )‎ A. B. C. D. ‎ ‎【答案】B ‎12.设等差数列的前项的和为，等差数列的前项的和为，且满足.若存在正整数使得，则的最大值为（ ）‎ A. 3 B. 4 C. 6 D. 8‎ ‎【答案】B 故选:B ‎13.与的等比中项是______.‎ ‎【答案】‎ ‎14.‎ ‎15.已知△A′B′C′是水平放置的边长为的正三角形ABC的斜二测水平直观图，那么△A′B′C′的面积为_________．‎ ‎．在图乙中作C′D′⊥A′B′于D′，则．所以．故填 ‎16．（2）（4）‎ ‎17、（10分）‎ ‎18.等差数列中，，．‎ ‎（1）求数列的通项公式；‎ ‎（2）设，求的值．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎（Ⅰ）设等差数列的公差为．‎ 由已知得，‎ 解得．‎ 所以．‎ ‎（Ⅱ）由（Ⅰ）可得．‎ 所以 ‎．‎ 考点：1、等差数列通项公式；2、分组求和法．‎ ‎19.已知中，.‎ ‎（1）求边的长；‎ ‎（2）若边的中点为，求中线的长.‎ ‎19.（1） （2）‎ ‎20.学案册上的(1)a=b=2,(2)‎ ‎21.已知数列的前项和为,且有, ,‎ ‎（1）求数列的通项公式;‎ ‎（2）若 ,求数列的前项和 .‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ 试题分析：(1)已知，所以得到，‎ ‎；（2），，错位相减求和；‎ ‎（1）由题意知 ‎ ‎∴ , ,又∵,∴是以2为首项,2为公比的等比数列.‎ ‎∴‎ ‎（2）由已知得, ，‎ ‎ ，‎ 两式相减,得 ‎ 所以得到．‎ ‎22.已知定义在上的函数满足，且对于任意的，都有，数列满足，.‎ ‎（1）令，求数列的通项公式；‎ ‎（2）令，，为数列的前项和，求证：.‎ ‎【答案】（1），.（2）见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）先令,可得,再由可得数列是首项为4,公比为2的等比数列,进而求解；‎ ‎（2）由（1）,则,则,进而利用裂项相消法求证即可.‎ ‎【详解】解:（1）令,则,所以,‎ 因为,‎ 所以,所以数列为公比为2的等比数列,‎ 首项为,‎ 所以,则,.‎ ‎（2）由（1）,,‎ 则,‎ 所以.‎ ‎【点睛】本题考查构造法求数列的通项公式,考查裂项相消法求数列的和,考查证明数列的不等式.‎