高考数学一轮复习精品题集之函数
函数
必修 1 第 2 章 函数概念与基本初等函数Ⅰ
§2.1.1 函数的概念和图象
重难点:在对应的基础上理解函数的概念并能理解符号“y=f(x)”的含义,掌握函数定义
域与值域的求法; 函数的三种不同表示的相互间转化,函数的解析式的表示,理解和表示
分段函数;函数的作图及如何选点作图,映射的概念的理解.
考纲要求:①了解构成函数的要素,会求一些简单函数的定义域和值域;
②在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函
数;
③了解简单的分段函数,并能简单应用;
经典例题:设函数 f(x)的定义域为[0,1],求下列函数的定义域:
(1)H(x)=f(x2+1);
(2)G(x)=f(x+m)+f(x-m)( m>0).
当堂练习:w.w.w.g.k.x.x.c.o.m
1. 下列四组函数中,表示同一函数的是( )
A.
2( ) , ( )f x x g x x B.
2( ) , ( ) ( )f x x g x x
C.
2 1( ) , ( ) 1
1
xf x g x x
x
D.
2( ) 1 1, ( ) 1f x x x g x x
2 函数 ()y f x 的图象与直线 xa 交点的个数为( )
A.必有一个 B.1 个或 2 个 C.至多一个 D.可能 2 个以上
3.已知函数
1()
1
fx
x
,则函数 [ ( )]f f x 的定义域是( )
A. 1xx B. 2xx C. 1, 2xx D. 1, 2xx
4.函数
1()
1 (1 )
fx
xx
的值域是( )
A.
5[ , )
4
B.
5( , ]
4
C.
4[ , )
3
D.
4( , ]
3
5.对某种产品市场产销量情况如图所示,其中: 1l 表示产品各年年
产量的变化规律; 2l 表示产品各年的销售情况.下列叙述: ( )
(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;
(2)产品已经出现了供大于求的情况,价格将趋跌;
(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;
(4)产品的产、销情况均以一定的年增长率递增.你认为较合理的是( )
A.( 1),(2),(3) B.( 1),(3),(4) C.( 2),( 4) D.( 2),( 3)
6.在对应法则 , , ,x y y x b x R y R 中,若 25 ,则 2 , 6.
7 .函数 ()fx 对 任 何 xR 恒有 1 2 1 2( ) ( ) ( )f x x f x f x , 已 知 (8) 3f ,则
( 2)f .
8.规定记号“ ”表示一种运算,即 a b a b a b a b R ,、 . 若13k,则函数
f x k x的值域是___________.
9.已知二次函数 f(x)同时满足条件: (1) 对称轴是 x=1; (2) f(x)的最大值为 15;(3) f(x)
的两根立方和等于 17.则 f(x)的解析式是 .
10.函数 2
5
22
y
xx
的值域是 .
11. 求下列函数的定义域 : (1)
() 12
1
xfx
x
(2)
0( 1)() xfx
xx
12.求函数 32y x x 的值域.
13.已知 f(x)=x2+4x+3,求 f(x)在区间[t,t+1]上的最小值 g(t)和最大值 h(t).
14.在边长为 2 的正方形 ABCD 的边上有动点 M,从点 B
开始,沿折线 BCDA 向 A 点运动,设 M 点运动的距离为 x,
△ABM 的面积为 S.
(1)求函数 S=的解析式、定义域和值域;
(2)求 f[f(3)]的值.
必修 1 第 2 章 函数概念与基本初等函数Ⅰ
A B
C D
§2.1.2 函数的简单性质
重难点:领会函数单调性的实质,明确单调性是一个局部概念,并能利用函数单调性的定义
证明具体函数的单调性,领会函数最值的实质,明确它是一个整体概念,学会利用函数的单
调性求最值;函数奇偶性概念及函数奇偶性的判定;函数奇偶性与单调性的综合应用和抽象
函数的奇偶性、单调性的理解和应用;了解映射概念的理解并能区别函数和映射.
考纲要求:①理解函数的单调性、最大(小)值及其几何意义;结合具体函数,了解函数奇
偶性的含义;并了解映射的概念;
②会运用函数图像理解和研究函数的性质.
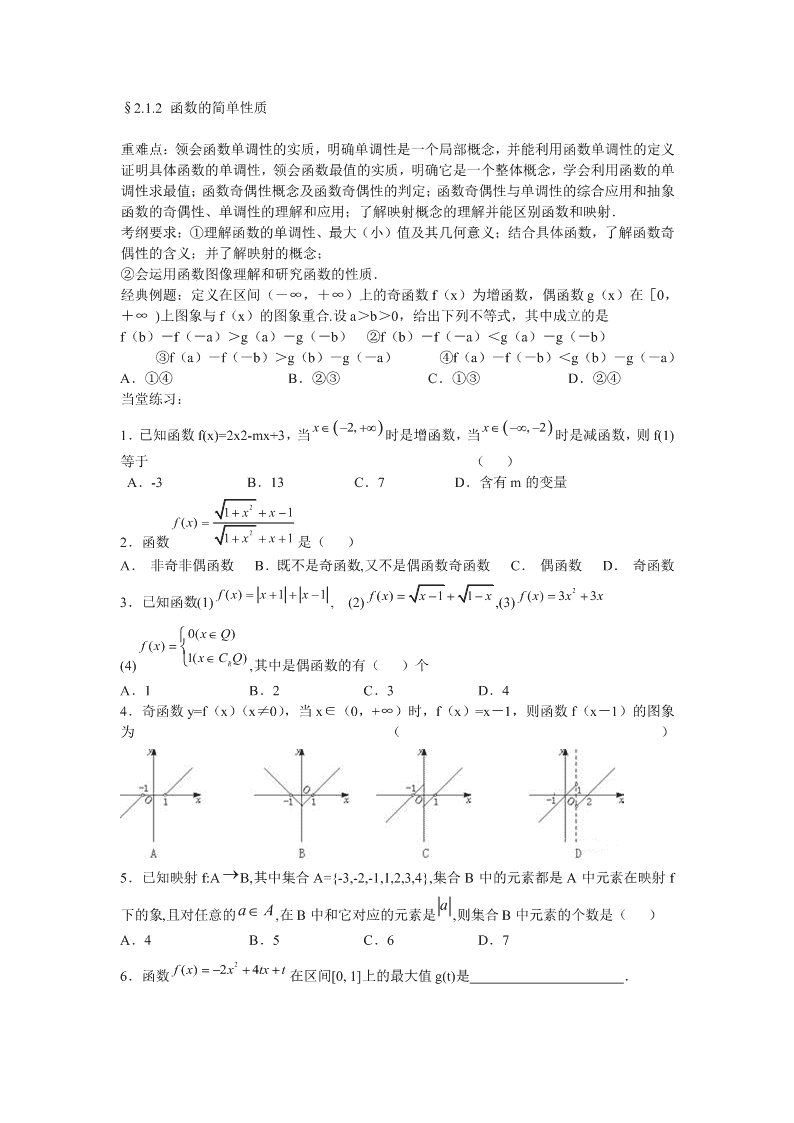
经典例题:定义在区间(-∞,+∞)上的奇函数 f(x)为增函数,偶函数 g(x)在[0,
+∞ )上图象与 f(x)的图象重合.设 a>b>0,给出下列不等式,其中成立的是
f(b)-f(-a)>g(a)-g(-b) ②f(b)-f(-a)<g(a)-g(-b)
③f(a)-f(-b)>g(b)-g(-a) ④f(a)-f(-b)<g(b)-g(-a)
A.①④ B.②③ C.①③ D.②④
当堂练习:
1.已知函数 f(x)=2x2-mx+3,当 2,x 时是增函数,当 ,2x 时是减函数,则 f(1)
等于 ( )
A.-3 B.13 C.7 D.含有 m 的变量
2.函数
2
2
11()
11
xxfx
xx
是( )
A. 非奇非偶函数 B.既不是奇函数,又不是偶函数奇函数 C. 偶函数 D. 奇函数
3.已知函数(1) ( ) 1 1f x x x , (2) ( ) 1 1f x x x ,(3)
2( ) 3 3f x x x
(4)
0( )
()
1( )R
xQ
fx
x C Q
,其中是偶函数的有( )个
A.1 B.2 C.3 D.4
4.奇函数 y=f(x)( x≠0),当 x∈(0,+∞)时,f(x)=x-1,则函数 f(x-1)的图象
为 ( )
5.已知映射 f:A B,其中集合 A={-3,-2,-1,1,2,3,4},集合 B 中的元素都是 A 中元素在映射 f
下的象,且对任意的 Aa ,在 B 中和它对应的元素是 a ,则集合 B 中元素的个数是( )
A.4 B.5 C.6 D.7
6.函数
2( ) 2 4f x x tx t 在区间[0, 1]上的最大值 g(t)是 .
7 . 已 知 函 数 f(x) 在 区 间 (0, ) 上 是 减 函 数 , 则
2( 1)f x x 与
()
3
4
f
的 大 小 关 系
是 .
8.已知 f(x)是定义域为 R 的偶函数,当 x<0 时, f(x)是增函数,若 x1<0,x2>0,且 12xx ,则 1()fx
和 2()fx 的大小关系是 .
9.如果函数 y=f(x+1)是偶函数,那么函数 y=f(x)的图象关于_________对称.
10.点(x,y)在映射 f 作用下的对应点是
33( , )
22
x y y x
,若点 A 在 f 作用下的对应点是
B(2,0),则点 A 坐标是 .
13. 已知函数
2 12
2()
xx
fx
x
,其中 [1, )x ,(1)试判断它的单调性;(2)试求它的最小值.
14.已知函数
2
2 1 1() afx
a a x
,常数 0a 。
(1)设 0mn,证明:函数 ()fx在[]mn, 上单调递增;
(2)设 0 mn且 ()fx的定义域和值域都是[]mn, ,求 nm 的最大值.
13.(1)设 f(x)的定义域为 R 的函数,求证:
1( ) [ ( ) ( )]
2
F x f x f x
是偶函数;
1( ) [ ( ) ( )]
2
G x f x f x
是奇函数.
(2)利用上述结论,你能把函数
32( ) 3 2 3f x x x x 表示成一个偶函数与一个奇函数之和的
形式.
14. 在集合 R 上的映射:
2
1 :1f x z x ,
2
2 : 4( 1) 1f z y z .
(1)试求映射 :f x y 的解析式;
(2)分别求函数 f1(x)和 f2(z)的单调区间;
(3) 求函数 f(x)的单调区间.
必修 1 第 2 章 函数概念与基本初等函数Ⅰ
§2.1.3 单元测试
1. 设集合 P= 04xx ,Q= 02yy ,由以下列对应 f 中不能构成 A 到 B 的映射的是
( )A.
1
2
yx
B.
1
3
yx
C.
2
3
yx
D.
1
8
xy
2.下列四个函数: (1)y=x+1; (2)y=x+1; (3)y=x2-1; (4)y=
1
x ,其中定义域与值域相同的是
( ) A.(1)(2) B.(1)(2)(3) C.2)(3) D.(2)(3)(4)
3.已知函数
7( ) 2cf x ax bx
x
,若 (2006) 10f ,则 ( 2006)f 的值为( )
A.10 B. -10 C.-14 D.无法确定
4.设函数
1( 0)
()
1 ( 0)
x
fx
x
,则
( ) ( ) ( ) ()
2
a b a b f a b ab
的值为( )
A.a B.b C.a、b 中较小的数 D.a、b 中较大
的数
5.已知矩形的周长为 1,它的面积 S 与矩形的长 x 之间的函数关系中,定义域为( )
A. 10
4
xx
B. 10
2
xx
C. 11
42
xx
D. 1 1
4
xx
6.已知函数 y=x2-2x+3 在[0,a](a>0)上最大值是 3,最小值是 2,则实数 a 的取值范围是( )
A.0
f(-1) B.f(-1)>f(-2) C.f(1)>f(2) D.f(-2)>f(2)
6.计算.
3 8 15 211[( ) ] ( 4) ( )
28
.
7.设
2 21
mn
mnx x a
,求
2
1xx .
8.已知
1
()
31x
f x m
是奇函数,则 ( 1)f = .
9.函数
1( ) 1( 0, 1)xf x a a a 的图象恒过定点 .
10 .若函数 0, 1xf x a b a a 的 图 象 不 经 过 第 二 象 限 , 则 ,ab满 足 的 条 件
是 .
11.先化简,再求值: (1)
23
2
a b a
b a b ,其中 256, 2006ab;
(2)
1 1 3
1 2 1 22 2 2[ ( ) ( ) ]a b a b a
,其中
1
3
8
12,
2
ab
.
12.(1)已知 x[-3,2],求 f(x)=
111
42xx
的最小值与最大值.
(2)已知函数
2 33() xxf x a 在[0,2]上有最大值 8,求正数 a 的值.
(3)已知函数
2 2 1( 0, 1)xxy a a a a 在区间[-1,1]上的最大值是 14,求 a 的值.
13.求下列函数的单调区间及值域:
(1)
( 1)2( ) ( )
3
xxfx
; (2)
12
4
x
xy
; (3)求函数
2 32( ) 2 xxfx 的递增区间.
14.已知
2( ) ( 1)
1
x xf x a a
x
(1)证明函数 f(x)在 ( 1, ) 上为增函数;(2)证明方程 0)( xf 没有负数解.
必修 1 第 2 章 函数概念与基本初等函数Ⅰ
§2.3 对数函数
重难点:理解并掌握对数的概念以及对数式和指数式的相互转化,能应用对数运算性质及换
底公式灵活地求值、化简;理解对数函数的定义、图象和性质,能利用对数函数单调性比较
同底对数大小,了解对数函数的特性以及函数的通性在解决有关问题中的灵活应用.
考纲要求:①理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数
或常用对数;了解对数在简化运算中的作用;
②理解对数函数的概念;理解对数函数的单调性,掌握函数图像通过的特殊点;
③知道对数函数是一类重要的函数模型;
④了解指数函数
xya 与对数函数 logay x 互为反函数 ,1a o a .
经典例题:已知 f(logax)=
2
2
( 1)
( 1)
ax
xa
,其中 a>0,且 a≠1.
(1)求 f(x); (2)求证:f(x)是奇函数; (3)求证:f(x)在 R 上为增函数.
当堂练习:
1.若 lg 2 ,lg3ab,则 lg 0.18 ( )
A. 22ab B. 22ab C.32ab D. 31ab
2.设 a 表示
1
35 的小数部分,则 2log (2 1)a a 的值是( )
A. 1 B. 2 C.0 D.
1
2
3.函数
2lg( 3 6 7)y x x 的值域是( )
A.[1 3,1 3] B.[0,1] C.[0, ) D.{0}
4.设函数
2
00
,0
( ) , ( ) 1,
lg( 1), 0
xx
f x f x x
xx
若 则
的取值范围为( )
A.(-1,1) B.(-1,+∞) C.( ,9) D.( , 1) (9, )
5.已知函数
1( ) ( )
2
xfx
,其反函数为 ()gx,则
2()gx 是( )
A.奇函数且在(0,+∞)上单调递减 B.偶函数且在(0,+∞)上单调递增
C.奇函数且在(-∞,0)上单调递减 D.偶函数且在(-∞,0)上单调递增
6.计算 2008 3 2log [log (log 8)] = .
7.若 2.5x=1000,0.25y=1000,求
11
xy
.
8.函数 f(x)的定义域为[0,1],则函数 3[log (3 )]fx 的定义域为 .
9.已知 y=loga(2-ax)在[0,1]上是 x 的减函数,则 a 的取值范围是 .
10.函数 ( )( )y f x x R图 象 恒 过 定 点 (0,1) ,若 ()y f x 存在反函数
1()y f x ,则
1( ) 1y f x的图象必过定点 .
11.若集合{x,xy,lgxy}={0,|x|,y},则 log8(x2+y2)的值为多少.
12.(1) 求函数 22(log )(log )
34
xxy
在区间[2 2,8] 上的最值.
(2)已知
2
11
22
2log 5log 3 0,xx
求函数
21
2
4( ) (log ) (log )
8
xfx
x
的值域.
13.已知函数
1( ) log ( 0, 1)
1a
mxf x a a
x
的图象关于原点对称. (1)求 m 的值;
(2)判断 f(x) 在 (1, ) 上的单调性,并根据定义证明.
14.已知函数 f(x)=x2-1(x≥1)的图象是 C1,函数 y=g(x)的图象 C2 与 C1 关于直线 y=x 对
称.
(1)求函数 y=g(x)的解析式及定义域 M;
(2)对于函数 y=h(x),如果存在一个正的常数 a,使得定义域 A 内的任意两个不等的值 x1,
x2 都有|h(x1)-h(x2)|≤a|x1-x2|成立,则称函数 y=h(x)为 A 的利普希茨Ⅰ类函数.试证明:
y=g(x)是 M 上的利普希茨Ⅰ类函数.
必修 1 第 2 章 函数概念与基本初等函数Ⅰ
§2.4 幂函数
重难点:掌握常见幂函数的概念、图象和性质,能利用幂函数的单调性比较两个幂值的大小.
考纲要求:①了解幂函数的概念;
②结合函数
1
23 21, , , ,y x y x y x y y x
x
的图像,了解他们的变化情况.
经典例题:比较下列各组数的大小:
(1)1.5 3
1
,1.7 3
1
,1; (2)(-
2
2 ) 3
2
,(-
10
7 ) 3
2
,1.1 3
4
;
(3)3.8 3
2
,3.9 5
2
,(-1.8) 5
3
; (4)31.4,51.5.
当堂练习:
1.函数 y=(x2-2x) 2
1-
的定义域是( )
A.{x|x≠0 或 x≠2} B.(-∞,0) (2,+∞) C.(-∞,0) [2,+∞ ) D.( 0,
2)
3.函数 y= 5
2
x 的单调递减区间为( )
y
x0
c1
c2
A.(-∞,1) B.(-∞,0) C.[ 0,+∞ ] D.(-∞,
+∞)
3.如图,曲线 c1, c2 分别是函数 y=xm 和 y=xn 在第一象限的图象,
那么一定有( )
A.nn>0 D.n>m>0
4.下列命题中正确的是( )
A.当 0 时,函数 yx 的图象是一条直线 B.幂函数的图象都经过(0,0),( 1,1)
两点
C.幂函数的 yx 图象不可能在第四象限内 D.若幂函数 yx 为奇函数,则在定义域
内是增函数
5.下列命题正确的是( )
幂函数中不存在既不是奇函数又不是偶函数的函数
图象不经过(—1,1)为点的幂函数一定不是偶函数
如果两个幂函数的图象具有三个公共点,那么这两个幂函数相同
如果一个幂函数有反函数,那么一定是奇函数
6.用“<”或”>”连结下列各式: 0.60.32 0.50.32 0.50.34, 0.40.8 0.40.6 .
7.函数 y=
22
1
mmx - - 在第二象限内单调递增,则 m 的最大负整数是_______ _.
8.幂函数的图象过点(2,
1
4 ), 则它的单调递增区间是 .
9 .设 x ∈ (0, 1) , 幂 函 数 y = ax 的 图 象 在 y = x 的 上 方 , 则 a 的 取 值 范 围
是 .
10.函数 y=
3
4x
在区间上 是减函数.
11.试比较
53
0.75380.16 ,1.5 , 6.25 的大小.
12.讨论函数 y=x 5
4
的定义域、值域、奇偶性、单调性。
13.一个幂函数 y=f (x)的图象过点(3,
4 27 ),另一个幂函数 y=g(x)的图象过点(-8, -2),
(1)求这两个幂函数的解析式; (2)判断这两个函数的奇偶性; (3)作出这两个函
y
x0
y
x0
y
x0
(1) (2) (3)
数的图象,观察得 f (x)< g(x)的解集.
14.已知函数 y=
4 2215 xx-- .
(1)求函数的定义域、值域; (2)判断函数的奇偶性; (3)求函数的单调区间.
必修 1 第 2 章 函数概念与基本初等函数Ⅰ
基本初等函数Ⅰ单元测试
1.碘 —131 经常被用于对甲状腺的研究,它的半衰期大约是 8 天(即经过 8 天的时间,有 一
半的碘—131 会衰变为其他元素).今年 3 月 1 日凌晨,在一容器中放入一定量的碘 —131,
到 3 月 25 日凌晨,测得该容器内还 剩有 2 毫克的碘—131,则 3 月 1 日凌晨,放人该容器
的碘—131 的含量是( )
A.8 毫克 B.16 毫克 C.32 毫克 D.64 毫克
2.函数 y=0.5x、 y=x-2 、y=log0.3x 的图象形状
如图所示,依次大致是 ( )
A.( 1)( 2)( 3) B.( 2)( 1)( 3)
C.( 3)( 1)( 2) D.( 3)( 2)( 1)
3.下列函数中,值域为(-∞,+∞)的是( )
A.y=2x B.y=x2 C.y=x-2 D.y=log ax (a>0, a
≠1)
4.下列函数中,定义域和值域都不是(-∞,+∞)的是( )
A.y=3x B.y=3x C.y=x-2 D.y=log 2x
5.若指数函数 y=ax 在[-1,1]上的最大值与最小值的差是 1,则底数 a 等于
A.
15
2
B.
15
2
C.
15
2
D.
5
2
1
6.当 0(1-a)b B.(1+a)a>(1+b)b C.(1-a)b>(1-a) 2
b
D.(1-a)a>(1-
b)b
7.已知函数 f(x)=
2log ( 0)
3 ( 0)x
xx
x
,则 f[f(
1
4 )]的值是( )
A.9 B.
1
9 C.-9 D.-
1
9
8.若 0<a<1,f(x)=|logax|,则下列各式中成立的是( )
A.f(2)>f(
1
3 )>f(
1
4 ) B.f( )>f(2)>f( ) C.f( )>f(2)>f( ) D.f( )>f( )>f(2)
9.在 f1(x)=
1
2x ,f2(x)=x2,f3(x)=2x,f4(x)=log
1
2 x 四个函数中,当 x1>x2>1 时,
使 2
1
[f(x1)+f(x2)] 0 的解集是( )
A. (-1,3) B.[-1,3] C.( , 1) (3, ) D. ( , 1] [3, )
2.已知 f(x)=1-(x-a)(x-b),并且 m,n 是方程 f(x)=0 的两根,则实数 a,b,m,n 的大小关系可能
是( )
A. m4 C.x<1 或 x>3 D.x<1
4. 设方程 2x+2x=10 的根为 ,则 ( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
5.如果把函数 y=f(x)在 x=a 及 x=b 之间的一段图象近似的看作直线的一段,设 a≤c≤b,那
么 f(c)的近似值可表示为( )
A.
1 [ ( ) ( )]
2
f a f b
B. ( ) ( )f a f b C.f(a)+
[ ( ) ( )]caf b f a
ba
D.f(a)-
[ ( ) ( )]caf b f a
ba
6.关于 x 的一元二次方程 x2+2(m+3)x+2m+14=0 有两个不同的实根,且一根大于 3,一根小于
1,则 m 的取值范围是 .
7. 当 a 时,关于 x 的一元二次方程 x2+4x+2a-12=0 两个根在区间[-3,0]中.
8.若关于 x 的方程 4x+a·2x+4=0 有实数解,则实数 a 的取值范围是___________.
9.设 x1,x2 分别是 log2x=4-x 和 2x+x=4 的实根,则 x1+x2= .
10.已知
32()f x x bx cx d ,在下列说法中:
(1)若 f(m)f(n)<0,且 m0,且 m0,且 m2; (2)求实数 a 的取值范围.
必修 1 必修 1 综合测试
1.设全集 U=R,集合 { }| 1 1A x x x或= < - ? , { }| ln 0B x x=?,则 ()U ABð 为( )
A.{ }| 1 0xx-? B.{ }| 0 1xx-2
时, g(t)=f(t).
(2) ①当 -2-t (t+1)-(-2), 即 t
5
2
时, h(t)= f(t); ②当-2-t< (t+1)-(-2), 即 t
5
2
时, h(t)=
f(t+1).
综上所述:
2
2
6 8( 3)
( ) 1( 3 2)
4 3( 2)
t t t
g t t
t t t
,
2
2
54 3( )
2()
56 8( )
2
t t t
ht
t t t
14. 解:(1)当 02x时,S=x;当 24x时,S=2;当 46x时,S=6-x。 定义域是
(0,6),值域是(0,2) (2) f[f(3)]=f(2)=2.
§2.1.2 函数的简单性质
经典例题:
解析:本题可采用三种解法.
方法一:直接根据奇、偶函数的定义.
由 f(x)是奇函数得 f(-a)=-f(a), f(-b)=-f(b), g(a)=f(a), g(b)=f(b),
g(-a)=g(a), g(-b)=g(b).
∴以上四个不等式分别可简化为①f(b)>0;②f(b)<0;③f(a)>0;④f(a)<0.
又∵f(x)是奇函数又是增函数,且 a>b>0,故 f(a)>f(b)>f(0)=0,从而以上不
等式中①、③成立.故选 C.
方法二:结合函数图象.
由下图,分析得 f(a)=g(a)=g(-a)=-f(-a), f(b)=g(b)=g(-b)=-f(-b).
从而根据所给结论,得到①与③是正确的.故选 C.
方法三:利用间接法,即构造满足题意的两个函数模型 f(x)=x,g(x)=|x|,取特殊值 a、
b.如 a=2,b=1.可验证正确的是①与③,故选 C.
答案:C
当堂练习:
B ; 2. D ; 3. B ;4. D ;5. A ; 6.
2
( 0)
( ) 2 (0 1)
5 2( 1)
tt
g t t t t
tt
;7.
2 3( 1) ( )
4
f x x f
;
8. 1()fx > 2()fx ;9. x=-1; 10. ( 3,1 );
11. 解: (1)函数
1( ) 2
2
f x x
x
,设 121 xx时, 12( ) ( )f x f x
12
12
11( ) ( )
22
xx
xx
12
12
1( )(1 ) 0
2
xx
xx
,所以 ()fx在区间[1, ) 上单调递增;
(2)从而当 x=1 时, )(xf 有最小值
7
2 .
12. 解:(1)任取 1x , ],[2 nmx ,且 12xx ,
12
122
12
1( ) ( ) xxf x f x
a x x
, 因为 12xx ,
1x , ,所以 12 0xx ,即 12( ) ( )f x f x ,故 )(xf 在 ],[ nm 上单调递增.
(2)因为 在 上单调递增, )(xf 的定义域、值域都是 ],[ nm ( ) , ( )f m m f n n,
即 nm, 是方程 2
21 1a
a ax x 的两个不等的正根 01)2( 222 xaaxa 有两个不等的正根.
所以 04)2( 222 aaa ,
2
2
2 0aa
a
1
2a
∴ ),(,)(3344 2
1
3
162
3
2121 aaamn aa ,
∴ 2
3a 时, mn 取最大值 3
34
.
13.解: (1)利用定义易证之; (2)由(1)得 ( ) ( ) ( )f x F x G x=
23(2 3) (3 )x x x .
14. 解: (1)
22( ) 4( 2) 1f x x ; (2)当 ( ,0]x 时, f1(x)单调递减, 当 [0, )x 时, f1(x)
单调递增; 当 ( ,1]z 时, f2(z) 单调递减, 当 [1, )z 时, f1(x)单调递增.
(3) 当 ( , 2]x 和 [0, 2]x 时, f(x)分别单调递减;
当 [ 2, )x 和 [ 2, 0]x 分别单调递增.
§2.1.3 单元测试
1.C; 2. A; 3.C; 4.C; 5.B; 6.C; 7.B; 8.D; 9.B; 10.D; 11.D; 12.B;
13. 2.5; 14. g(x)=2x-3; 15. 1 或 2; 16. x6-6x4+9x2-2;
17.解: (1)在 ( , 1] 和[1,3] 上分别单调递减; 在[-1,1]和[3, ) 上分别单调递增.
(2) 值域是[0,4]
18.(1)证明:对任意 x1、x2∈R,∵a>0,∴f(x1)+f(x2)-2f(
12
2
xx
)
=ax12+x1+ax22+x2-2[a(
12
2
xx
)2+
12
2
xx
]
=
1
2 a(x1-x2)2≥0.∴f(
12
2
xx
)≤ [f(x1)+f(x2)], ∴f(x)是凹函数.
19.(1)证明:令 x=y=0,则 f(0)+f(0)=f(0),故 f(0)=0.
令 y=-x,则 f(x)+f(-x)=f( 21
xx
x
)=f(0)=0.∴f(-x)=-f(x),即函数 f(x)是奇函数.
(2)证明:设 x1<x2∈(-1,1),则 f(x1)-f(x2)=f(x1)+f(-x2)=f(
12
121
xx
xx
).
∵x1<x2∈(-1,1),∴x2-x1>0,-1<x1x2<1.因此
12
121
xx
xx
<0,∴f(
12
121
xx
xx
)>0,
即 f(x1)>f(x2).∴函数 f(x)在(-1,1)上是减函数.
20.解:(1)设 P(x1,y1),Q(x2,y2)(x1≠x2)是函数 f(x)=
31x
xa
的图象上的两个“稳定点”,
∴
1
1
1
2
2
2
31
31
x
x
xa
x
x
xa
,即有 x12+ax1=3x1-1(x1≠-a),x22+ax2=3x2-1(x2≠-a).
有 x12+(a-3)x1+1=0(x1≠-a),x22+(a-3)x2+1=0(x2≠-a).
∴x1、x2 是方程 x2+(a-3)x+1=0 两根,且 ∵x1, x2≠-a,∴x≠-a,
∴方程 x2+(a-3)x+1=0 有两个相异的实根且不等于-a.
∴
2
2
( 3) 4 1 0,
( ) ( 3)( ) 1 0.
a
a a a
∴a>5 或 a<1 且 at≠-
1
3 .
∴a 的范围是(-∞,- )∪(- ,1)∪(5, ∵f(x)是 R 上的奇函数,
∴f(-0)=-f(0),即 f(0)=0.∴原点(0,0)是函数 f(x)的“稳定点”,若 f(x)还有稳定点(x0,y0),
则∵f(x)为奇函数,f(-x0)=-f(x0),f(x0)=x0,∴f(-x0)=-x0,这说明:(-x0,-x0)也是
f(x)的“稳定点”.综上所述可知,f(x)图象上的“稳定点”除原点外是成对出现的,而且原点
也是其“稳定点”,
∴它的个数为奇数.
§2.2 指数函数
经典例题:
解:由题意可知,函数 y=3 322 xx 的定义域为实数 R.设 u=-x2+2x+3(x∈R),则 f(u)
=3u,
故原函数由 u=-x2+2x+3 与 f(u)=3u 复合而成.∵f(u)=3u 在 R 上是增函数,而 u=-
x2+2x+3
=-(x-1)2+4 在 x∈(-∞,1)上是增函数,在[1,+∞]上是减函数.
∴y=f(x)在 x∈(-∞,1)上是增函数,在[1,+∞]上是减函数.
又知 u≤4,此时 x=1,∴当 x=1 时,yam=f(1)=81,而 3 >0,
∴函数 y=f(x)的值域为(0,81)
当堂练习:
1.A ; 2. C ; 3. B ;4. A ;5. A ; 6. 1 ;7. 2
nm
mna
;8.
1
4 ;9. (1,0);10. 1, 1ab;
11.(1) 原式=
1
1 1 1 1 12 3 2 3 2
872 2 2 2 2
2{ [ ( ) ] } { [ ] } 128a b a a b a a
b a b b a b
(2)原式= 1 2 2 3 3 4a b ab a a b
4
8
122 ( )
42
12. (1) 解:f(x)=
21 1 1 31 4 2 1 2 1 (2 )
4 2 2 4
x x x x
xx
, ∵ x [-3,2], ∴
1 28
4
x
.则当 2-x= 2
1
,即 x=1 时,f(x)有最小值 4
3
;当 2-x=8,即 x=-3 时,f(x)有最大值 57.
(2)解:设
2233( ) 3 3 ( )
24
g x x x x
,当 x [0,2]时,
max min
3( ) 3, ( )
4
g x g x
,
当 01 时,
3 8, 2aa.综上所述,a=2.
(3)原函数化为
2( 1) 2xya ,当a>1时,因 [ 1,1]x ,得
1[ , ]xa a a ,从而
2( 1) 2 14, 3aa ,
同理, 当 01 时,f(x) 在 (1, ) 上单调递减;
当 01 从而 -lga>lgc,得 lg(ac)<0, 01ac .
19.(1)它是偶函数; (2) 函数 f (x)在 x∈[0, +∞]上是单调递增函数;
(3) 2y=ex+e-x, ∴e2x-2yex+1=0, 解得 ex=y+
2 1y , ∴
12( ) ln( 1)f x x x ,
x≥1.
20.(1)由 0xxab,∴
( ) 1xa
b
,
1a
b
.∴ x>0, ∴ 定义域为(0,+∞).
(2)设 210xx,a>1>b>0,∴ 21xxaa 12xxbb 21xxbb
∴ 2 2 1 1 0x x x xa a a b ∴
22
11
1
xx
xx
ab
ab
.∴ 21( ) ( ) 0f x f x.
∴ ()fx在(0,+∞)是增函数.
(3)当 (1x ,+∞) 时, ( ) (1)f x f ,要使 ( ) 0fx ,须 (1) 0f , ∴ a-b≥1.
§2.5 函数与方程
经典例题:解:设 y=|x2-2x-3|和 y=a,利用 Excel、图形计算器或其他画图软件,分别作
出这两个函数的图象,它们的交点的个数,即为所给方程实根的个数.如下图,当 a=0 或 a
>4 时,有两个实根;当 a=4 时,有三个实根;当 0<a<4 时,有四个实根.
当堂练习:
1.C ; 2. A ; 3. C ;4. C ;5. C ; 6.
21
4
m
; 7.
15 8
2
a
; 8.a≤-4; 9. 4; 10. (2);
11.设 f(x)= mx2+2(m+3)x+2m+14,根据图象知当
0
(4) 0
m
f
或
0
(4) 0
m
f
时,符合题意
从而得
19 0
13
m
.
12. (1)设抛物线与 x 轴相交于点(x1,0),(x2,0),则
12
21,
( 1)
axx
aa
12
1
( 1)
xx
aa
,
得
2
2 1 2 1 1 2
1( ) 4
( 1)
l x x x x x x
aa
;
(2)
1 2 3
1 1 1
1 2 2 3 ( 1)nl l l l
nn
=
1 1 1 1 1 1( ) ( ) ( )
1 2 2 3 1nn
= 1
n
n
13.(1)由
22( ) ( ) 2 0, (1) 0g x bx f x ax bx c ax bx c f a b c 与 得 ,
2, 0, 0, 4 0,a b c a c b ac 从而 即函数 ( ) ( )f x g x与 的图象交于不同两点 A,B;
(2)
, , , 2 , 2,bc a b a b c a c a b a b
a
即 得
知函数 F(x)在[2,3]上为增函
数, (2) 3 3 9, (3) 8 5 21, 2, 1;F a b F a b a b 解得
(3)设方程
12
2
12
12
2
( ) 2 0 , ,
bxx
aF x ax bx c x x
cxx
a
的两根为 得
2 2 2
1 1 1 2 1 2
13| | ( ) 4 4[( ) ],
24
cA B x x x x
a
1, , , ( 2, ),
2
ca b c b a c a a c c
a
由 得
设
22
11
13| | ( ) 4[( ) ],
24
ccA B h
aa
的 对 称 轴 为
11, ( ) ( 2, )
22
ccxh
aa
在
上 是 减 函 数
2
1 1 1 1| | (3,12), | | ( 3, 2 3).A B A B 得
14.解:原方程转化为
10
30
0
( 1)(3 )
x
x
ax
x x a x
,即方程 x2-5x+a+3=0 在区间(1,3)内是否有根,由
0 得:
13
4
a
,设 f(x)= x2-5x+a+3,对称轴是
5
2
x
,若
(1) 1 0
(3) 3 0
fa
fa
得有一根在区间(1,3)
内,即当 13(1,3)
4
a
时,原方程有一根; 若
(1) 1 0
(3) 3 0
0
fa
fa
得
13(3, )
4
a
时,原方程有两根;
13(1, ]
4
a
时, 原方程无解.
§2.6 函数模型及其应用
经典例题:解:设 x 年后我国人口总数为 y,则有 y=12·( 1+0.0125)x,依题意,得 y>14,
即 12·( 1+0.0125)x>14,即(1+0.0125)x>
14
12 .
两边取对数,得 xlg1.0125>lg14-lg12.所以 x>
lg14 lg12
lg1.125
≈12.4.
答:13 年后,即 2008 年我国人口总数将超过 14 亿.
当堂练习:
1.A ; 2. C ; 3. D ;4. A ;5. C ; 6. 神州行; 7. y= -10x+560,31, 6250; 8. 2500; 9. 大于 34; 10.
600
2cm ;
11. (1)依题得,
6 0 1
2 20 1 10
33
tt
y
tt
(2)设第二次服药时在第一次服药后 t1 小时,则 44 13
2013
2 tt ,因而第二次服药应在
11:00; 设第三次服药在第一次服药后 t2 小时,则此时血液中含药量应为两次服药量的和,
即有 ,4)4( 3
2023
2
3
2023
2 tt 解得 t2=9 小时,故第三次服药应在 16:00;设第四次服药在第
一次后 t3 小时(t3>10),则此时第一次服进的药已吸收完,此时血液中含药量应为第二、
三次的和, ,4)9()4( 3
2023
2
3
2023
2 tt 解得 t3=13.5 小时,故第四次服药应在 20:30.
12.设每日来回 y 次,每次挂 x 节车厢,由题意,y=kx+b,且当 x=4 时,y=16;当 x=7 时,y=10.
解得:k=-2,b=24,∴y=-2x+24. 由题意,每次挂车厢最多时,营运人数最多,设每日拖
挂 W 节车厢,则 W=2xy=2x(-2x+24)=-4x2+48x=-4(x-6)2+144,
∴当 x=6 时,Wmax=144,此时,y=12,最多营运 15840 人.
13.解:依题意,价格上涨 x%后,销售总金额为: y=a(1+x%)· b(1-kx%)= 10000
ab
[-kx2+100(1
-k)x+10000]. (1)取 k=
1
2 ,y= [- x2+50x+10000],∴x = 50, 即商品价格上
涨 50%时, y 最大为
9
8 ab. (2)因为 y= [-kx2+100(1-k)x+10000],此二次函数
开口向下,对称轴为 x=
50(1 )k
k
,在适当涨价过程中,销售总金额不断增加,即要求此函
数当自变量 x 在{x|x>0}的一个子集中增大时,y 也增大.所以 >0,解之 0<k<1.
14.设二次函数为 y=px2+qx+r,则
1 0.05
4 2 1.2 0.35
9 3 1.3 0.7
p q r p
p q r q
p q r r
,
所以
20.05 0.35 0.7y x x ,当 x=4 时, y=1.3;
对于函数
xy ab c,由
2
3
1 0.8
1.2 0.5
1.41.3
ab c a
ab c b
cab c
,所以
10.8 ( ) 1.4
2
xy
,当 x=4 时, y=1.35,
显然,用函数
10.8 ( ) 1.4
2
xy
作为模拟函数较好.
函数的概念与基本初等函数Ⅰ章节测试
1.D; 2.D; 3.C; 4.C; 5.D; 6.C; 7.A; 8.D; 9.B; 10.D; 11.
5[2, ]
2 ; 12.3; 13. 0,2 或-
1 17
4
;
14. FB; 15.(-∞,-1)∪(1,+∞);
16. 2
2
11( ) log ( ) log ( )
a a
f x a x ax 11( log 2)( log )
22aaxx 21 3 1(log )
2 2 8a x
,因 x[2,4],
函数的最小值为
1
8
,所以 0
,
1(0) 1 2 2( ) 0
2
f t t= - = - <
,
1 1 1 3( ) (2 1) 1 2 0
2 4 2 4
f t t t= + - + - = - >
,
所以方程 ( ) 0fx= 在区间
( )1,0 )
1及(0,
2
-
上各有一个实数根.
18. (1)函数 ()fx为 R 上的增函数.证明如下:
函数 的定义域为 R,对任意
12,xx RÎ , 1 2 2 1
1 2 1 2
2 2 2 2( ) ( ) ( ) ( )
2 1 2 1 2 1 2 1x x x x
x x f x f x a a,且 有< - = - - - = -
+ + + +
12
21
2(2 2 )
(2 1)(2 1)
xx
xx
-=
++.
因为 2xy = 是 R 上的增函数, 12xx< ,所以 1222xx- <0,
所以 12( ) ( )f x f x- <0即 12( ) ( )f x f x< ,函数 ()fx为 R 上的增函数.
(2)存在实数 a=1,使函数 ()fx为奇函数.
证明如下:当 a=1 时,
2( ) 1
21x
fx=-
+ =
21
21
x
x
-
+ .
对任意 x RÎ , ()fx-=
21
21
x
x
-
-
-
+ =
12
12
x
x
-
+ =-
21
21
x
x
-
+ =- ()fx,即 ()fx为奇函数.
19. (1)过点 B 作 BD^ AX,D 为垂足,由于 AC=x,AB=50,BD=30 所以 AD=40,CD
=40-x,
由勾股定理得 2 2 2 2 2(40 ) 30BC CD BD x= + = - + .根据题意得:
22
12((40 ) 30 )y k x k x= + - + ,
即
2
2 2 1 2(80 ) 2500y k x k k x k= - - + ( 0x > ).
(2)因为 1220kk= ,所以 y
2
2 2 260 2500k x k x k= - + ,当
2
2
60
30
2
k
x
k
-
= - =
时, min 21600yk .
答:当 x =30km 时,单位重量货物的总运费最小,最小值为 1600 2k 元.
20. (1)∵
1( ) 1fx
ax
,∴
11( ) ( ) ( 1 ) ( 1 ) 2f a x f a x
xx
,由已知定理
得, ()y f x 的图象关于点 ( , 1)a 成中心对称;
(2)首先证明 ()fx在[ 2, 1]aa上是增函数,为此只要证明 在 ( , )a 上是增函数.
设 12x x a ,则
12
12
1 2 1 2
11( ) ( ) 0
( )( )
xxf x f x
a x a x a x a x
,
∴ 在 ( , )a 上是增函数.
再由 在[ 2, 1]aa上是增函数得,
当 [ 2, 1]x a a 时, ( ) [ ( 2), ( 1)]f x f a f a ,即
1( ) [ , 0]
2
fx
;
(3)∵构造过程可以无限进行下去,∴
1() xaf x a
ax
对任意 xA 恒成立,
∴方程
1xaa
ax
无解,即方程
2( 1) 1a x a a 无解或有唯一解 xa ,
∴
2
10
10
a
aa
或
2
10
1
1
a
aa a
a
,由此得到 1a .
w.w.w.g.k.x.x.c.o.m