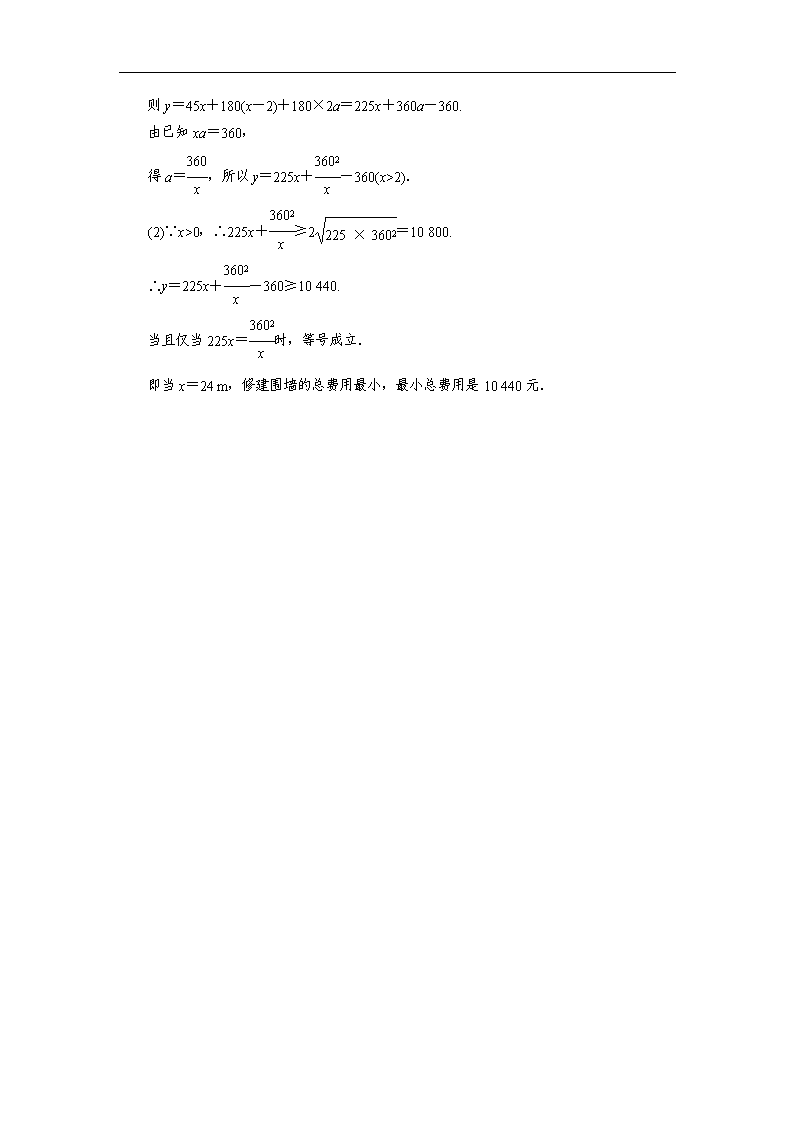高考数学复习练习试题7_4基本不等式:≤ (a>0,b>0)
§7.4 基本不等式:≤ (a>0,b>0)
一、填空题(本大题共9小题,每小题6分,共54分)
1.下列结论中不正确的是________.(填序号)
①a>0时,a+≥2 ②+≥2
③a2+b2≥2ab ④a2+b2≥
2.已知0
0,直线(b2+1)x+ay+2=0与直线x-b2y-1=0互相垂直,则ab的最小值等于__________.
5.已知x>0,y>0,且+=1,若x+2y>m2+2m恒成立,则实数m的取值范围是________________________________________________________________________.
6.(2010·山东)已知x,y∈R+,且满足+=1,则xy的最大值为________.
7.(2010·镇江月考)若x>1,则x+的最小值为________.
8.(2010·无锡模拟)已知圆C:x2+y2+bx+ay-3=0 (a,b为正实数)上任意一点关于直线l:x+y+2=0的对称点都在圆C上,则+的最小值为________.
9.(2010·安徽)若a>0,b>0,a+b=2,则下列不等式对一切满足条件的a,b恒成立的是________(写出所有正确命题的编号).
①ab≤1;②+≤;③a2+b2≥2;
④a3+b3≥3;⑤+≥2.
二、解答题(本大题共3小题,共46分)
10.(14分)求y= (x>0)的最小值.
11.(16分)已知a,b>0,求证:+≥.
12.(16分)(2009·湖北)围建一个面积为360 m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2 m的进出口,如图所示.已知旧墙的维修费用为45 元/m,新墙的造价为180元/m,设利用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
答案
1.② 2. 3.50 4.2 5.-40,
a+b≥2>0,
∴(a+b)≥2·2=4.
∴+≥.当且仅当取等号.
即a=b时,不等式等号成立.
12.解 (1)如图,设矩形的另一边长为a m,
则y=45x+180(x-2)+180×2a=225x+360a-360.
由已知xa=360,
得a=,所以y=225x+-360(x>2).
(2)∵x>0,∴225x+≥2=10 800.
∴y=225x+-360≥10 440.
当且仅当225x=时,等号成立.
即当x=24 m,修建围墙的总费用最小,最小总费用是10 440元.