- 2021-06-15 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学人教B版必修4教案:1-3-2 余弦函数、正切函数的图象与性质含答案
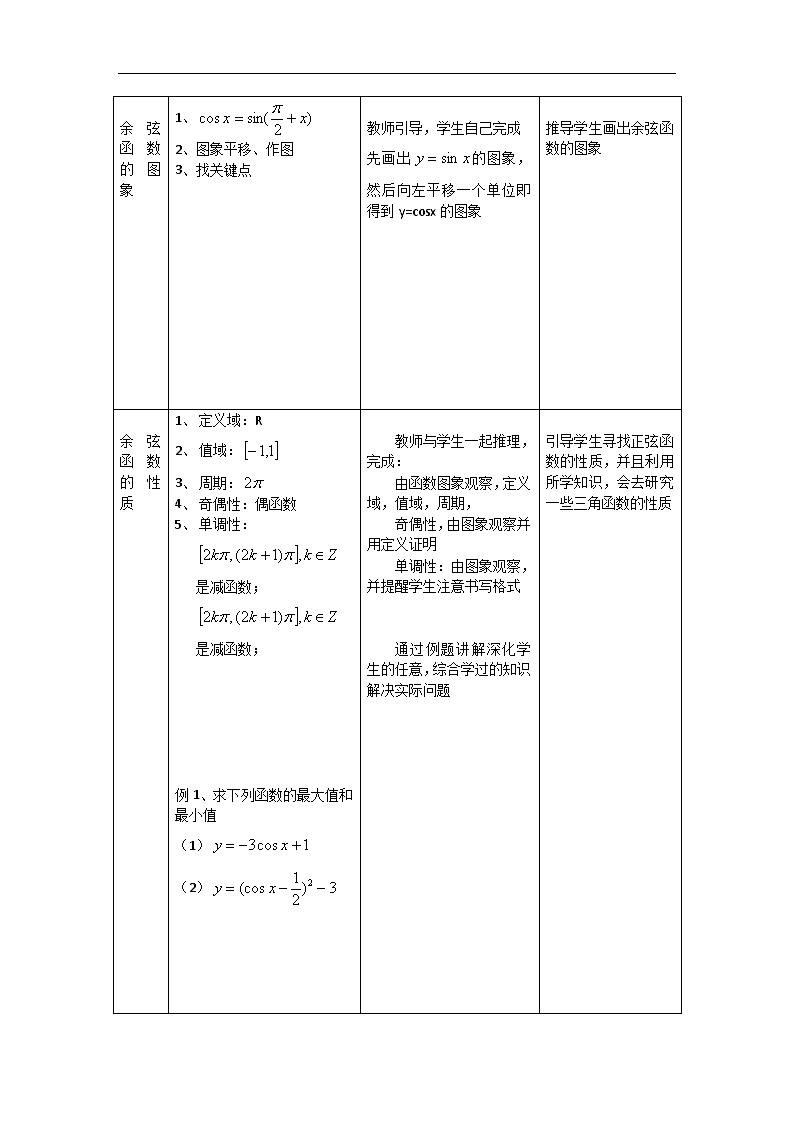
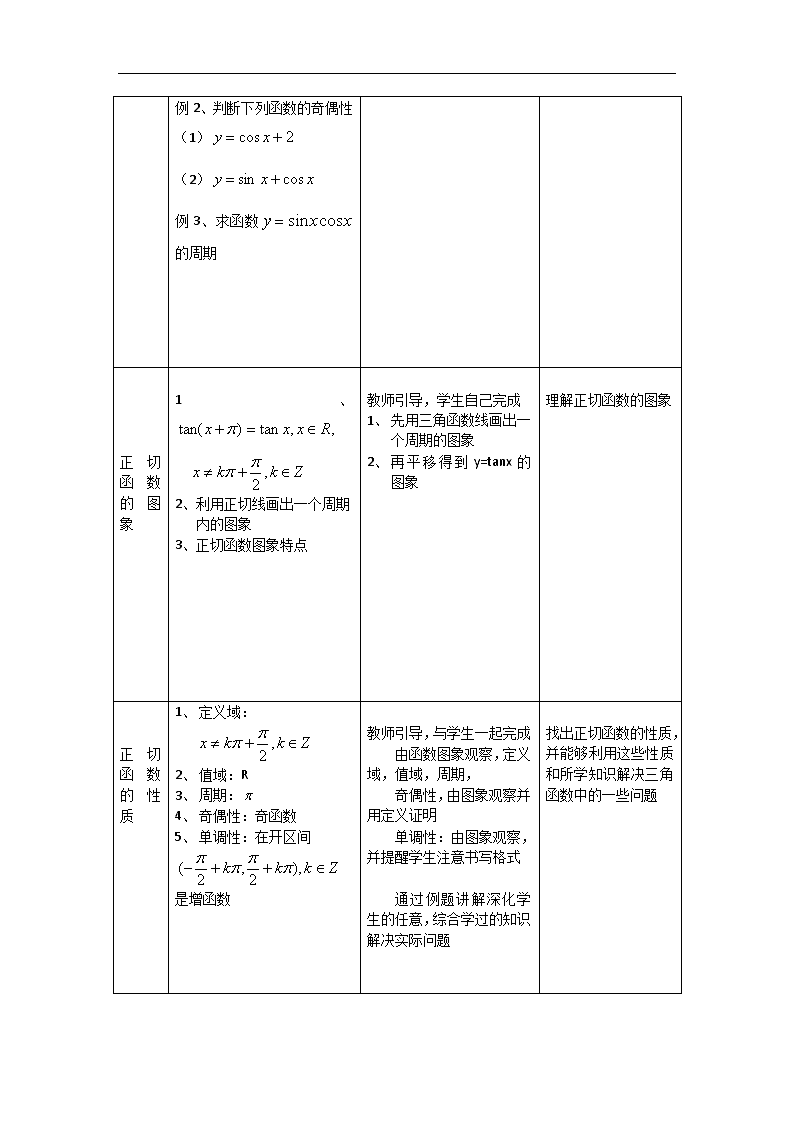
1.3.2 余弦函数、正切函数的图象与性质 一、教学目标 1、知识目标 (1)理解余弦函数的图象与性质 (2)理解正切函数的图象与性质 2、能力目标 (1)引导学生自己由所学的知识推导未知的知识,根据正弦函数的图象、诱导 公式推导出余弦函数的图象,并自己总结其性质 (2)引导学生仿照对正弦函数的研究,自己利用三角函数线得出正切函数的图 象,并研究它的性质 (3)培养学生利用所学知识解决问题的能力,以及发现问题,研究问题的能力 3、情感目标 (1)渗透数形结合的思想 (2)培养学生触类旁通的推理能力 (3)培养学生实践出真知的辨证唯物思想 二、教学重点、难点 本节重点是理解余弦函数和正切函数的图象和性质,难点余弦函数和正切函 数的图象和性质。 三、教学方法 引导学生进行推理,鼓励学生自主学习 四、教学过程 教学 环节 教学内容 师生互动 设计意图 复 习 引 入 复习 xy sin 的图象和性质 和图象变换的有关知识 教师提出问题,学生回答 诱导公式、 xy sin 的图 象和性质,函数图象的变换 等问题 为学生推导 xy cos 的 图 象 做 准备 余 弦 函 数 的 图 象 1、 )2sin(cos xx 2、图象平移、作图 3、找关键点 教师引导,学生自己完成 先画出 xy sin 的图象, 然后向左平移一个单位即 得到 y=cosx 的图象 推导学生画出余弦函 数的图象 余 弦 函 数 的 性 质 1、 定义域:R 2、 值域: 1,1 3、 周期: 2 4、 奇偶性:偶函数 5、 单调性: Zkkk ,)12(,2 是减函数; Zkkk ,)12(,2 是减函数; 例 1、求下列函数的最大值和 最小值 (1) 1cos3 xy (2) 3)2 1(cos 2 xy 教师与学生一起推理, 完成: 由函数图象观察,定义 域,值域,周期, 奇偶性,由图象观察并 用定义证明 单调性:由图象观察, 并提醒学生注意书写格式 通过例题讲解深化学 生的任意,综合学过的知识 解决实际问题 引导学生寻找正弦函 数的性质,并且利用 所学知识,会去研究 一些三角函数的性质 例 2、判断下列函数的奇偶性 (1) 2cos xy (2) xxy cossin 例 3、求函数 xxy cossin 的周期 正 切 函 数 的 图 象 1、 ,,tan)tan( Rxxx Zkkx ,2 2、利用正切线画出一个周期 内的图象 3、正切函数图象特点 教师引导,学生自己完成 1、 先用三角函数线画出一 个周期的图象 2、 再平移得到 y=tanx 的图 象 理解正切函数的图象 正 切 函 数 的 性 质 1、 定义域: Zkkx ,2 2、 值域:R 3、 周期: 4、 奇偶性:奇函数 5、 单调性:在开区间 Zkkk ),2,2( 是增函数 教师引导,与学生一起完成 由函数图象观察,定义 域,值域,周期, 奇偶性,由图象观察并 用定义证明 单调性:由图象观察, 并提醒学生注意书写格式 通过例题讲解深化学 生的任意,综合学过的知识 解决实际问题 找 出 正 切 函 数 的 性 质,并能够利用这些 性质和所学知识解决 三角函数中的一些问 题 例 4、求函数 )3tan( xy 的定义域 例 5、求函数 xy 3tan 的周 期 归纳 小结 从知识方法两方面对本节知 识进行总结 让学生来总结知识,进行反 思,找出收获, 教师归纳 关 注 学 生 的 自 主 体 验,反思和发表本堂 课的体验和收获 布置 作业 层次一:教材 57 页,练习 A 3,4,5 层次二:57 页教材,练习 B 3,4,5 作业分两个层次,第一层次 要所有学生完成,第二层次 要学有余力的学生完成 通过分层教学使学生 更好的完成本课学习查看更多