数学理卷·2018届广东省普宁市第二中学高二上学期期末考试（2017-01）

数学理卷·2018届广东省普宁市第二中学高二上学期期末考试（2017-01）

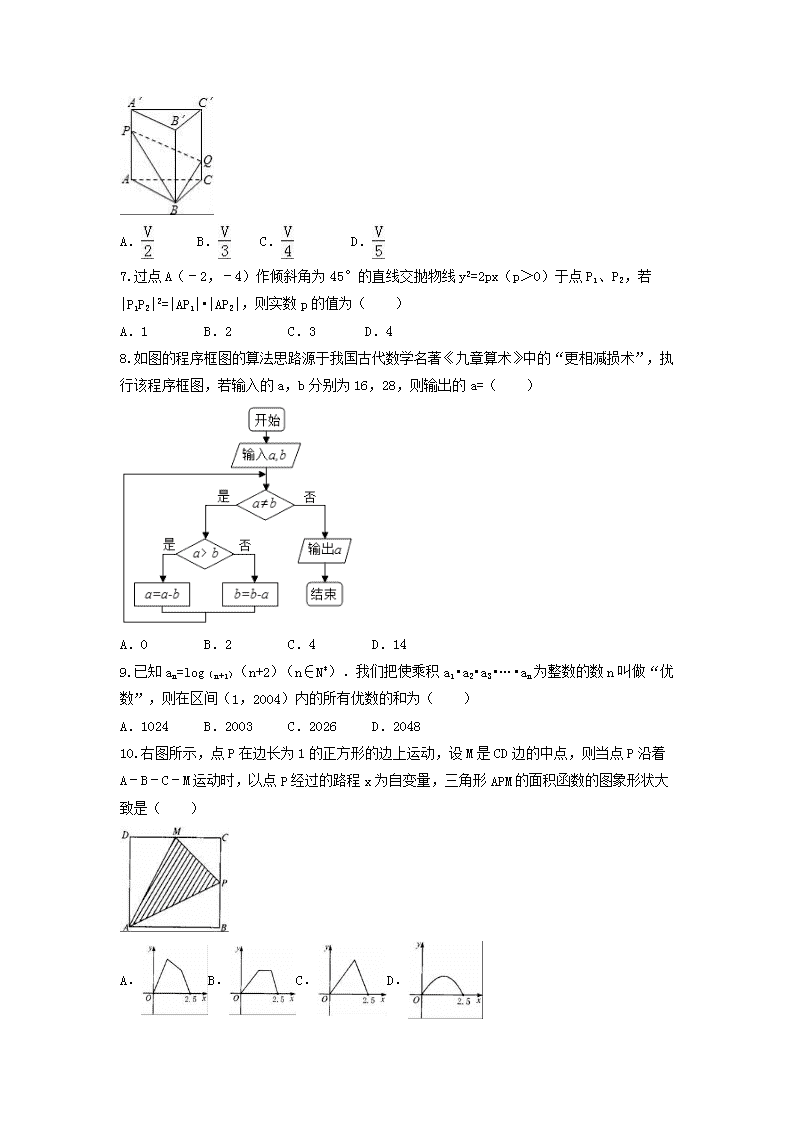
‎ 普宁市第二中学2018届高二级上学期·期末考试 ‎ 理科数学试题 ‎ 注意事项：‎ ‎1.答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卷上。‎ ‎2.用2B铅笔将选择题答案在答题卷对应位置涂黑；答案不能答在试卷上。‎ ‎3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内的相应位置上；不准使用铅笔或涂改液。不按以上要求作答的答案无效。‎ ‎4.考生必须保持答题卷的整洁。‎ 第I卷 选择题（每题5分，共60分）‎ 本卷共12题，每题5分，共60分，在每题后面所给的四个选项中，只有一个是正确的。‎ ‎1.已知集合A⊆{0，1，2}，且集合A中至少含有一个偶数，则这样的集合A的个数为（　　）‎ A．6 B．5 C．4 D．3‎ ‎2.已知复数的实部为﹣1，则复数z﹣b在复平面上对应的点在（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎3.已知△ABC的三内角A、B、C的对边边长分别为a、b、c．若a=b，A=2B，则cos B=（　　）‎ A． B． C． D．‎ ‎4.甲、乙、丙、丁、戊五位同学站成一排照相留念，则在甲乙相邻的条件下，甲丙也相邻的概率为（　　）‎ A．1 B． C． D．‎ ‎5.当 ，时，的最小值为（ ）‎ A．10 B．12 C．14 D．16‎ ‎6.如图直三棱柱ABC﹣A1B1C1的体积为V，点P、Q分别在侧棱AA1和CC1上，AP=C1Q，则四棱锥B﹣APQC的体积为（　　）‎ A． B． C． D．‎ ‎7.过点A（﹣2，﹣4）作倾斜角为45°的直线交抛物线y2=2px（p＞0）于点P1、P2，若|P1P2|2=|AP1|•|AP2|，则实数p的值为（　　）‎ A．1 B．2 C．3 D．4‎ ‎8.如图的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的a，b分别为16，28，则输出的a=（　　）‎ A．0 B．2 C．4 D．14‎ ‎9.已知an=log（n+1）（n+2）（n∈N*）．我们把使乘积a1•a2•a3•…•an为整数的数n叫做“优数”，则在区间（1，2004）内的所有优数的和为（　　）‎ A．1024 B．2003 C．2026 D．2048‎ ‎10.右图所示，点P在边长为1的正方形的边上运动，设M是CD边的中点，则当点P沿着A﹣B﹣C﹣M运动时，以点P经过的路程x为自变量，三角形APM的面积函数的图象形状大致是（　　） ‎ ‎ ‎ A．B．C．D．‎ ‎11.设两条直线的方程分别为x+y+a=0，x+y+b=0，已知a，b是方程x2+x+c=0的两个实根，且0≤c≤，则这两条直线之间的距离的最大值和最小值分别是（　　）‎ A．，B．， C．， D．，‎ ‎12.如果定义在上的函数满足：对于任意，都有，则称为“函数”．给出下列函数：‎ ‎①；②；③；④，其中“函数”的个数有（ ）‎ A．3个 B．2个 C．1个 D．0个 第Ⅱ卷（非选择题）‎ 二、填空题：（本大题共4小题，每小题5分，共20分）‎ ‎13.已知的展开式中的系数为1，则实数 .‎ ‎14. .‎ ‎15.已知，则 ‎ ‎16.已知，若在区间上有极值点，则的取值范围是 三、解答题：（本大题共6小题，满分70分.解答应写出文字说明、证明过程或演算步骤）‎ ‎17.（本小题满分12分）‎ 在中，AD是角A的平分线.‎ ‎(1)用正弦定理或余弦定理证明：；‎ ‎(2)已知AB=2.BC=4, ,求AD的长.‎ ‎18.（本小题满分12分）‎ ‎ 某市对所有高校学生进行普通话水平测试，发现成绩服从正态分布，下表用茎叶图列举出来抽样出的10名学生的成绩.‎ ‎(1)计算这10名学生的成绩的均值和方差；‎ ‎(2)) 给出正态分布的数据：‎ 由（1）估计从全市随机抽取一名学生的成绩在的概率.‎ ‎19.（本小题满分12分）‎ 等腰三角形ABC，E为底边BC的中点，沿AE折叠，如图，将C折到点P的位置，使P-AE-C为，设点P在面ABE上的射影为H.‎ ‎(1)证明：点H为EB的中点；‎ ‎(2)) 若，求直线BE与平面ABP所成角的正弦值.‎ ‎20.（本小题满分12分）‎ 已知直线是椭圆的右准线，若椭圆的离心率为，右准线方程为 ‎(1)求椭圆的方程；‎ ‎(2))已知一直线AB过右焦点，交椭圆于A,B两点，P为椭圆的左顶点，PA,PB与右准线交于点，问是否为定值，若是，求出该定值，否则说明理由.‎ ‎21.（本小题满分12分）‎ ‎ (1) 已知为常数，且，函数，求函数在上的最大值；‎ ‎(2)) 若为正实数，求证：‎ 请考生从第（22），（23）两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22.（本小题满分10分）选修4-4：参数方程与坐标系 以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，已知曲线的参数方程为，（为参数，且），曲线的极坐标方程为 ‎(1)求的极坐标方程与的直角坐标方程；‎ ‎(2))若P是上任意一点，过点P的直线交于点M,N，求的取值范围.‎ ‎23.（本题满分10分），选修4-5：不等式选讲 已知函数 ‎（1）解不等式；‎ ‎（2）若对任意，都有，使得成立，求实数的取值范围.‎ 普宁市第二中学2018届高二级上学期·期末考试 理科数学试题参考答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A B B B D B A C C A A A ‎13. 2‎ ‎14. ‎ ‎15. 2‎ ‎16‎ ‎17．解：（Ⅰ）证明：在中，由正弦定理得：‎ ‎.………………………………………………………………2分 在中，由正弦定理得：‎ ‎.………………………………………………………………4分 ‎∵，∴.‎ 又，∴.‎ ‎∴.………………………………………………………………6分 ‎（Ⅱ）在中，由余弦定理得：‎ ‎.‎ ‎∴.………………………………………………………………8分 由（Ⅰ）知，，‎ 又,‎ ‎∴.………………………………………………………………10分 在中，由余弦定理得：‎ ‎.‎ ‎∴.………………………………………………………………12分 ‎18．解：（Ⅰ）.…………3分 ‎.………………………………………………………………6分 ‎（Ⅱ）由（Ⅰ）可估计，，.‎ ‎∵‎ ‎，………………………………………………………………8分 ‎∴‎ ‎.………………………………………………………………12分 ‎19．解：（Ⅰ）依题意，，则，，.‎ ‎∴面.‎ 故为二面角的平面角，则点在面上的射影在上.‎ 由得.………………………………………………………………3分 ‎∴.‎ ‎∴为的中点. ………………………………………………………………6分 ‎（Ⅱ）过作于，连，过作于，连，‎ 则有三垂线定理得面.即面面，‎ ‎∴面.故在面上的射影为.‎ ‎∴为直线与面所成的角.………………………………9分 依题意，..‎ 在中，,‎ 在中，,‎ ‎∴在中，.‎ ‎∴.………………………………………………………………12分 ‎20．解：（Ⅰ）依题意则，‎ 故椭圆的方程为 ………………………………………4分 ‎（Ⅱ）设：与交于，，‎ 得.‎ ‎.‎ ‎∴，， ………………………………………6分 ‎：，‎ 令得，‎ 同理： ………………………………………8分 ‎∴‎ ‎. ………………………………………12分 ‎21．解：（Ⅰ）对求导数得，‎ ‎∴， ………………………………………2分 在时，；在时，，‎ ‎∴在时取到极大值，也是最大值.‎ 所以的最大值为1‎ ‎（Ⅱ）证明：① 当，中有一个大于时，不妨设，‎ ‎∴，‎ ‎② 当，均属于区间时，设，，‎ ‎，‎ 同理，‎ ‎∴，‎ ‎∴.‎ ‎22．解：（Ⅰ）消去参数可得,因为，所以，所以曲线是在轴上方的部分，‎ 所以曲线的极坐标方程为，.…………………………………2分 曲线的直角坐标方程为………………………………5分 ‎（Ⅱ）设，则，直线的倾斜角为,则直线的参数方程为: (为参数). ……………………………7分 代入的直角坐标方程得,‎ 由直线参数方程中的几何意义可知=，‎ 因为，所以………………………10分 ‎23．解：（1）由得，即，.……………2分 所以解集为{x|或.} …………………………………5分 ‎ ‎（2）因为对任意，都有，使得=成立 所以，‎ 又，‎ 所以，‎ 从而 ……………………………10分