【数学】2020届一轮复习（文理合用）第7章第6讲空间向量及其运算(理)作业

【数学】2020届一轮复习（文理合用）第7章第6讲空间向量及其运算(理)作业

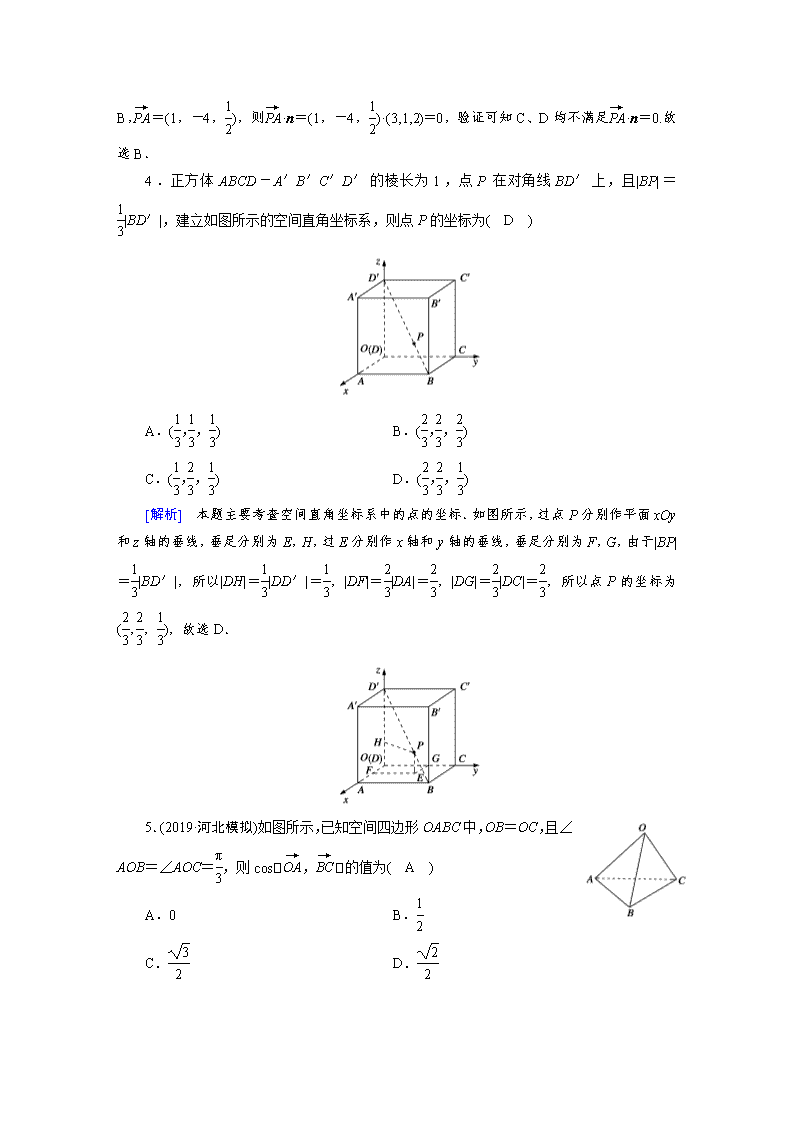
对应学生用书[练案51理]‎ 第六讲　空间向量及其运算(理)‎ A组基础巩固 一、选择题 ‎1．(2019·枣阳市第一中学月考)已知平面α，β的法向量分别为n1＝(2,3,5)，n2＝(－3,1，－4)，则(　C　)‎ A．α∥β　　　 B．α⊥β C．α，β相交但不垂直　　　 D．以上均不对 ‎[解析]　因为n1≠λn2，且n1·n2＝2×(－3)＋3×1＋5×(－4)＝－23≠0，所以α，β不平行，也不垂直．故选C．‎ ‎2．平行六面体ABCD－A1B1C1D1中，M为AC和BD的交点，若＝a，＝b，＝c，则下列式子中与相等的是(　C　)‎ A．－a＋b＋c B．a＋b－c C．－a＋b－c D．－a－b＋c ‎[解析]　＝＋＝－c＋＝－c＋(b－a)＝－a＋b－c.故选C．‎ ‎3．已知平面α内有一个点A(2，－1,2)，α的一个法向量为n＝(3,1,2)，则下列点P中，在平面α内的是(　B　)‎ A．(1，－1,1)　　　 B．(1,3，)‎ C．(1，－3，)　　　 D．(－1,3，－)‎ ‎[解析]　对于选项A，＝(1,0,1)，则·n＝(1,0,1)·(3,1,2)＝5≠0，故排除A；对于选项B，＝(1，－4，)，则·n＝(1，－4，)·(3,1,2)＝0，验证可知C、D均不满足·n＝0.故选B．‎ ‎4．正方体ABCD－A′B′C′D′的棱长为1，点P在对角线BD′上，且|BP|＝|BD′|，建立如图所示的空间直角坐标系，则点P的坐标为(　D　)‎ A．(，，)　　　 B．(，，)‎ C．(，，)　　　 D．(，，)‎ ‎[解析]　本题主要考查空间直角坐标系中的点的坐标．如图所示，过点P分别作平面xOy和z轴的垂线，垂足分别为E，H，过E分别作x轴和y轴的垂线，垂足分别为F，G，由于|BP|＝|BD′|，所以|DH|＝|DD′|＝，|DF|＝|DA|＝，|DG|＝|DC|＝，所以点P的坐标为(，，)，故选D．‎ ‎5．(2019·河北模拟)如图所示，已知空间四边形OABC中，OB＝OC，且∠AOB＝∠AOC＝，则cos，的值为(　A　)‎ A．0　　　 B． C．　　　 D． ‎[解析]　设＝a，＝b，＝c，由已知条件a，b＝a，c＝，且|b|＝|c|，·＝a·(c－b)＝a·c－a·b＝|a||c|－|a||b|＝0，所以cos，＝0，故选A．‎ ‎6．已知点A(2，－5,1)，B(2，－2,4)，C(1，－4,1)，则向量与的夹角为(　C　)‎ A．30°　　　 B．45°　　　‎ C．60°　　　 D．90°‎ ‎[解析]　由已知得＝(0,3,3)，＝(－1,1,0)，‎ 所以cos，＝＝＝.‎ 所以向量与的夹角为60°.故选C．‎ ‎7．(2019·晋江一模)设OABC是四面体，G1是△ABC的重心，G是OG1上的一点，且OG＝3GG1，若＝x＋y＋z，则(x，y，z)为(　A　)‎ A．(，，)　　　 B．(，，)‎ C．(，，)　　　 D．(，，)‎ ‎[解析]　如图所示，取BC的中点E，连接AE.‎ ＝＝(＋)＝＋ ‎＝＋(＋)‎ ‎＝＋(－＋－)‎ ‎＝(＋＋)．故选A．‎ ‎8.(2019·阳新县实验中学月考)如图所示，正方体ABCD－A′B′C′D′的棱长为1，E，F分别是BC，CD上的点，且BE＝CF＝a(0

查看更多