【数学】2020届一轮复习人教A版 几何证明选讲 课时作业 (1)

【数学】2020届一轮复习人教A版 几何证明选讲 课时作业 (1)

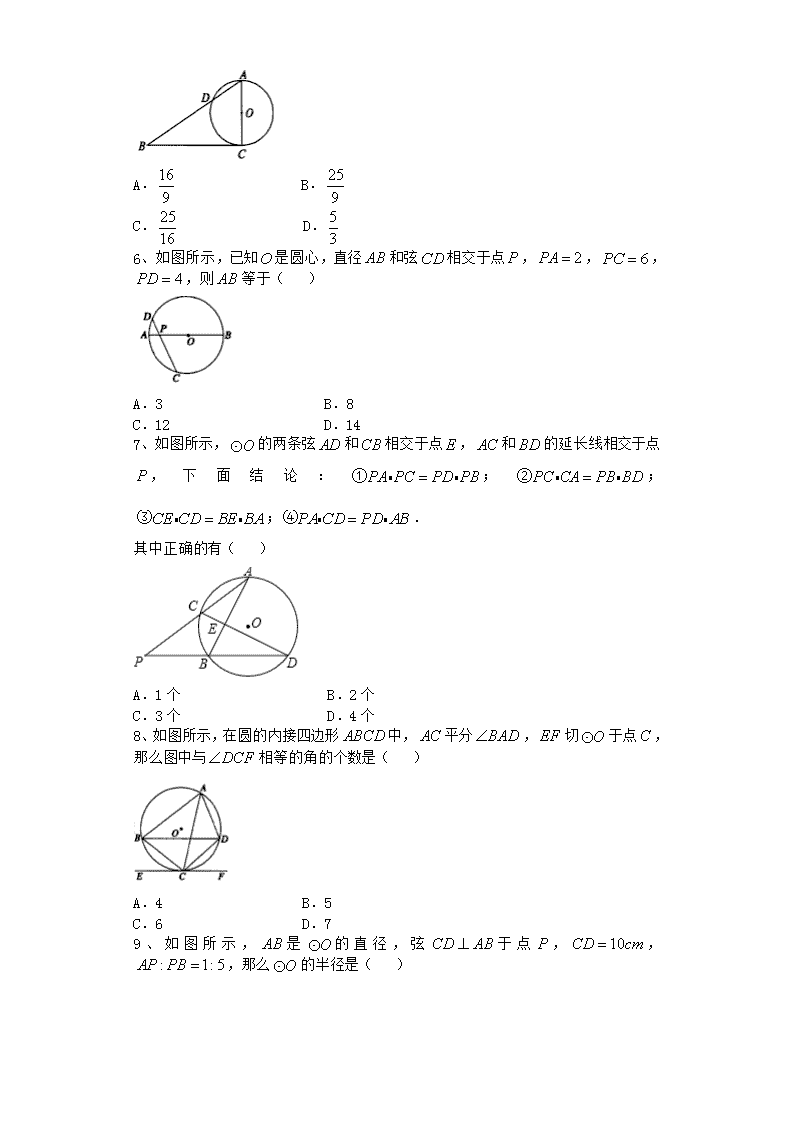
‎ 2020届一轮复习人教A版 几何证明选讲 课时作业 ‎1、如图所示，在中，弦与半径相交于点，且，，，则等于（ ）‎ A． B． ‎ C． D．‎ ‎2、圆内两条相交弦长，其中一弦长为，且被交点平分，另一条弦被交点分成1:4两部分，则这条弦长是（ ）‎ A． B． ‎ C． D．‎ ‎3、如图，切于，若，，，，则等于（ ）‎ A．3 B．4 ‎ C．6 D．8‎ ‎4、如图所示，切圆于，，直线交圆于，连接，且，于，，，则的值等于（ ）‎ A． B． ‎ C．2 D．4‎ ‎5、如图，已知的两条直角边的长分别为，，以为直径的圆与交于点，则（ ）‎ A． B． ‎ C． D．‎ ‎6、如图所示，已知是圆心，直径和弦相交于点，，，，则等于（ ）‎ A．3 B．8 ‎ C．12 D．14‎ ‎7、如图所示，的两条弦和相交于点，和的延长线相交于点，下面结论：；；；．‎ 其中正确的有（ ）‎ A．1个 B．2个 ‎ C．3个 D．4个 ‎8、如图所示，在圆的内接四边形中，平分，切于点，那么图中与相等的角的个数是（ ）‎ A．4 B．5 ‎ C．6 D．7‎ ‎9、如图所示，是的直径，弦于点，，，那么的半径是（ ）‎ A． B． ‎ C． D．‎ ‎10、如图所示，四边形是的内接四边形，延长到，已知，那么等于（ ）‎ A． B． ‎ C． D．‎ ‎11、如图所示，圆内接四边形的一组对边的延长线相交于点，对角线相交于点，则图中相似三角形共有（ ）‎ A．4对 B．2对 ‎ C．5对 D．3对 ‎12、如图所示，已知的半径为5，两弦相交于的中点，且，，则圆心到弦的距离为（ ）‎ A． B． ‎ C． D． 13、如图，是圆的直径，直线和圆相切于点，于，若，，则圆的面积是 ．‎ ‎14、如图，四边形是圆的内接四边形，延长和相交于点，若，则的值为 ．‎ ‎15、如图所示，为的直径，，是的半径，，点在上，，点是上一动点，则的最小值为 ．‎ ‎16、已知和内一点，过的直线交于两点，若，，则的半径长为 ．‎ ‎ 17、如图所示，内接于圆，切圆于是延长线上一点，连接交于点．若是的中点．求证：．‎ ‎18、如图所示，已知圆外有一点，作圆的切线为切点，过的中点作割线,交圆于两点，连接PA并延长，交圆于点连接交圆于点,若．‎ ‎（1）求证：；‎ ‎（2）求证：四边形是平行四边形．‎ ‎19、已知中，，为外接原劣弧上的点（不与点、重合），延长至，延长交的延长线于．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求证：．‎ ‎20、已知中，，为外接原劣弧上的点（不与点、重合），延长至，延长交的延长线于．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求证：．‎ 参考答案 ‎1、答案：D 由题设可得,即,也即,故应选D．‎ 考点：相交弦定理的灵活运用．‎ ‎【易错点晴】圆是平面几何中的重要代表曲线之一,也是高中数学的重要内容和高考必考的重要考点．本题以圆与直线的位置关系的条件为背景,考查的是相交弦定理等有关知识和方法的综合运用．解答时先依据题设所在弦被点分成的线段长分别为,再用相交弦定理建立方程求得,从而使得问题巧妙获解．‎ ‎2、答案：C 设所求弦长为,由题设及相交弦定理可得,即,则该弦长为,故应选C．‎ 考点：相交弦定理及运用．‎ ‎【易错点晴】圆是平面几何中的重要代表曲线之一,也是高中数学的重要内容和高考必考的重要考点．本题以圆与直线的位置关系的条件为背景,考查的是相交弦定理等有关知识和方法的综合运用．解答时先设所求弦长为,再用相交弦定理建立方程求得,从而使得问题巧妙获解．‎ ‎3、答案：C ‎ 由切割线定理可得；由切割线定理可得．因,故．故应选C．‎ 考点：切割线定理及运用．‎ ‎【易错点晴】圆是平面几何中的重要代表曲线之一,也是高中数学的重要内容和高考必考的重要考点．本题以圆与直线的位置关系满足的条件为背景,考查的是切割线定理与相似三角形的性质等有关知识和方法的综合运用．解答时先用切割线定理求得,再运用相似三角形的对应边成比例这一性质建立方程求得,从而使得问题巧妙获解．‎ ‎4、答案：B ‎ 由切割线定理可得,因,故应选B．‎ 考点：解直角三角形及切割线定理的运用．‎ ‎5、答案：A 因,故,由切割线定理可得,则,故．故应选A．‎ 考点：勾股定理、切割线定理及运用．‎ ‎6、答案：D 设,由相交弦定理可得,故,应选D．‎ 考点：相交弦定理及运用．‎ ‎7、答案：A 由切割线定理可得,故在上述答案中只有正确．故应选A．‎ 考点：圆幂定理及运用．‎ ‎8、答案：B 因,,故应选B．‎ 考点：弦切角等于同弦所对圆周角,同弧所对圆周角相等．‎ ‎9、答案：C ‎ 设,则,由题设,即,故．故应选C．‎ 考点：垂径定理及运用．‎ ‎10、答案：C 设,则,故.故应选C.‎ 考点：圆内接四边形的内角之间的关系及运用.‎ ‎11、答案：A 因,,故共有对,应选A.‎ 考点：相似三角形的判定.‎ ‎12、答案：A 由题设,因圆的半径，，故,又因，故又相交弦定理可得，即，则，设的中点为，则，所以.故应选A.‎ 考点：相交弦定理及垂径定理的综合运用.‎ ‎13、答案：‎ 由弦切角定理可得,在中, 因,故,故圆的面积为．故应填答案．‎ 考点：弦切角定理及含的直角三角形的性质及运用．‎ ‎【易错点晴】圆是平面几何中的重要代表曲线之一,也是高中数学的重要内容和高考必考的重要考点．本题以圆与直线的位置关系的条件为背景,考查的是弦切角与其所对的圆周角相等这一定理和解直角三角形等有关知识和方法的综合运用．解答时先依据题设运用弦切角与其所对的圆周角相等,求出,再运用在直角三角形中所对的直角边是斜边的一半这一结论求出,进而运用圆的面积公式求得其面积为,从而使得问题巧妙获解．‎ ‎14、答案：‎ 设,由割线定理可得,即,所以．故应填答案．‎ 考点：割线定理及运用．‎ ‎【易错点晴】圆是平面几何中的重要代表曲线之一,也是高中数学的重要内容和高考必考的重要考点．本题以圆与直线的位置关系的条件为背景,考查的是割线定理及相似三角形的性质等有关知识和方法的综合运用．解答时先设,然后再依据题设运用割线定理可得求得,再运用相似三角形的性质求得,从而使得问题巧妙获解．‎ ‎15、答案：‎ 由题意可得,则,又点关于对称,故,故应填答案．‎ 考点：圆的对称性及连接两点之间的线段最短及运用．‎ ‎16、答案：‎ 由题意可得,解之得,故应填答案．‎ 考点：相交弦定理及灵活运用．‎ ‎17、答案：试题分析：借助题设条件运用相似三角形的性质及圆幂定理推证．‎ 试题 过作交的延长线于点．‎ ‎，，‎ ‎（等价于）．‎ 又是圆的切线，．‎ 又，，‎ ‎，，‎ ‎∽．‎ ‎，，‎ 即．‎ 考点：相似三角形的性质及圆幂定理等有关知识的综合运用． 18、答案：试题分析：（1）由切割线定理，及是的中点，可得，进而，结合，可得，则，即；再由，可得，再由等角的补角相等可得，进而得到；‎ ‎（2）由，可得，即；由，是圆的切线，可证得，即；再由平行四边形的判定定理得到四边形是平行四边形．‎ 试题 ‎（1）是圆的切线，是圆的割线，是的中点，‎ ‎，又，‎ 即．‎ ‎（2）,‎ 即是圆的切线，‎ ‎，‎ 即四边形是平行四边形．‎ 考点：（1）与圆有关的比例线段；（2）相似三角形的判定． 19、答案：试题分析：（I）根据四点共圆，有，而等腰对等角，由此求得；（II）由（I）知，所以，根据割线定理得，两式联立可证得.‎ 试题 ‎（I）证明：、、、四点共圆 ‎．‎ 且，‎ ‎，‎ ‎（II）由（I）得，又，‎ 所以与相似，‎ ‎，‎ 又，，‎ 根据割线定理得，‎ ‎．‎ 考点：几何证明选讲． 20、答案：试题分析：（I）根据四点共圆，有，而等腰对等角，由此求得；（II）由（I）知，所以，根据割线定理得，两式联立可证得.‎ 试题 ‎（1）证明：、、、四点共圆 ‎．‎ 且，‎ ‎，‎ ‎（2）由（1）得，又，‎ 所以与相似，‎ ‎，‎ 又，，‎ 根据割线定理得，‎ ‎．‎ 考点：几何证明选讲． ‎