- 2021-06-15 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教A版排列与排列数公式课时作业
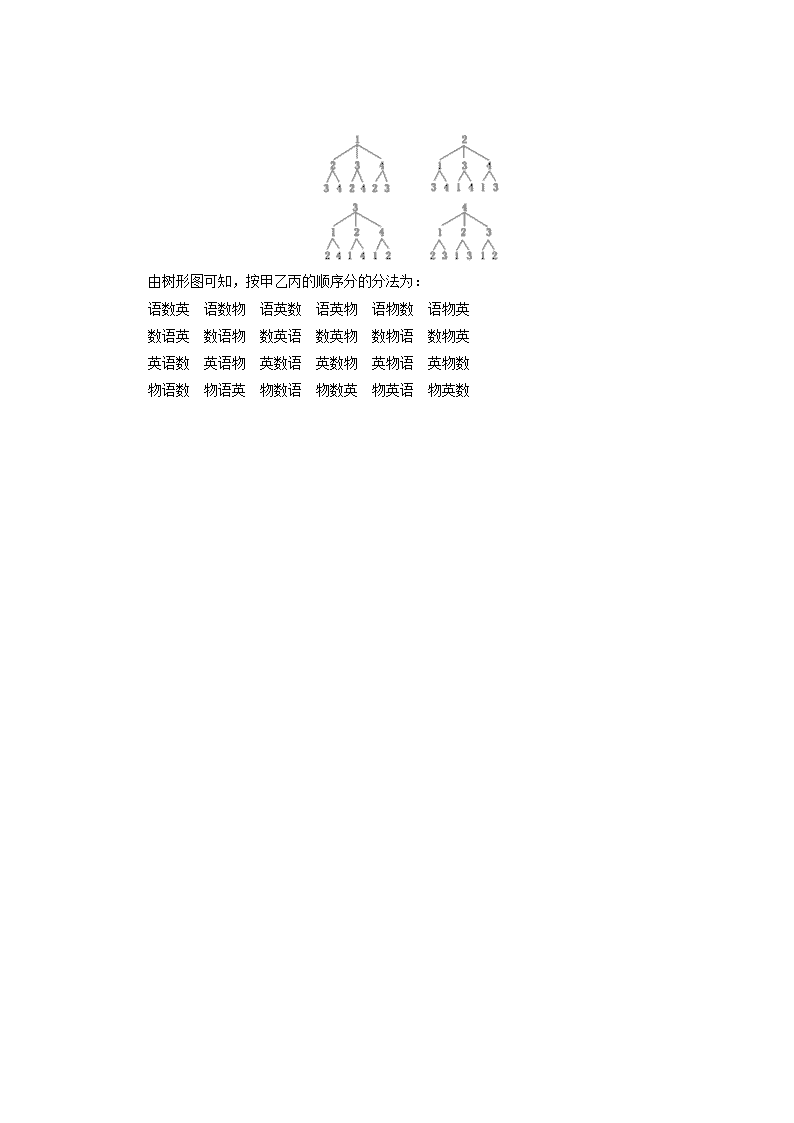
1.5A+4A等于( ) A.107 B.323 C.320 D.348 2.等于( ) A. B. C. D. 3.设a∈N+,且a<27,则(27-a)(28-a)·…·(34-a)等于( ) A.A B.A C.A D.A 4.若从4名志愿者中选出2人分别从事翻译、导游两项不同工作,则选派方案共有( ) A.16种 B.6种 C.15种 D.12种 5.已知9!=362 880,那么A=________. 6.给出下列问题: ①从1,3,5,7这四个数字中任取两数相乘,可得多少个不同的积? ②从2,4,6,7这四个数字中任取两数相除,可得多少个不同的商? ③有三种不同的蔬菜品种,分别种植在三块不同的试验田里,有多少种不同的种植方法? ④有个头均不相同的五位同学,从中任选三位同学按左高右低的顺序并排站在一排照相,有多少种不同的站法? 上述问题中,是排列问题的是________.(填序号) 7.(1)计算; (2)解方程3A=4A. 8.从语文、数学、英语、物理4本书中任意取出3本分给甲、乙、丙三人,每人一本,试将所有不同的分法列举出来. 答案 1.选D 原式=5×5×4×3+4×4×3=348. 2.选C ==. 3.选D 8个括号里面是连续的自然数,依据排列数的概念,选D. 4.选D 4名志愿者分别记作甲、乙、丙、丁,则选派方案有:甲乙,甲丙,甲丁,乙甲,乙丙,乙丁,丙甲,丙乙,丙丁,丁甲,丁乙,丁丙,即共有A=12种方案. 5.解析:A===181 440. 答案:181 440 6.解析:对于①,任取两数相乘,无顺序之分,不是排列问题;对于②,取出的两数,哪一个作除数,哪一个作被除数,其结果不同,与顺序有关,是排列问题;对于③,三种不同的蔬菜品种任一种种植在不同的试验田里,结果不同,是排列问题;对于④,选出的三位同学所站的位置已经确定,不是排列问题. 答案:②③ 7.解:(1)原式====. (2)由3A=4A,得=,化简, 得x2-19x+78=0,解得x1=6,x2=13. 又∵x≤8,且x-1≤9,∴原方程的解是x=6. 8.解:从语文、数学、英语、物理4本书中任意取出3本,分给甲、乙、丙三人,每人一本,相当于从4个不同的元素中任意取出3个元素,按“甲、乙、丙”的顺序进行排列,每一个排列就对应着一种分法,所以共有A=4×3×2=24种不同的分法. 不妨给“语文、数学、英语、物理”编号,依次为1,2,3,4号,画出下列树形图: 由树形图可知,按甲乙丙的顺序分的分法为: 语数英 语数物 语英数 语英物 语物数 语物英 数语英 数语物 数英语 数英物 数物语 数物英 英语数 英语物 英数语 英数物 英物语 英物数 物语数 物语英 物数语 物数英 物英语 物英数查看更多