- 2021-06-12 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习教案: 幂函数与二次函数
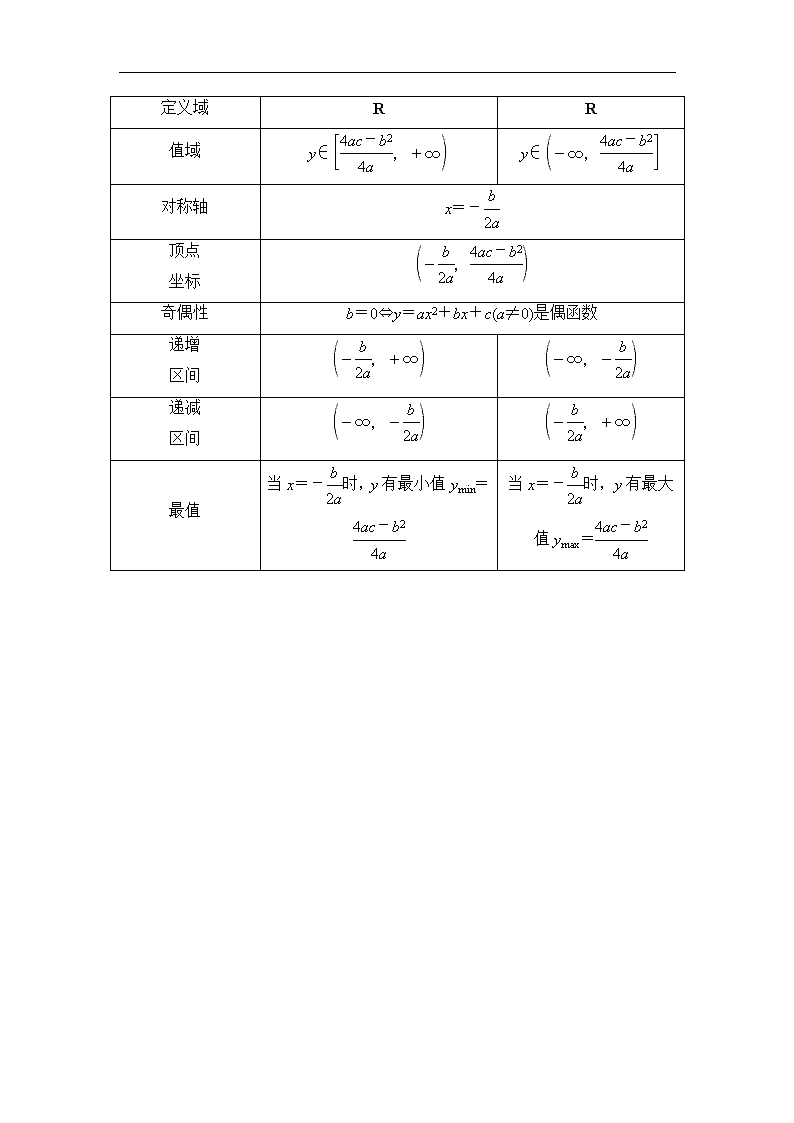
幂函数与二次函数 主标题:幂函数与二次函数 副标题:为学生详细的分析幂函数与二次函数的高考考点、命题方向以及规律总结。 关键词:幂函数,二次函数 难度:3 重要程度:5 考点剖析: 1.了解幂函数的概念. 2.结合函数y=x,y=x2,y=x3,y=,y=的图象,了解它们的变化情况. 3.理解并掌握二次函数的定义、图象及性质. 4.能用二次函数、方程、不等式之间的关系解决简单问题. 命题方向:高考对该部分的考查多与二次函数相结合综合命题,涉及函数零点问题,比较方程根的大小问题,函数值的求解,函数图象的识别等问题,考查学生分析、解决问题的能力. 规律总结:1.对于幂函数的图象的掌握只要抓住在第一象限内三条线分第一象限为六个区域,即x=1,y=1,y=x分区域.根据α<0,0<α<1,α=1,α>1的取值确定位置后,其余象限部分由奇偶性决定. 2.二次函数的综合应用多涉及单调性与最值或二次方程根的分布问题,解决的主要思路是等价转化,多用到数形结合思想与分类讨论思想. 3.对于与二次函数有关的不等式恒成立或存在问题注意等价转化思想的运用. 知 识 梳 理 1.幂函数 (1)幂函数的定义 一般地,形如y=xα的函数称为幂函数,其中x是自变量,α为常数. (2)常见的5种幂函数的图象 (3)常见的5种幂函数的性质 函数 特征 性质 y=x y=x2 y=x3 y=x y=x-1 定义域 R R R [0,+∞) {x|x∈R,且x≠0} 值域 R [0,+∞) R [0,+∞) {y|y∈R,且y≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增 (-∞,0]减,[0,+∞)增 增 增 (-∞,0)减,(0,+∞)减 定点 (0,0),(1,1) (1,1) 2.二次函数 (1)二次函数的定义 形如f(x)=ax2+bx+c(a≠0)的函数叫做二次函数. (2)二次函数的三种常见解析式 ①一般式:f(x)=ax2+bx+c(a≠0); ②顶点式:f(x)=a(x-m)2+n(a≠0),(m,n)为顶点坐标; ③两根式:f(x)=a(x-x1)(x-x2)(a≠0)其中x1,x2分别是f(x)=0的两实根. (3)二次函数的图象和性质 函数 二次函数y=ax2+bx+c(a,b,c是常数,a≠0) 图象 a>0 a<0 定义域 R R 值域 y∈ y∈ 对称轴 x=- 顶点 坐标 奇偶性 b=0⇔y=ax2+bx+c(a≠0)是偶函数 递增 区间 递减 区间 最值 当x=-时,y有最小值ymin= 当x=-时,y有最大值ymax=查看更多