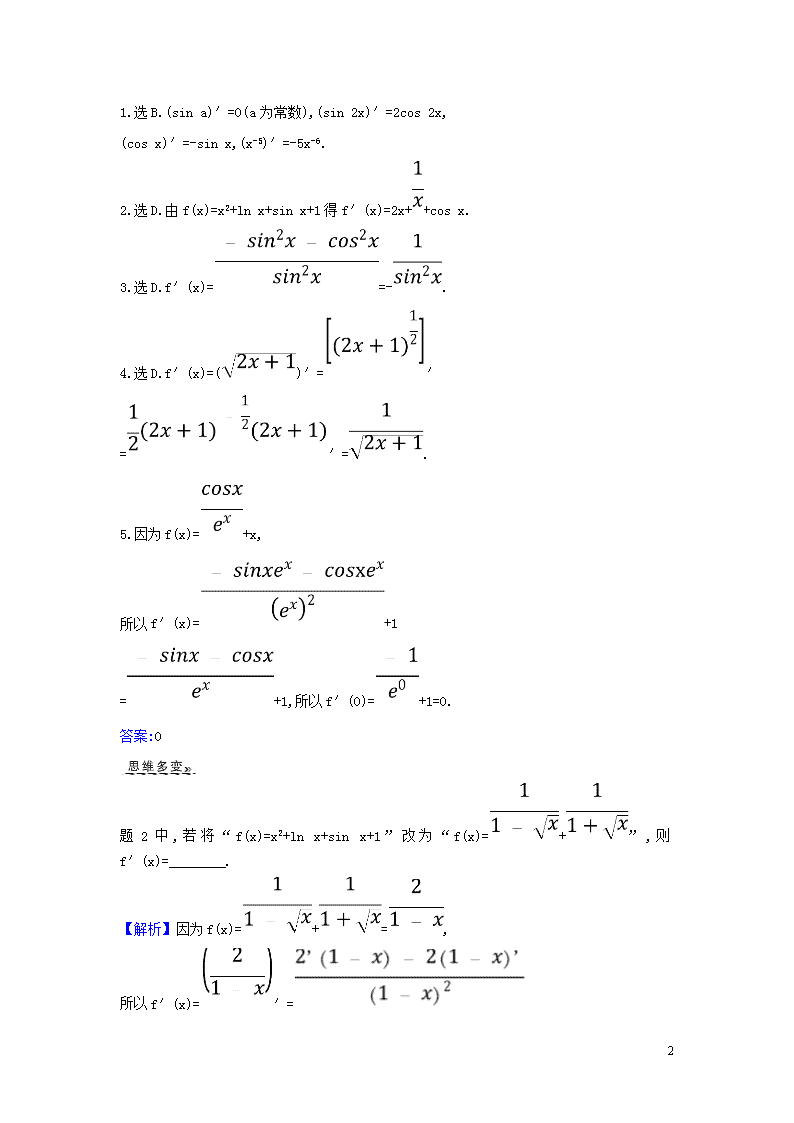2021版高考数学一轮复习第三章导数及其应用3-1导数及导数的运算练习新人教B版

2021版高考数学一轮复习第三章导数及其应用3-1导数及导数的运算练习新人教B版

‎3.1 导数及导数的运算 核心考点·精准研析 考点一　导数的计算 ‎ ‎1.下列求导运算正确的是 (　　)‎ A.(sin a)′=cos a(a为常数) ‎ B.(sin 2x)′=2cos 2x C.(cos x)′=sin x D.(x-5)′=- x-6‎ ‎2.函数f(x)=x2+ln x+sin x+1的导函数f′(x)= (　　)‎ A.2x++cos x+1 B.2x-+cos x C.2x+-cos x　　 D.2x++cos x ‎3.函数f(x)=的导函数f′(x)= (　　)‎ A.tan x　 B.- C.- D.-‎ ‎4.函数f(x)=的导函数f′(x)= (　　)‎ A.2　 B.‎ C. D.‎ ‎5.设f′(x)是函数f(x)=+x的导函数,则f′(0)的值为________.  ‎ ‎【解析】‎ 10‎ ‎1.选B.(sin a)′=0(a为常数),(sin 2x)′=2cos 2x,‎ ‎(cos x)′=-sin x,(x-5)′=-5x-6.‎ ‎2.选D.由f(x)=x2+ln x+sin x+1得f′(x)=2x++cos x.‎ ‎3.选D.f′(x)==-.‎ ‎4.选D.f′(x)=()′=′‎ ‎=′=.‎ ‎5.因为f(x)=+x,‎ 所以f′(x)=+1‎ ‎=+1,所以f′(0)=+1=0.‎ 答案:0‎ 题2中,若将“f(x)=x2+ln x+sin x+1”改为“f(x)=+”,则f′(x)=________. ‎ ‎【解析】因为f(x)=+=,‎ 所以f′(x)=′=‎ 10‎ ‎=.‎ 答案:‎ ‎【秒杀绝招】　‎ 排除法解T3, 根据sin x=0时f(x)无意义,所以f′(x)也无意义排除A,C,‎ cos x=0时f(x)有意义,所以f′(x)也应有意义排除B.‎ 考点二　导数的简单应用 ‎ ‎【典例】1.若函数f(x)=eax+ln(x+1),f′(0)=4,则a=________. ‎ ‎2.已知函数f(x)的导函数为f′(x),且f(x)=2xf′(e)-ln x,则f′(e)=________. ‎ ‎3.(2020·宝鸡模拟)二次函数y=f(x)的图象经过坐标原点,若其导函数为f′(x)=3x-,则f(x)=______.  ‎ ‎【解题导思】‎ 序号 联想解题 ‎1‎ 由f′(0)=4,想到求f′(x),列方程 10‎ ‎2‎ 由f′(e)想到求f′(x)并代入x=e ‎3‎ 由二次函数y=f(x)的图象经过坐标原点,想到设函数的解析式为f(x)=ax2+bx ‎【解析】‎ ‎1.由f(x)=eax+ln(x+1),‎ 得f′(x)=aeax+,‎ 因为f′(0)=4,所以f′(0)=a+1=4,所以a=3.‎ 答案:3‎ ‎2.因为f(x)=2xf′(e)-ln x,‎ 所以f′(x)=2f′(e)-,令x=e得:‎ f′(e)=2f′(e)-,即f′(e)=.‎ 答案:‎ ‎3.根据题意,二次函数y=f(x)的图象经过坐标原点,设其解析式为f(x)=ax2+bx,‎ 则有f′(x)=2ax+b,‎ 又由f′(x)=3x-,得2ax+b=3x-,‎ 则a=,b=-,故f(x)=x2-x.‎ 答案:x2-x ‎　含参数的函数的导数要注意的两点 ‎(1)含有字母参数的函数求导时,要分清哪是变量哪是参数,参数是常量,其导数为零.‎ 10‎ ‎(2)注意利用题目条件构建方程,求出参数的值.此时要注意区别函数f(x)及其导数f′(x).‎ ‎1.已知f(x)的导函数为f′(x),且满足f(x)=x3+f′x2-x,则f(1)=(　　)‎ A.-2 B.2 C.-1 D.1‎ ‎【解析】选C.由f(x)=x3+f′x2-x,得 f′(x)=3x2+2f′x-1,‎ 所以f′=+ f′-1,所以f′=-1,f(x)=x3-x2-x,‎ 所以f(1)=13-12-1=-1.‎ ‎2.函数f(x)=ln x+a的导函数为f′(x),若方程f′(x)=f(x)的根x0小于1,则实数a的取值范围为 (　　)‎ A.(1,+∞) B.(0,1)‎ C.(1,) D.(1,)‎ ‎【解析】选A.由函数f(x)=ln x+a可得f′(x)=,由于使得f′(x0)=f(x0)成立的01,ln x0<0,所以a=-ln x0>1,故有a>1.‎ 考点三　导数几何意义的运用 ‎ 命 题 精 考什么:(1)求切线方程、求切点坐标、与切线有关求参数的值或取值范围.(2)考查数学运算、直观想象、逻辑推理的核心素养 怎么考:‎ 10‎ 解 读 与直线的方程、不等式等结合考查直线的斜率、直线的点斜式方程、导数的几何意义等问题 新趋势:以三角函数、指数函数、对数函数为载体,与求导数和导数的几何意义交汇考查.‎ 学 霸 好 方 法 ‎1.注意两类切线问题的区别 ‎(1)“过”与“在”:曲线y=f(x)“在点P(x0,y0)处的切线”与“过点P(x0,y0)的切线”的区别:前者P(x0,y0)为切点,而后者P(x0,y0)不一定为切点.‎ ‎(2)“切点”与“公共点”:某曲线的切线与此曲线的公共点有可能有多个(即除了切点之外可能还有其他公共点).‎ ‎2.利用导数求曲线的切线方程 ‎ 若已知曲线y=f(x)过点P(x0,y0),求曲线过点P的切线方程,则需分点P(x0,y0)是切点和不是切点两种情况求解.‎ ‎(1)当点P(x0,y0)是切点时,切线方程为 y-y0=f ′(x0)(x-x0).‎ ‎(2)当点P(x0,y0)不是切点时,可分以下几步:‎ 第一步:设出切点坐标P′(x1, f(x1)); ‎ 第二步:写出曲线在点P′(x1, f(x1))处的切线方程y-f(x1)=f ′(x1)(x ‎-x1); ‎ 第三步:将点P的坐标(x0,y0)代入切线方程求出x1; ‎ 第四步:将x1的值代入方程y-f(x1)=f′(x1)(x-x1),可得过点P(x0,y0)的切线方程.‎ 已知切点求切线的方程问题 ‎【典例】(2019·全国卷Ⅰ)曲线y=3(x2+x)ex在点(0,0)处的切线方程为____________. ‎ ‎【解析】y′=3(2x+1)ex+3(x2+x)ex=3(x2+3x+1)ex,所以k=y′|x=0=3,‎ 所以曲线y=3(x2+x)ex在点(0,0)处的切线方程为y=3x,即3x-y=0.‎ 答案:3x-y=0‎ 用导数的几何意义求曲线的切线方程的关键是什么?‎ 提示:关键是确定切点坐标.‎ 未知切点求切线的方程问题 ‎【典例】已知函数f(x)=x3+x-16,若直线l为曲线y=f(x)的切线,且经过原点,则直线l的方程为________. ‎ 10‎ ‎【解析】设切点坐标为(x0,y0),‎ 则直线l的斜率为f′=3+1,‎ 所以直线l的方程为 y=(3+1)(x-x0)++x0-16,‎ 因为直线l过原点,‎ 所以0=(3+1)(0-x0)++x0-16,‎ 整理得,=-8,所以x0=-2,‎ 所以y0= (-2)3+(-2)-16=-26,‎ f′=3×(-2)2+1=13.‎ 所以直线l的方程为y=13x.‎ 答案:y=13x 如何从题目条件判断是否知道切点?‎ 提示:从题目条件的叙述方式判断,一般来说,“过××点”的切线,都是不知道切点.知道切点的叙述方式为“在××点处的切线”.‎ 求参数的值 ‎【典例】(2019·全国卷Ⅲ)已知曲线y=aex+xln x在点(1,ae)处的切线方程为y=2x+b,则 (　　)‎ A.a=e,b=-1 B.a=e,b=1‎ C.a=e-1,b=1 D.a=e-1,b=-1‎ ‎【解析】选D.令f(x)=aex+xln x,‎ 则f′(x)=aex+ln x+1,f′(1)=ae+1=2,得a==e-1.‎ f(1)=ae=2+b,可得b=-1.‎ 切线问题中可以用来列出等量关系的依据有哪些?‎ 提示:(1)切点处的导数为切线斜率;‎ 10‎ ‎(2)切点在切线上;‎ ‎(3)切点在曲线上.‎ ‎1.已知定义在R上的奇函数f(x),当x≤0时,f(x)=x3-2x-m,则曲线在点P(2,f(2))处的切线斜率为 (　　)‎ A.10　 B.-10　‎ C.4 D.与m的取值有关 ‎【解析】选A.因为函数f(x)是定义在R上的奇函数,‎ 所以f(0)=0,即f(0)=-m =0,所以m =0,‎ 即当x≤0时,f(x)=x3-2x,‎ 当x>0时,f(x)=-f(-x)= x3-2x,‎ 所以当x>0时,f′(x)=3x2-2,f′(2)=3×22-2=10.‎ ‎2.(2019·吉安模拟)已知过点P(1,1)且与曲线y=x3相切的直线的条数有(　　)‎ A.0 B.1 C.2 D.3‎ ‎【解析】选C.若直线与曲线相切于点(x0,y0)(x0≠0),‎ 则k===+x0+1,‎ 因为y′=3x2,所以=3,‎ 所以3=+x0+1,所以2-x0-1=0,‎ 所以x0=1或x0=-,‎ 所以过点P(1,1)与曲线y=x3相切的直线方程为3x-y-2=0或3x-4y+1=0,所以共有2条.‎ ‎3.(2020·十堰模拟)若直线y=12x+m与曲线y=x3-2相切,则m=________. ‎ ‎【解析】y=x3-2的导数为y′=3x2,直线y=12x+m与曲线y=x3-2相切,‎ 设切点为(s,t),可得3s2=12,12s+m=s3-2,即有s=2,m=-18;s=-2,m=14.‎ 答案:14或-18‎ 10‎ ‎1.设点P是曲线y=x3-x+上的任意一点,则曲线在点P处切线的倾斜角α的取值范围为 (　　)‎ A.∪ B.‎ C.∪ D.‎ ‎【解析】选C.因为y′=3x2-≥-,故切线的斜率k≥-,所以切线的倾斜角α的取值范围为∪.‎ ‎2.如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),则曲线g(x)在x=3处的切线方程为________. ‎ ‎【解析】由题图可知曲线y=f(x)在x=3处的切线斜率等于-,即f′(3)=-.又g(x)=xf(x),所以g′(x)=f(x)+xf′(x),g′(3)=f(3)+3f′(3),由题图可知f(3)=1,所以g(3)=3f(3)=3,g′(3)=1+3×=0,则曲线g(x)在x=3处的切线方程为y-3=0.‎ 答案:y-3=0‎ ‎3.阅读材料:求函数y=ex的导函数.‎ 解:因为y=ex,所以x=ln y,‎ 所以x′=′,所以1=·y′,所以y′=y=ex.‎ 10‎ 借助上述思路,曲线y=,x∈在点(1,1)处的切线方程为__________. ‎ ‎【解析】因为y=,‎ 所以ln y=ln,‎ 所以·y′=ln+,‎ 所以y′=,‎ 当x=1时,y′=4,‎ 所以曲线y=,x∈在点(1,1)处的切线方程为y-1=4,即y=4x-3.‎ 答案:y=4x-3‎ 10‎