2020届高三数学适应性练习

2020届高三数学适应性练习

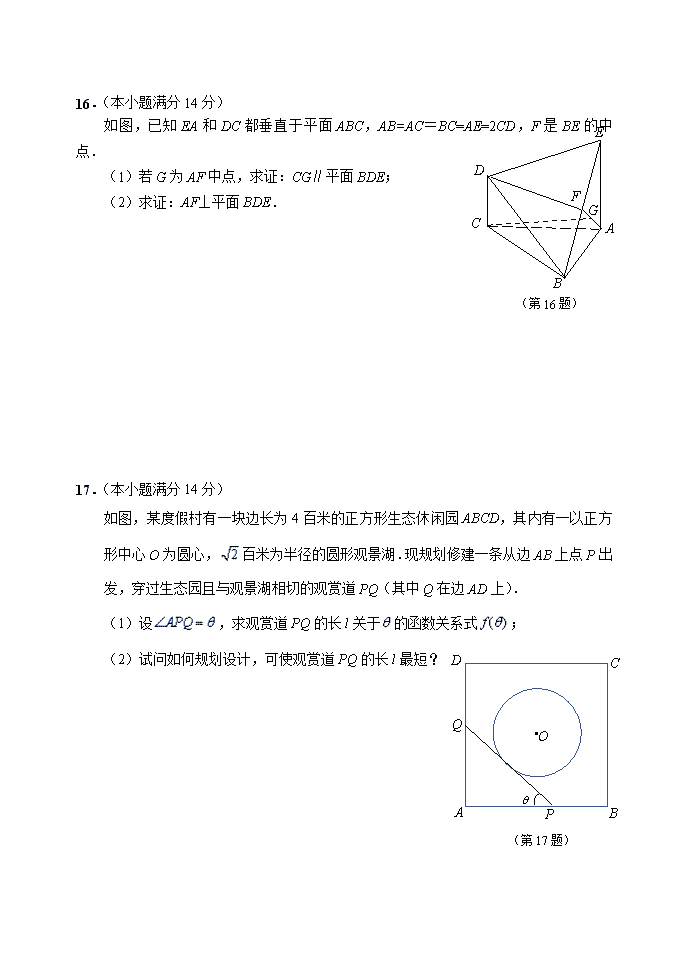
‎2020届高三数学适应性练习 参考公式：‎ 样本数据的方差，其中．‎ 一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．‎ I ← 1‎ While I < 6‎ ‎ I ← I +2‎ ‎ S ←2I +3‎ End While Print S ‎（第4题）‎ ‎1． 已知集合，，则集合= ．‎ ‎2． 已知复数（i为虚数单位），则复数z的模为 .‎ ‎3． 现有5位病人，他们服用某种药物后的康复时间（单位：天）记录 如下：10，11，12，13，14，则康复时间的方差为 .‎ ‎4． 一个算法的伪代码如图所示，执行此算法，则最后输出的的值 是 ．‎ ‎5． 一张方桌有四个座位，A先坐在如图所示的座位上，B，C，D三人随机坐到其他三个位置上，则A与B相对而坐的概率为 ．‎ ‎（第5题）‎ ‎（第6题）‎ ‎6． 已知向量在正方形网格中的位置如图所示．若，则的值为 ．‎ ‎7． 将函数的图象向右平移个单位长度，所得函数为偶函数，则的最小正值是 ．‎ ‎8． 已知是等比数列，是其前项和．若，，则的值为 ．‎ ‎9． 过双曲线的右焦点F作渐近线的垂线，垂足为P．若△POF的面积为，则该双曲线的离心率为 ． ‎ ‎10．已知直线经过点，则的最小值是 ．‎ ‎11．过年了，小张准备去探望奶奶，到商店买了一盒点心．为了美观起见，售货员用彩绳对点心盒做了一个捆扎（如图（1）所示），并在角上配了一个花结．彩绳与长方体点心盒均相交于棱的四等分点处．设这种捆扎方法所用绳长为l1，一般的十字捆扎（如图（2）所示）所用绳长为l2．若点心盒的长、宽、高之比为2:2:1，则的值为 ．‎‎（第11题）‎ ‎12．已知函数，则不等式的解集是 ．‎ ‎（第14题）‎ ‎13．已知A(x1，y1)、B(x2，y2)为圆M：上的两点，且，设为弦AB的中点，则的最小值为 ．‎ ‎14．已知等边的边长为1，点D，E，F分别在边AB，BC，AC上，且．若AD=x，CE=y，则的取值范围为 ．‎ 二、解答题：本大题共6小题，共计90分． ‎ ‎15．（本小题满分14分）‎ 在中，角所对的边分别为a，b，c，．‎ ‎（1）若面积为，求ab的值；‎ ‎（2）若，求．‎ ‎16．（本小题满分14分）‎ G ‎（第16题）‎ B D F E C A 如图，已知EA和DC都垂直于平面ABC，AB=AC＝BC=AE=2CD，F是BE的中点．‎ ‎（1）若G为AF中点，求证：CG∥平面BDE；‎ ‎（2）求证：AF⊥平面BDE．‎ ‎17．（本小题满分14分）‎ 如图，某度假村有一块边长为4百米的正方形生态休闲园ABCD，其内有一以正方形中心O为圆心，百米为半径的圆形观景湖．现规划修建一条从边AB上点P出发，穿过生态园且与观景湖相切的观赏道PQ（其中Q在边AD上）．‎ ‎（1）设，求观赏道PQ的长l关于的函数关系式；‎ ‎（第17题）‎ P Q O A B C D ‎（2）试问如何规划设计，可使观赏道PQ的长l最短？‎ ‎18．（本小题满分16分）‎ 如图，在平面直角坐标系xOy中，已知椭圆的离心率为，点在椭圆上．若直线l与椭圆有且只有一个公共点，且l与直线相交于．‎ ‎（第18题）‎ P O x y Q ‎（1）求椭圆的方程； ‎ ‎（2）当直线l的斜率为时，求直线的方程；‎ ‎（3）点T是x轴上一点，若总有，‎ 求T点坐标．‎ ‎19．（本小题满分16分）‎ 设数列{an}的前n项和为Sn，且满足，，．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）记，．‎ ‎① 求Tn；‎ ‎② 求证：． ‎ ‎20．（本小题满分16分）‎ 已知函数，．‎ ‎（1）若函数f(x)与g(x)在上均单调递减，求实数a的取值范围；‎ ‎（2）当（其中e为自然对数的底数）时，记函数的最小值为m．‎ 求证：；‎ ‎（3）记，若函数h(x)有两个不同零点，求实数a 的取值范围．‎ ‎2020届高三数学适应性练习 附加 ‎21．【选做题】本题包括A、B、C三小题，请选定其中两题，并在答题卡相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．‎ A．[选修4-2：矩阵与变换]（本小题满分10分）‎ 已知，矩阵的特征值所对应的一个特征向量为．‎ ‎（1）求矩阵；‎ ‎（2）若曲线：在矩阵对应的变换作用下得到另一曲线，‎ 求曲线的方程．‎ B．[选修4-4：坐标系与参数方程]（本小题满分10分）‎ 在平面直角坐标系中，已知直线l的参数方程为（t为参数）．在以坐标原点为极点，轴正半轴为极轴的极坐标系中，曲线的极坐标方程为，求直线l被曲线截得的弦长．‎ C．[选修4-5：不等式选讲]（本小题满分10分）‎ 已知x，y，z是正实数，且，求证：．‎ ‎【必做题】第22、23题，每小题10分，共计20分．请在答题卡指定区域内作答，解答时应写出 文字说明、证明过程或演算步骤．‎ ‎22．(本小题满分10分)‎ 如图，在平面直角坐标系xOy中， 已知点A（0，1），点B在直线上，点T满足∥，，T点的轨迹为曲线C．‎ ‎（1）求曲线C的方程；‎ ‎（2）过点P的直线交曲线C于点，分别过M，N作直线l的垂线，垂足分别为．‎ ① 若，求实数t的值；‎ ② 点关于轴的对称点为（与不重合），求证：直线过一定点，并求出x y A T B O ‎（第22题）‎ 这个定点的坐标．‎ ‎23．(本小题满分10分)‎ ‎ 已知数列满足：．‎ ‎（1）证明：；‎ ‎（2）证明：．‎ 参考答案及评分细则 一、填空题：本大题共14小题，每小题5分，共计70分． ‎ ‎1． ； 2． ； 3． 2； 4． 17；‎ ‎5． ； 6． 0； 7． ； 8． ；‎ ‎9． ； 10． 32； 11． ； 12． ；‎ ‎13．； 14． ．‎ 二、解答题：本大题共6小题，共计90分． ‎ ‎15．【解】（1）因为 ，‎ 在中，由正弦定理，‎ 得，化简得， ……3分 在中，由余弦定理得，， ……4分 因为，所以，‎ 又面积为 ，可得，所以. ……7分 ‎（2）因为,‎ 在中，由正弦定理,所以 因为，所以 ……9分 由（1）得，所以，‎ 化简得，所以. ……11分 因为，所以，‎ 所以，‎ 所以. ……14分 ‎16．（本小题满分14分）‎ 证明：（1）取EF中点Q，连结GQ，‎ ‎ 因为G为AF中点，‎ ‎ 所以GQ∥AE，且. ……2分 ‎ 因为EA和DC都垂直于平面ABC，‎ ‎ 所以CD∥AE，又AE=2CD，‎ ‎ 所以GQ∥CD，且.‎ ‎ 所以四边形CDQG为平行四边形，‎ ‎ 所以CG∥DQ， ……4分 ‎ 又平面BDE，平面BDE，‎ ‎ 所以CG∥平面BDE． ……6分 ‎  （2）取AB中点P，连结FP，CP，‎ ‎ 因为F是BE的中点，‎ ‎ 所以FP∥AE，且.‎ ‎ 因为EA和DC都垂直于平面ABC，‎ ‎ 所以CD∥AE. ‎ ‎ 又AE=2CD，所以CD∥PF，且CD=PF，‎ ‎ 所以四边形CDFP是平行四边形.‎ ‎ 所以CP∥DF. ……8分 ‎ 因为AC＝BC，P为AB中点，‎ ‎ 所以CP⊥AB，所以DF⊥AB.‎ ‎ 因为EA垂直于平面ABC，平面ABC，‎ ‎ 所以CP⊥AE，所以DF⊥AE. ……10分 ‎ 因为，平面ABE，‎ ‎ 所以DF⊥平面ABE. 因为平面ABE，‎ ‎ 所以DF⊥AF. ……12分 ‎ 因为AB=AE，F是BE的中点，‎ ‎ 所以AF⊥BE.‎ ‎ 因为，平面BDE，‎ ‎ 所以AF⊥平面BDE. ……14分 ‎17．（本小题满分14分）‎ 解：（1）以点A为原点，AB所在直线为x轴建立平面直角坐标系，‎ ‎ 则，，，‎ ‎ 所以直线PQ的方程为，‎ ‎ 即. ……3分 ‎ 因为直线PQ与圆O相切，‎ ‎ 所以圆心到直线PQ的距离为，‎ ‎ 化简得， ……5分 ‎ 解得，‎ ‎，. ……7分 ‎ （2）因为，‎ ‎ 则，……9分 因为，所以，‎ 所以 令，得， ……11分 则时，，单调递减，‎ 时，，单调递增，‎ ‎ 所以时，取得最小值为百米. ‎ ‎ 答：设计成时，可使观赏道PQ的长l最短. ……14分 ‎18．（本小题满分16分）‎ ‎【解】（1）设椭圆的焦距为2c，‎ 由题意，得 ‎ 解得所以椭圆的方程为． ……3分 ‎ ‎（2）由题意，设直线l的方程为，‎ 联立方程组得 ，‎ 因为直线l与椭圆有且只有一个公共点，‎ 所以 解得 ，‎ 所以直线l的方程为． ……6分 ‎（3）当直线l的斜率不存在时，l与直线无交点，不符合题意，‎ 故直线l的斜率一定存在，设其方程为y=kx+m，‎ 由得，‎ ‎ 因为直线l与椭圆有且只有一个公共点，‎ ‎ 所以，‎ 化简得：， ……8分 ‎ 所以，即，‎ 因为直线l与直线相交于，所以，……10分 设， ‎ 所以，‎ 即对任意的k,m恒成立， ……14分 所以，即，‎ 所以点坐标为. ……16分 ‎19．（本小题满分16分）‎ 解：（1）因为，‎ ‎ 所以时，，即.‎ ‎ 因为时，，‎ 即.‎ n=1时也适合该式.‎ 所以时，，‎ ‎，‎ 两式相减得，‎ 则，‎ 两式相减得.‎ 所以，‎ 所以.‎ 所以数列{an}为等差数列. ‎ 因为，，所以公差，‎ 所以. ……4分 ‎（2）①因为an =n，‎ 所以 ‎  ， ……6分 所以，…8分 ‎ ②要证，只要证，‎ ‎ 只要证，即证.…10分 ‎ 设，x>1，令，‎ ‎ 则， ……12分 易证，故在上恒成立.‎ ‎ 所以在上单调递增，‎ ‎ 因为，所以.‎ ‎ 所以所证不等式成立. ……16分 ‎20．（本小题满分16分）‎ ‎【解】（1）因为函数在上单调递减，‎ 所以解得.‎ 因为在上单调递减，‎ 所以在上恒成立，‎ 即在上恒成立，‎ 所以在上恒成立. ……2分 ‎ 令，则，令，得，‎ ‎ 当时，，单调递增；‎ ‎    当时，，单调递减，‎ ‎ 所以，所以.‎ ‎ 故实数a的取值范围为. ……4分 ‎  （2）因为，所以.‎ ‎ 当时，， ‎ 所以恒成立，‎ 所以在（0，+∞）上单调递增.‎ ‎ 因为，‎ 所以，使得.，即.‎ 所以当时，，单调递减；‎ 当时，，单调递增.‎ 从而. ……8分 令，则.‎ 所以在单调递减，‎ 因此，.‎ 所以. ……10分 ‎（3） 因为，，‎ ‎ 所以，‎ ‎ 即.‎ ‎  所以，‎ ‎ 当时，在上恒成立，则h(x)在上单调递减，‎ ‎  故h(x)不可能有两个不同的零点. ……12分 ‎  当时，，令，‎ ‎   则函数与函数零点相同.‎ ‎   因为，令，‎ ‎   则在上恒成立，因为，则 x ‎1‎ ‎-‎ ‎0‎ ‎+‎ 递减 极小值 递增 所以的极小值为，‎ 所以要使由两个不同零点，则必须，‎ 所以a的取值范围为. ……14分 因为，，又在内连续且单调，‎ 所以在内有唯一零点.‎ 又，且，‎ 又在内连续且单调，所以在内有唯一零点.‎ 所以满足条件的a的取值范围为. ……16分 ‎21．【选做题】‎ A．[选修4-2：矩阵与变换]（本小题满分10分）‎ ‎【解】（1）因为是矩阵的特征值所对应的一个特征向量，‎ ‎ 所以，即，‎ ‎ 所以解得 ‎ 所以矩阵 ……4分 ‎ （2）设曲线上任一点在矩阵的作用下得到曲线上一点，‎ 则，‎ ‎ 所以解得 ‎ 因为，‎ ‎ 所以，即曲线的方程为． ……10分 B．[选修4-4：坐标系与参数方程]（本小题满分10分）‎ ‎【解】曲线的直角坐标方程为， ……3分 即，圆心，半径，‎ ‎ 直线l的普通方程为， ……6分 ‎ 所以圆心到直线l的距离，‎ ‎ 所以直线l被曲线截得的线段长度……10分 C．[选修4-5：不等式选讲]（本小题满分10分）‎ 已知x，y，z是正实数，且，求证：．‎ 证明：由柯西不等式得 …… 6分 ‎ 因为， 所以， ‎ 所以，当且仅当时取等号．……………… 10分 ‎【必做题】第22、23题，每小题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎22．(本小题满分10分)‎ 解:（1）设T的坐标为，则B为，‎ 因为 A（0，1），所以，‎ 因为，所以，‎ 所以，所以，‎ 即 ，所以曲线C的方程为 ……4分 ‎（2）法一：由题意，直线的斜率必存在，设为 则直线的方程为：， ‎ x y P N1‎ M N M1‎ O 由可得：‎ 设，‎ 则 ‎①因为，所以 因为 所以，所以 解得： ……6分 ‎②因为点关于y轴的对称点为，所以 所以 所以直线的方程为：‎ 令得：‎ 所以直线过定点，定点坐标为 ……10分 ‎（2）法二：设， ‎ ‎ 因为三点共线，所以，‎ 所以，化简得：‎ 因为，所以 ‎①由题意：，所以 因为，所以，所以，‎ 所以，所以，解得： ……6分 ‎②因为点关于y轴的对称点为，所以 所以，‎ 所以直线的方程为：‎ 令得：‎ 所以直线过定点，定点坐标为 ……10分 ‎23．(本小题满分10分)‎ ‎ 【解析】（1）证明：‎ ‎． ……3分 ‎ ‎（2）用数学归纳法证明．‎ ① 当时，左边=右边；‎ 当时，由（1）得左边=右边；‎ ② 设当时，结论成立，即有， ……5分 则当时，‎ 由（1）得，‎ 所以， ……8分 所以 所以时结论成立．‎ 由①②可知原不等式成立． ……10分