【数学】2019届一轮复习北师大版空间几何体学案

【数学】2019届一轮复习北师大版空间几何体学案

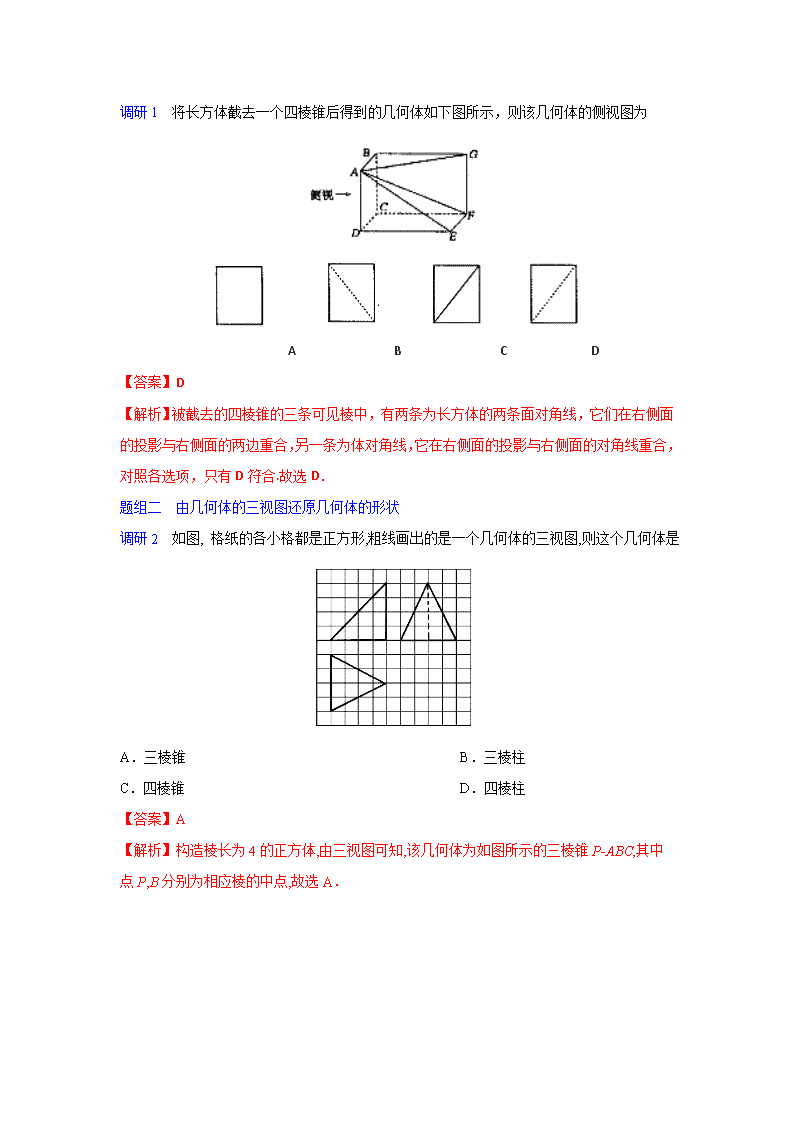
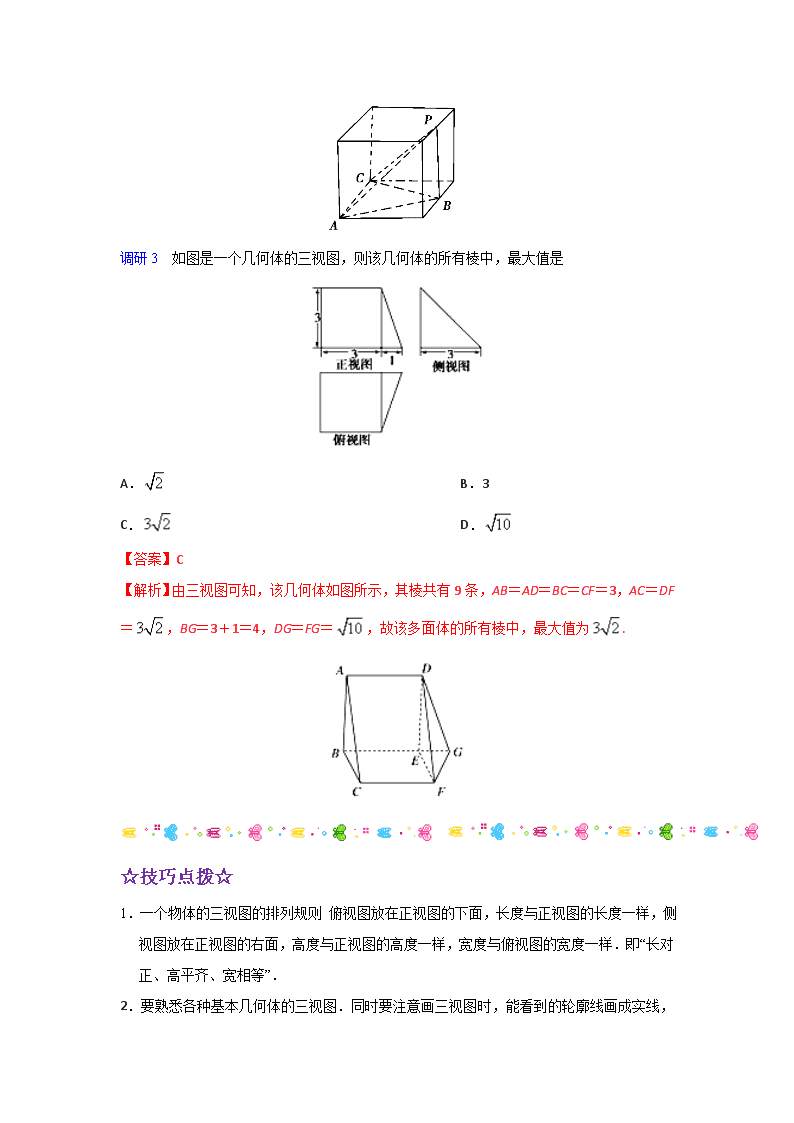
‎ ‎ 高考考点 命题分析 三年高考探 ‎ 考查频率 空间几何体与 三视图 立体几何问题既是高考的必考点，也是考查的难点，其在高考中的命题形式较为稳定，保持“一小一大”或“两小一大”的格局．多以选择题或者填空题的形式考查空间几何体三视图的识别，空间几何体的体积或表面积的计算. ]‎ ‎2017课标全国Ⅰ7‎ ‎2016课标全国Ⅱ6 ‎ ‎★★★★★ [ ]‎ 空间几何体的[ 。 。 ]‎ 表面积与体积 ‎2017课标全国Ⅱ4‎ ‎2015课标全国Ⅰ6‎ ‎★★★★★‎ 空间几何体与球的切、接问题 ‎2017课标全国Ⅲ8‎ ‎★★★‎ 考点1 空间几何体与三视图 题组一 画空间几何体的三视图 调研1 将长方体截去一个四棱锥后得到的几何体如下图所示，则该几何体的侧视图为 ‎ ‎ A B C D ‎【答案】D ‎【解析】被截去的四棱锥的三条可见棱中，有两条为长方体的两条面对角线，它们在右侧面的投影与右侧面的两边重合，另一条为体对角线，它在右侧面的投影与右侧面的对角线重合，对照各选项，只有D符合.故选D． ‎ 题组二 由几何体的三视图还原几何体的形状 调研2 如图, 格纸的各小格都是正方形,粗线画出的是一个几何体的三视图,则这个几何体是 A．三棱锥　　　 B．三棱柱 C．四棱锥　　　 D．四棱柱 ‎【答案】A ‎【解析】构造棱长为4的正方体,由三视图可知,该几何体为如图所示的三棱锥P-ABC,其中点P,B分别为相应棱的中点,故选A．‎ 调研3 如图是一个几何体的三视图，则该几何体的所有棱中，最大值是 A． B．3‎ C． D．‎ ‎【答案】C ‎【解析】由三视图可知，该几何体如图所示，其棱共有9条，AB＝AD＝BC＝CF＝3，AC＝DF＝，BG＝3＋1＝4，DG＝FG＝，故该多面体的所有棱中，最大值为. ‎ ‎☆技巧点拨☆‎ ‎1．一个物体的三视图的排列规则 俯视图放在正视图的下面，长度与正视图的长度一样，侧视图放在正视图的右面，高度与正视图的高度一样，宽度与俯视图的宽度一样．即“长对正、高平齐、宽相等”．‎ ‎2．‎ 要熟悉各种基本几何体的三视图．同时要注意画三视图时，能看到的轮廓线画成实线，看不到的轮廓线画成虚线．‎ 题组三 由几何体的部分视图画出剩余部分的视图 调研4 一个三棱锥的正视图和俯视图如图所示，则该三棱锥的侧视图可能为 ‎ ‎ ‎【答案】D ‎【解析】由几何体的正视图和俯视图可知，三棱锥的顶点在底面内的射影在底面棱上，则原几何体如图所示，从而侧视图为D．故选D． ‎ 考点2 空间几何体的表面积与体积 题组一 柱体、锥体、台体的表面积与体积 调研1 一个几何体的三视图如图所示，则这个几何体的体积为 A． B．‎ C． D．‎ ‎【答案】D ‎【解析】由三视图可知几何体是由一个四棱锥和半个圆柱组合而成的，所以所求的体积为，故选D. ‎ 调研2 在四棱锥中，底面是边长为2的菱形， ，侧棱底面， ，为的中点，则四面体的体积为__________．‎ ‎【答案】‎ ‎【解析】侧棱底面，是四面体的高，底面是边长为的菱形， ，，为的中点，三角形的面积，四面体的体积等于四面体的体积，为，故答案为.‎ 调研3如图，三棱柱中，侧面侧面，， ．‎ ‎（1）求证 ；‎ ‎（2）求三棱柱的侧面积．‎ ‎【解析】（1）如图，取的中点，连接，，，‎ ‎∵，，∴为正三角形，∴，，‎ 又侧面侧面，平面平面，平面，∴平面，‎ 又平面，∴，‎ 在中，∵，，，∴，解得， ‎ ‎∴，∴，‎ 又，平面，平面，∴平面，‎ ‎∵平面，∴．‎ ‎（2）依题意，，‎ 如图，在平行四边形中，过点作于点，‎ 过点作于点，连接，则为矩形，∴，‎ 由（1）知平面，平面，∴，‎ ‎∵，，平面，平面，∴平面，‎ ‎∵平面，∴，‎ ‎，‎ 在中，，，∴，‎ ‎∴，又，‎ ‎∴三棱柱的侧面积． ‎ ‎☆技巧点拨☆‎ 求解几何体的表面积或体积的方法 ‎ ‎(1)对于规则几何体，可直接利用公式计算．‎ ‎(2)对于不规则几何体，可采用割补法求解.对于某些三棱锥，有时可采用等体积转换法求解．‎ ‎(3)求解旋转体的表面积和体积时，注意圆柱的轴截面是矩形，圆锥的轴截面是等腰三角形，圆台的轴截面是等腰梯形的应用．‎ 题组二 球的表面积和体积 调研4 某几何体的三视图如图所示,其中俯视图是半圆里面内切一个小圆,若该几何体的表面积为,则正视图中的值为 A．1 B．2‎ C．3 D．4‎ ‎【答案】B ‎【解析】由三视图可知，该几何体是 上面是一个直径为a的球，下面是一个底面半径为2、高为4的圆柱的一半，则，所以a=2. ‎ 调研5 若球的体积为4π，平面α截球O的球面所得圆的半径为1，则球心O到平面α的距离为 A．1 B．‎ C． D．‎ ‎【答案】B ‎【解析】依题意，设该球的半径为R，则有R3＝4π，由此解得R＝，因此球心O到平面α的距离d＝.选B.‎ ‎☆技巧点拨☆‎ 有关球的截面问题，常画出截面圆，将空间几何问题转化为平面中圆的有关问题解决.球心到截面的距离与球的半径及截面圆的半径之间满足关系式 .‎ 考点3 空间几何体与球的切、接问题 题组一 与球切、接求表面积与体积问题 调研1 已知S，A，B，C是球O表面上的不同点，SA⊥平面ABC，AB⊥BC，AB＝1，BC＝.若球O的表面积为4π，则SA＝‎ A． B．1‎ C． D． ‎【答案】B ‎【解析】根据已知把补成如图所示的长方体．因为球O的表面积为4π，所以球O的半径R＝1,2R＝＝2，解得SA＝1，故选B．‎ 调研2 已知是某球面上不共面的四点，且，， ，则此球的体积为 A． B．‎ C． D．‎ ‎【答案】A ‎【解析】由，得，又，所以平面，则，又,所以都是直角三角形，由三棱锥的外接球的性质知，球心为的中点，且球的半径，所以球的体积，选A． ‎ ‎☆技巧点拨☆‎ ‎1．解决与球有关的“切”“接”问题，一般要过球心及多面体中的特殊点或过线作截面，把空间问题转化为平面问题，从而寻找几何体各元素之间的关系．‎ ‎2．构造法在定几何体外接球球心中的应用 常见的构造条件及构造方法有 ‎ ‎(1)正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥，可将三棱锥补形成长方体或正方体；‎ ‎(2)同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥，可将三棱锥补形成长方体或正方体；‎ ‎(3)若已知棱锥含有线面垂直关系，则可将棱锥补形成长方体或正方体；‎ ‎(4)若三棱锥的三个侧面两两垂直，则可将三棱锥补形成长方体或正方体．‎ ‎3．性质法在定几何体外接球球心中的应用 立体几何问题转化为平面几何问题，体现了等价转化思想与数形结合思想，方法是利用球心O与截面圆圆心O′的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质，确定球心．‎ ‎4．记住几个常用的结论 ‎ ‎(1)正方体的棱长为a，球的半径为R.‎ ‎①对于正方体的外接球，2R＝a；‎ ‎②对于正方体的内切球，2R＝a；‎ ‎③对于球与正方体的各棱相切，2R＝a．‎ ‎(2)在长方体的同一顶点的三条棱长分别为a，b，c，球的半径为R，则2R＝.‎ ‎(3)正四面体的外接球与内切球的半径之比为3∶1.‎ 题组二 与球切、接有关的几何体的最值问题 调研3 表面积为16π的球内接一个正三棱柱,则此三棱柱体积的最大值为 A．4 B．‎ C．8 D．‎ ‎【答案】C ‎ ‎【解析】由题意,得该球的半径为2,设正三棱柱的侧棱长为,底面边长为,则,=，即，则该正三棱柱的体积为，则，当时，；当时，，即当时，取到极大值,也是最大值，为8,故所求三棱柱的体积的最大值为8.故选C．‎ 调研4 已知正四棱柱的底面边长为，高为，其所有顶点都在球的球面上，若该正四棱柱的侧面积为4，则球的表面积的最小值为__________．‎ ‎【答案】‎ ‎【解析】正四棱柱的侧面积为，体对角线长为外接球O的直径，所以，所以，则球的表面积为，所以球的表面积的最小值为. ‎ ‎☆技巧点拨☆‎ 与球切、接有关的几何体的最值问题多涉及体积最值问题、截面面积最值问题．求解此类问题的关键是结合图形分析取得最值的条件转化求解，有时也可建立目标函数转化为函数最值求解．‎ ‎1．（广东省佛山市顺德区2018届高三下 期 情调研考试）一个几何体的三视图如图所示，那么该几何体的表面积是 A． B．‎ C． D．‎ ‎【答案】B ‎ ‎ ‎ ‎2．（2017-2018 年湖北省鄂南高中、华师一附中、黄冈中 等八校高三第一次联考）将正方体(如图1)截去三个三棱锥后,得到如图2所示的几何体,侧视图的视线方向如图2所示,则该几何体的侧视图为 ‎ ‎ A B C D ‎【答案】D ‎【解析】由该几何体的直观图可知，答案为D． ‎ ‎3．（安徽省滁州市2018届高三上 期期末考试）‎ 榫卯是中国古代建筑、家具及其他器械的主要结构方式，是在两个构件上采用凹凸部位相结合的一种连接方式，凸出部分叫做“榫头”.若某“榫头”的三视图如图所示，则该“榫头”的体积为 A． B．‎ C． D．‎ ‎【答案】C ‎4．（河南省濮阳市2018届高三第一次模拟考试）如图，为棱长为的正方体的上、下底面的中心，若正方体以为轴顺时针旋转，则该正方体的所有正视图中最大面积是 A． B．‎ C． D．‎ ‎【答案】B ‎【解析】所有正视图中最大面积是长为，宽为的矩形，面积为，选B．‎ ‎5．（2017-2018 年广东省珠海市珠海二中、斗门一中高三上 期期中联考）多面体 的底面为矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则的长为 A． B．‎ C． D．‎ ‎【答案】C ‎ ‎ ‎6．（2017-2018 年河南省郑州市第一中 高三上 期第二次月考）如下左图所示为一个正三棱柱被平面截得的几何体,其中,几何体的俯视图如下右图所示,则该几何体的正视图是 A． B．‎ C． D．‎ ‎【答案】A ‎【解析】由直观图和俯视图可知底面是正三角形,则正视图中点的射影是的中点,棱的射影与平行，即正视图是选项A．‎ ‎7．(2017安徽六校素质测试) 如图， 格纸上每个小正方形的边长为1，图中粗线画出的是某多面体的三视图，则该几何体的表面中互相垂直的平面有 A．3对 B．4对 C．5对 D．6对 ‎【答案】B ‎8．（安徽省池州市 2017-2018 年高三上 期期末）中国古代第一部数 名著《九章算术》中，将一般多面体分为阳马、鳖臑、堑堵三种基本立体图形，其中将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥为鳖臑，平面， ， ， ，则三棱锥外接球的表面积为 A． B．‎ C． D．‎ ‎【答案】D ‎9．（贵州省凯里市第一中 2018届高三下 期考试）已知某几何体是两个正四棱锥的组合体，其三视图如下图所示，则该几何体外接球的表面积为 A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】由已知三视图得该几何体的直观图如下 ‎ 可知该几何体外接球的半径为，则该几何体外接球的表面积为，故选D.‎ ‎10．（内蒙古集宁一中2018届高三上 期期末考试）一个三棱锥内接于球，且，，，则球心到平面的距离是 A． B．‎ C． D．‎ ‎【答案】D ‎ ‎ ‎11．（江苏省淮安市等四市2018届高三上 期第一次模拟）已知正四棱柱的底面边长为，侧面的对角线长是，则这个正四棱柱的体积是____．‎ ‎【答案】‎ ‎【解析】易知正四棱柱的高为cm，‎ 所以正四棱柱的体积是.‎ ‎12．(2017广西三市联考)已知长方体ABCD-A1B‎1C1D1内接于球O, 底面ABCD是边长为2的正方形，E为AA1的中点，OA⊥平面BDE，则球O的表面积为________．‎ ‎【答案】16π ‎ ‎ ‎13．（2017-2018 年云南省师范大 附属中 高三12月高考适应性月考）已知半径为5的球被两平行的平面所截,两截面圆的半径分别为3和4,则分别以两截面为上、下底面的圆台的侧面积为________．‎ ‎【答案】或 ‎【解析】由题意,得两截面圆到球心的距离分别为,则分别以两截面为上、下底面的圆台的底面半径分别为4,3,‎ 圆台的高为或,则其母线长为或,‎ 则该圆台的侧面积为或．‎ ‎14．（2017-2018 年内蒙古集宁一中高三上 期第二次月考）在正方体ABCD﹣A1B1C1D1中,若棱长AB=3,则点B1到平面ACD1的距离为 　　　　　　  .‎ ‎【答案】‎ ‎【解析】易知四面体B1ACD1是棱长为的正四面体，△ACD1的面积为易得四面体B1ACD1的体积为,设点B1到平面ACD1的距离为h,则.‎ ‎15．（衡水金卷2018年普通高等 校招生全国统一考试模拟试卷）一底面为正方形的长方体各棱长之和为24，则当该长方体体积最大时，其外接球的体积为__________．‎ ‎【答案】‎ ‎16．（河南省濮阳市2018届高三第一次模拟考试）如图，正方形中，，与交于点，现将沿折起得到三棱锥，，分别是，的中点.‎ ‎(1)求证 ；‎ ‎(2)若三棱锥的最大体积为，当三棱锥的体积为，且为锐角时，求三棱锥的体积.‎ ‎ ‎ ‎17．（广西桂林市、贺州市2018届高三上 期期末联考）如图，为底面边长为2，高为的正三棱柱，经过的截面与上底面相交于，设.‎ ‎（1）证明 ；‎ ‎（2）当时，在图中作出点在平面内的正投影（说明作法及理由），并求四棱锥的表面积.‎ ‎【解析】（1）∵平面平面，平面平面，平面 平面，∴，‎ 又∵，∴.‎ ‎ ‎ ‎1． (2017新课标全国Ⅰ理 )某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为 A．10 B．12‎ C．14 D．16‎ ‎【答案】B ‎2．（2017新课标全国Ⅲ理 ）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为 A． B． ‎ C． D．‎ ‎【答案】B ‎【解析】绘制圆柱的轴截面如图所示 ‎ 由题意可得 ，‎ 结合勾股定理，底面半径，‎ 由圆柱的体积公式，可得圆柱的体积是，故选B．‎ ‎【名师点睛】（1）求解空间几何体体积的关键是确定几何体的元素以及线面的位置关系和数量关系，利用相应体积公式求解；（2）若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解.‎ ‎3．(2016新课标全国II理 )如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为 A．20 B．24‎ C．28 D．32‎ ‎【答案】C ‎4．(2015新课标全国I理 )《九章算术》是我国古代内容极为丰富的数 名著，书中有如下问题 “今有委米依垣内角，下周八尺，高五尺.问 积及为米几何?”其意思为 “在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有 A．14斛 B．22斛 C．36斛 D．66斛 ‎【答案】B ‎【解析】设圆锥底面半径为r，则 ，所以米堆的体积为 故堆放的米约为斛，故选B．‎ ‎【名师点睛】本题以《九章算术》中的问题为材料，试题背景新颖，解答本题的关键应想到米堆是圆锥，底面周长是两个底面半径与圆的和，根据题中的条件列出关于底面半径的方程，解出底面半径，是基础题.‎ ‎5．(2015新课标全国II理 )已知A,B是球O的球面上两点，∠AOB=90°,C为该球面上的动点，若三棱锥体积的最大值为36，则球O的表面积为 A．36π B．64π C．144π D．256π ‎【答案】C ‎ ‎