- 2021-06-11 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学选修2-1公开课课件3_1_5空间向量运算的坐标表示
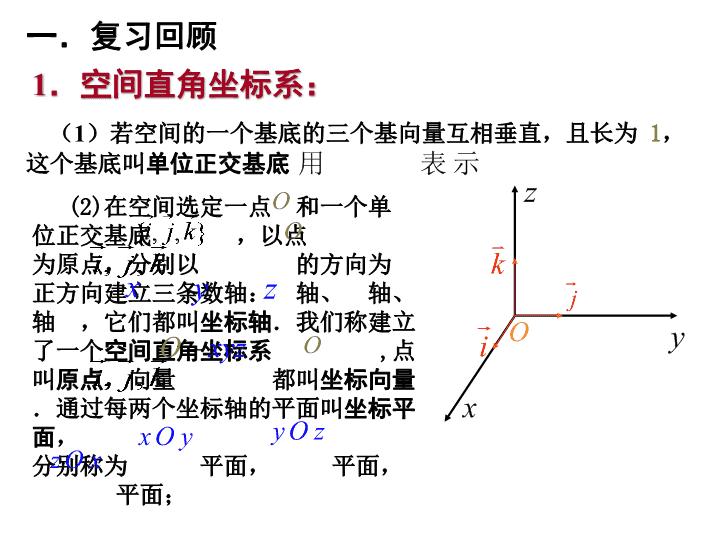
3.1.5 空间向量运算的 坐标表示 1 .空间向量的基本定理: 2 .平面向量的坐标表示及运算律: 一.复习回顾 若是 空间的一个基底, 是空间任意一向量,存在唯一的实数组使. 1 .空间直角坐标系: ( 1 )若空间的一个基底的三个基向量互相垂直,且长为 1 , 这个基底叫 单位正交基底 (2) 在空间选定一点 和一个单位正交基底 ,以点 为原点,分别以 的方向为正方向建立三条数轴: 轴、 轴、 轴 ,它们都叫 坐标轴 .我们称建立了一个 空间直角坐标系 , 点 叫 原点 ,向量 都叫 坐标向量 .通过每两个坐标轴的平面叫 坐标平面 , 分别称为 平面, 平面, 平面; 一.复习回顾 ( 4 )在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向 轴的正方向,如果中指指向 轴的正方向,称这个坐标系为 右手直角坐标系 。本书建立的坐标系都是右手直角坐标系 . ( 3 )作空间直角坐标系 时,一般使 2 .空间直角坐标系中的坐标: 如图给定空间直角坐标系和向量 ,设 为坐标向量 , 则存在唯一的有序实数组 ,使 , 有序实数组 叫作向量 在空间直角坐标系 中的坐标,记作 . 在空间直角坐标系 中,对空间任一点 ,存在唯一的有序实数组 ,使 ,有序实数组 叫作向量 在 空间直角坐标系 中的 坐标 , 记作 , 叫 横坐标 , 叫 纵坐标 , 叫 竖坐标 . 一、向量的直角坐标运算 新课 1. 距离公式 ( 1 )向量的长度(模)公式 注意:此公式的几何意义是表示长方体的对角线的长度。 二、距离与夹角 在空间直角坐标系中,已知 、 ,则 ( 2 )空间两点间的距离公式 2. 两个向量夹角公式 注意: ( 1 )当 时, 同向; ( 2 )当 时, 反向; ( 3 )当 时, 。 思考:当 及 时,夹角在什么范围内? 例 1 .已知 解 : 三、应用举例 三、应用举例 例 2 已知 、 ,求: ( 1 )线段 的中点坐标和长度; 解:设 是 的中点,则 ∴ 点 的坐标是 . ( 2 )到 两点距离相等的点 的 坐标 满足的条件。 解:点 到 的距离相等,则 化简整理,得 即到 两点距离相等的点的坐标 满 足的条件是 解:设正方体的棱长为 1 ,如图建 立空间直角坐标系 ,则 例 3 如图 , 在正方体 中, ,求 与 所成的角的余弦值 . 证明:不妨设已知正方体的棱长为 1 个单 位长度 , 设 分别以 为坐标向量建立空间直 角坐标系 则 例 4 . 在正方体 练习 3 已知 垂直于正方形 所在的平面 , 分别是 的中点 , 并且 , 求证 : 证明 : 分别以 为坐标向量建立空间直角坐标系 则 练习 4 :如图,已知线段 AB⊂ α , AC ⊥α , BD ⊥ AB , DE ⊥α ,∠ DBE=30 º ,如果 AB=6 , AC=BD=8 ,求 CD 的长及异面直线 CD 与 AB 所成角的大小。 练习:平行六面体 ABCD—A 1 B 1 C 1 D 1 中, AB=4 , AD=3 , AA 1 =5 ,∠ BAD=∠BAA 1 =∠DAA 1 =60 º , E 、 H 、 F 分别是 D 1 C 1 、 AB 、 CC 1 的中点。( 1 )求 AC 1 的长;( 2 )求 BE 的长;( 3 )求 HF 的长;( 4 )求 BE 与 HF 所成角的大小。 10 证明 : 设正方体的棱长为 1, 建立如图的空间直角坐标系 x y z A 1 D 1 C 1 B 1 A C B D F E查看更多