2021届高考数学一轮复习第二章函数概念及基本初等函数Ⅰ第8节函数与方程课件新人教A版

2021届高考数学一轮复习第二章函数概念及基本初等函数Ⅰ第8节函数与方程课件新人教A版

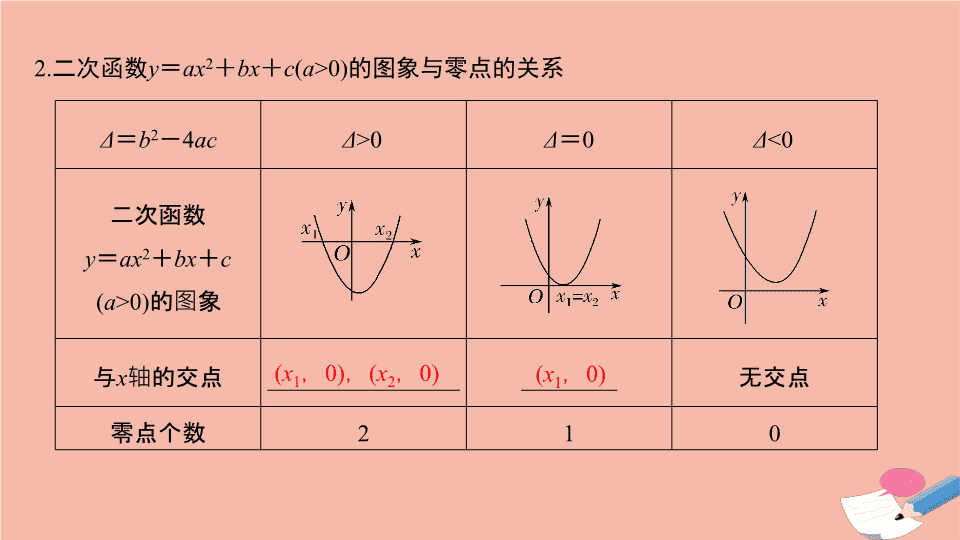
第 8 节　函数与方程 考试要求　 结合二次函数的图象，了解函数的零点与方程根的联系，判断一元二次方程根的存在性及根的个数 . 知 识 梳 理 1. 函数的零点 (1) 函数零点的概念 对于函数 y ＝ f ( x ) ，把使 __________ 的实数 x 叫做函数 y ＝ f ( x ) 的零点 . (2) 函数零点与方程根的关系 方程 f ( x ) ＝ 0 有实数根 ⇔ 函数 y ＝ f ( x ) 的图象与 ______ 有交点 ⇔ 函数 y ＝ f ( x ) 有 ______ . (3) 零点存在性定理 如果函数 y ＝ f ( x ) 满足： ① 在区间 [ a ， b ] 上的图象是连续不断的一条曲线； ② ____________ ；则函数 y ＝ f ( x ) 在 ( a ， b ) 内有零点，即存在 c ∈ ( a ， b ) ，使得 f ( c ) ＝ 0 ，这个 c 也就是方程 f ( x ) ＝ 0 的根 . f ( x ) ＝ 0 x 轴 零点 f ( a )· f ( b )<0 2. 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a >0) 的图象与零点的关系 Δ ＝ b 2 － 4 ac Δ >0 Δ ＝ 0 Δ <0 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a >0) 的图象 与 x 轴的交点 ________________ ________ 无交点 零点个数 2 1 0 ( x 1 ， 0) ， ( x 2 ， 0) ( x 1 ， 0) [ 常用结论与微点提醒 ] 1. 若连续不断的函数 f ( x ) 在定义域上是单调函数，则 f ( x ) 至多有一个零点 . 函数的零点不是一个 “ 点 ” ，而是方程 f ( x ) ＝ 0 的实根 . 2. 由函数 y ＝ f ( x )( 图象是连续不断的 ) 在闭区间 [ a ， b ] 上有零点不一定能推出 f ( a )· f ( b )<0 ，如图所示，所以 f ( a )· f ( b )<0 是 y ＝ f ( x ) 在闭区间 [ a ， b ] 上有零点的充分不必要条件 . 3. 周期函数如果有零点，则必有无穷多个零点 . 诊 断 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) (1) 函数 f ( x ) ＝ lg x 的零点是 (1 ， 0).( 　　 ) (2) 图象连续的函数 y ＝ f ( x )( x ∈ D ) 在区间 ( a ， b ) ⊆ D 内有零点，则 f ( a )· f ( b )<0.( 　　 ) (3) 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠ 0) 在 b 2 － 4 ac <0 时没有零点 .( 　　 ) 解析 　 (1) f ( x ) ＝ lg x 的零点是 1 ，故 (1) 错 . (2) f ( a )· f ( b ) ＜ 0 是连续函数 y ＝ f ( x ) 在 ( a ， b ) 内有零点的充分不必要条件，故 (2) 错 . 答案 　 (1) × 　 (2) × 　 (3) √ 2. ( 老教材必修 1P92A2 改编 ) 已知函数 f ( x ) 的图象是连续不断的，且有如下对应值表： 在下列区间中，函数 f ( x ) 必有零点的区间为 ( 　　 ) A.(1 ， 2) B.(2 ， 3) C.(3 ， 4) D.(4 ， 5) 解析 　由所给的函数值的表格可以看出， x ＝ 2 与 x ＝ 3 这两个数字对应的函数值的符号不同，即 f (2)· f (3)<0 ，所以函数在 (2 ， 3) 内有零点 . 答案 　 B x 1 2 3 4 5 f ( x ) － 4 － 2 1 4 7 3. ( 新教材必修第一册 P143 例 1 改编 ) 函数 f ( x ) ＝ e x ＋ 3 x 的零点个数是 ( 　　 ) A.0 B.1 C.2 D.3 4. (2020· 石家庄模拟 ) f ( x ) ＝ e x － x － 2 在下列哪个区间必有零点 ( 　　 ) A.( － 1 ， 0) B.(0 ， 1) C.(1 ， 2) D.(2 ， 3) 5. (2019· 全国 Ⅲ 卷 ) 函数 f ( x ) ＝ 2sin x － sin 2 x 在 [0 ， 2π] 的零点个数为 ( 　　 ) A.2 B.3 C.4 D.5 解析　 2sin x － sin 2 x ＝ 0 ，得 sin x ＝ 0 或 cos x ＝ 1. 又 x ∈ [0 ， 2π] ，由 sin x ＝ 0 ，得 x ＝ 0 ， π ， 2π. 由 cos x ＝ 1 ，得 x ＝ 0 ， 2π. ∴ f ( x ) ＝ 0 有三个实根 0 ， π ， 2π ，即 f ( x ) 在 [0 ， 2π] 上有三个零点 . 答案　 B 6. (2020· 济南质检 ) 若二次函数 f ( x ) ＝ x 2 － 2 x ＋ m 在区间 (0 ， 4) 上存在零点，则实数 m 的取值范围是 ________. 解析　 m ＝－ x 2 ＋ 2 x 在 (0 ， 4) 上有解， 又－ x 2 ＋ 2 x ＝－ ( x － 1) 2 ＋ 1 ， ∴ y ＝－ x 2 ＋ 2 x 在 (0 ， 4) 上的值域为 ( － 8 ， 1] ， ∴ － 8< m ≤ 1. 答案　 ( － 8 ， 1] 考点一　函数零点所在区间的判定 所以 g (2)· g (3)<0. 故函数 g ( x ) 的零点所在区间为 (2 ， 3). 所以 f (1)· f (2)<0 ，所以 x 0 ∈ (1 ， 2). 答案　 (1)C 　 (2)(1 ， 2) 规律方法　 1. 确定函数 f ( x ) 的零点所在区间的常用方法： (1) 利用函数零点的存在性定理：首先看函数 y ＝ f ( x ) 在区间 [ a ， b ] 上的图象是否连续，再看是否有 f ( a )· f ( b )<0. 若有，则函数 y ＝ f ( x ) 在区间 ( a ， b ) 内必有零点 . (2) 数形结合法：通过画函数图象，观察图象与 x 轴在给定区间上是否有交点来判断 . 2. 函数的零点存在性定理只能判断函数在某个区间上的变号零点，不满足条件时，一定要综合函数性质进行分析判断 . A.(0 ， 1) B.(1 ， 2) C.(2 ， 3) D.(3 ， 4) 又 f (1) ＝ 1 － 2<0 ， f (2) ＝ 2 － 1>0 ， ∴ f (1)· f (2)<0. 故函数 f ( x ) 的零点所在的区间为 (1 ， 2). 答案　 B 考点二　确定函数零点的个数 A.0 B.1 C.2 D.3 (2) (2020· 惠州质检 ) 函数 f ( x ) ＝ | x － 2| － ln x 在定义域内的零点的个数为 ( 　　 ) A.0 B.1 C.2 D.3 解析　 (1) 当 x >1 时，令 f ( x ) ＝ ln( x － 1) ＝ 0 ，得 x ＝ 2. 当 x ≤ 1 时，令 f ( x ) ＝ 2 x － 1 － 1 ＝ 0 ，得 x ＝ 1. ∴ 函数 f ( x ) 的零点为 x ＝ 1 与 x ＝ 2 ，有 2 个零点 . (2) 由题意可知 f ( x ) 的定义域为 (0 ，＋ ∞ ) ，在同一直角坐标系中画出函数 y ＝ | x － 2|( x >0) ， y ＝ ln x ( x >0) 的图象，如图所示 . 由图可知函数 f ( x ) 在定义域内的零点个数为 2. 答案　 (1)C 　 (2)C 规律方法　 函数零点个数的判断方法： (1) 直接求零点，令 f ( x ) ＝ 0 ，有几个解就有几个零点； (2) 零点存在性定理，要求函数在区间 [ a ， b ] 上是连续不断的曲线，且 f ( a )· f ( b )<0 ，再结合函数的图象与性质确定函数零点个数； (3) 利用图象交点个数，作出两函数图象，观察其交点个数即得零点个数 . 法二　 函数 f ( x ) 的图象如所示，由图象知函数 f ( x ) 共有 2 个零点 . 答案　 (1)B 　 (2)B 考点三　函数零点的应用　 多维探究 角度 1 　根据函数零点个数求参数 解析　 依题意直线 y ＝ a 与 y ＝ f ( x ) 的图象有两个交点 . 作出 y ＝ a ， y ＝ f ( x ) 的图象，如图所示 . 当 x >1 时， f ( x ) ＝－ x 2 ＋ 4 x － 2 ＝－ ( x － 2) 2 ＋ 2 ， ∴ 当 x ＝ 2 时， f ( x ) 有最大值 f (2) ＝ 2. 此时，方程 a ＝ f ( x ) 有两个不同实根 . 答案　 B 角度 2 　根据零点的范围求参数 【例 3 － 2 】 (1) 方程 2 x ＋ 3 x ＝ k 的解在 [1 ， 2) 内，则 k 的取值范围是 ________. (2) (2020· 合肥模拟 ) 已知 a ， b ， c ， d 都是常数， a > b ， c > d . 若 f ( x ) ＝ 2 020 ＋ ( x － a )( x － b ) 的零点为 c ， d ，则下列不等式正确的是 ( 　　 ) A. a > c > d > b B. a > b > c > d C. c > d > a > b D. c > a > b > d 解析　 (1) 令函数 f ( x ) ＝ 2 x ＋ 3 x － k ，则 f ( x ) 在 R 上是增函数 . 当方程 2 x ＋ 3 x ＝ k 的解在 (1 ， 2) 内时， f (1)· f (2)<0 ，即 (5 － k )(10 － k )<0 ，解得 5< k <10. 又当 f (1) ＝ 0 时， k ＝ 5. 综上，实数 k 的取值范围是 [5 ， 10). (2) 根据题意，设 g ( x ) ＝ ( x － a )( x － b ) ， 则 f ( x ) ＝ g ( x ) ＋ 2 020 ， 令 g ( x ) ＝ 0 ，则 x ＝ a 或 x ＝ b ， 则函数 g ( x ) 的图象与 x 轴的交点为 ( a ， 0) 和 ( b ， 0) ，如图 . 令 f ( x ) ＝ 2 020 ＋ ( x － a )( x － b ) ＝ 0 ，即 g ( x ) ＝－ 2 020 ， 因为 f ( x ) ＝ 2 020 ＋ ( x － a )( x － b ) 的零点为 c ， d ， 所以 g ( x ) 的图象与直线 y ＝－ 2 020 的交点为 ( c ，－ 2 020) 和 ( d ，－ 2 020) ，则有 a > c > d > b . 答案　 (1)[5 ， 10) 　 (2)A 规律方法　 1. 已知函数的零点求参数，主要方法有： (1) 直接求方程的根，构建方程 ( 不等式 ) 求参数； (2) 数形结合； (3) 分离参数，转化为求函数的最值 . 2. 已知函数零点的个数求参数范围，常利用数形结合法将其转化为两个函数的图象的交点问题，需准确画出两个函数的图象，利用图象写出满足条件的参数范围 . 【训练 3 】 (1) ( 角度 1)(2017· 全国 Ⅲ 卷 ) 已知函数 f ( x ) ＝ x 2 － 2 x ＋ a (e x － 1 ＋ e － x ＋ 1 ) 有唯一零点，则 a ＝ ( 　　 ) (2) ( 角度 2) 若函数 y ＝ x ＋ log 2 ( a － 2 x ) ＋ 2 在 R 上有零点，则实数 a 的最小值为 ________. 解析　 (1) f ( x ) ＝ ( x － 1) 2 － 1 ＋ a (e x － 1 ＋ e 1 － x ) ，则 f (2 － x ) ＝ (2 － x － 1) 2 － 1 ＋ a [e 2 － x － 1 ＋ e 1 － (2 － x ) ] ＝ (1 － x ) 2 － 1 ＋ a (e x － 1 ＋ e 1 － x ) ＝ f ( x ) ，即 f ( x ) 的图象关于直线 x ＝ 1 对称 . 或：作出 y ＝ a (e x － 1 ＋ e － x ＋ 1 ) 与 y ＝－ x 2 ＋ 2 x 的图象 . 结合函数的最值求解 ( 读者自行完成 ). (2) 令 x ＋ log 2 ( a － 2 x ) ＋ 2 ＝ 0 ，则 a － 2 x ＝ 2 － ( x ＋ 2). 依题意，关于 x 的方程 a ＝ 2 x ＋ 2 － ( x ＋ 2) 有解 . 当且仅当 x ＝－ 1 时，等号成立 . ∴ a ≥ 1 ，故 a 的最小值为 1. 答案　 (1)C 　 (2)1 直观想象 —— 解嵌套函数的零点问题 函数的零点是高考命题的热点，主要涉及判断函数零点的个数或范围，常考查三次函数与复合函数相关零点，与函数的性质和相关问题交汇 . 对于嵌套函数的零点，通常先 “ 换元解套 ” ，将复合函数拆解为两个相对简单的函数，借助函数的图象、性质求解 . 类型 1 　嵌套函数零点个数的判断 因此函数 y ＝ 2[ f ( x )] 2 － 3 f ( x ) ＋ 1 的零点有 5 个 . 答案 　 5 A.4 B.5 C.6 D.7 由图 ② ，结合图象，当 f ( x ) ＝ 0 时，有一解，即 x ＝ 2 ； 当 f ( x ) ＝ t 2 时，结合图象，有 3 个解 . 思维升华　 1. 上述两个题目涉及嵌套函数零点个数的判断 . 求解的主要步骤： (1) 换元解套，转化为 t ＝ g ( x ) 与 y ＝ f ( t ) 的零点 .(2) 依次解方程，令 f ( t ) ＝ 0 ，求 t ，代入 t ＝ g ( x ) 求出 x 的值或判断图象交点个数 . 2. 抓住两点： (1) 转化换元 .(2) 充分利用函数的图象与性质 . 类型 2 　求嵌套函数零点中的参数 答案　 [ － 1 ，＋ ∞ ) 解析　 设 t ＝ f ( x ) ，令 f ( f ( x )) － a ＝ 0 ，则 a ＝ f ( t ). 在同一坐标系内作 y ＝ a ， y ＝ f ( t ) 的图象 ( 如图 ). 当 a ≥ － 1 时， y ＝ a 与 y ＝ f ( t ) 的图象有两个交点 . 设交点的横坐标为 t 1 ， t 2 ( 不妨设 t 2 > t 1 ) ，则 t 1 < － 1 ， t 2 ≥ － 1. 当 t 1 < － 1 时， t 1 ＝ f ( x ) 有一解；当 t 2 ≥ － 1 时， t 2 ＝ f ( x ) 有两解 . 综上，当 a ≥ － 1 时，函数 g ( x ) ＝ f ( f ( x )) － a 有三个不同的零点 . 思维升华　 1. 求解本题抓住分段函数的图象性质，由 y ＝ a 与 y ＝ f ( t ) 的图象，确定 t 1 ， t 2 的取值范围，进而由 t ＝ f ( x ) 的图象确定零点的个数 . 2. 含参数的嵌套函数方程，还应注意让参数的取值 “ 动起来 ” ，抓临界位置，动静结合 .