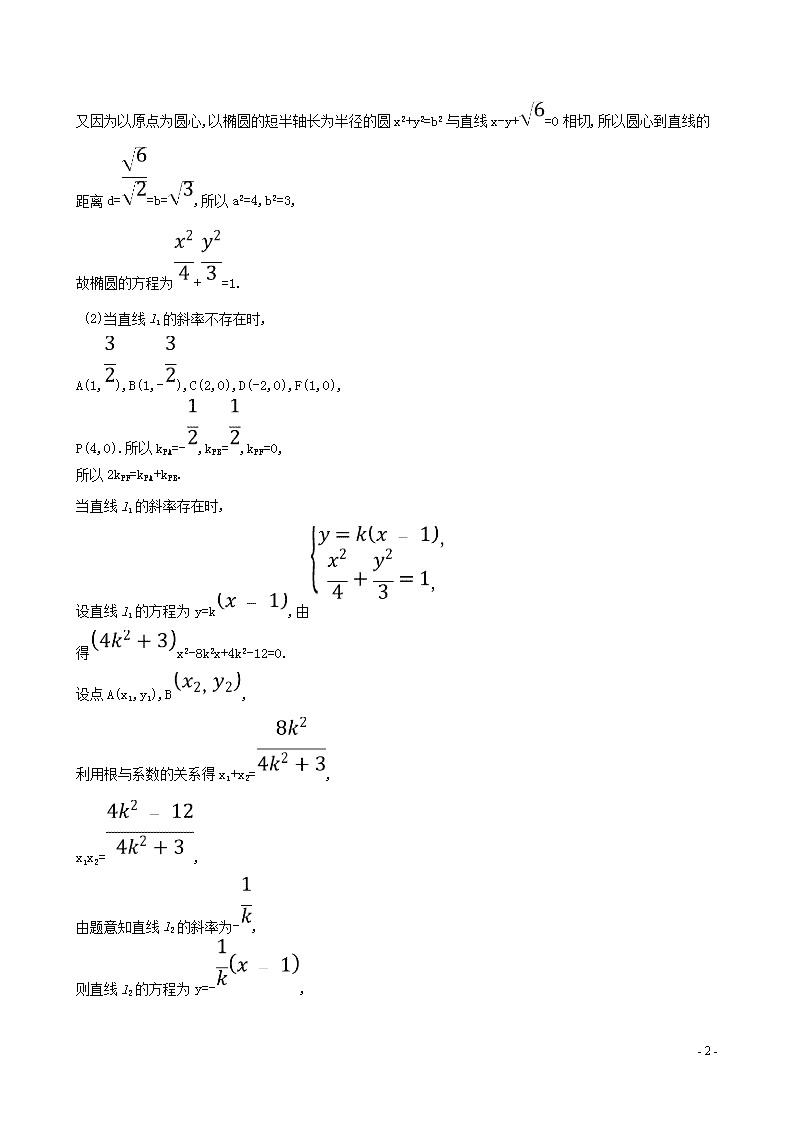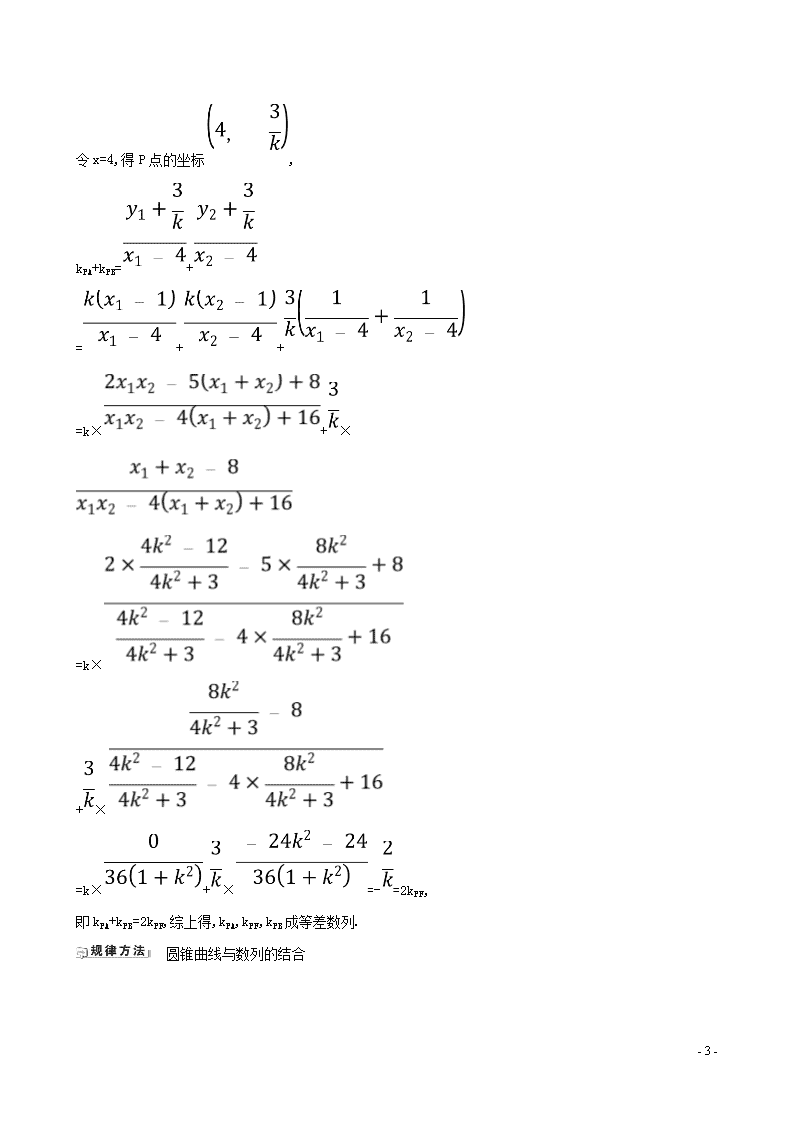高考数学一轮复习第十章平面解析几何10-10-3圆锥曲线与其他知识的交汇问题练习理北师大版

高考数学一轮复习第十章平面解析几何10-10-3圆锥曲线与其他知识的交汇问题练习理北师大版

‎10.10.3 圆锥曲线与其他知识的交汇问题 核心考点·精准研析 考点一　 圆锥曲线与数列交汇  ‎ ‎【典例】(2020·重庆模拟)已知椭圆+=1的离心率为,以原点为圆心,以椭圆的短半轴长为半径的圆与直线x-y+=0相切.‎ ‎(1)求椭圆的方程.‎ ‎(2)过椭圆的右焦点F的直线l1与椭圆交于A,B,过F与l1垂直的直线l2与椭圆交于C,D,与l3:x=4交于P,求证:直线PA,PF,PB的斜率kPA,kPF,kPB成等差数列.‎ ‎【解题导思】‎ 序号 题目拆解 ‎(1)‎ 求椭圆方程 根据离心率以及直线与圆的位置关系列出a,b的方程组求解 ‎(2)‎ ‎①求A、B两点坐标关系 研究直线和圆锥曲线的基本过程——联立方程组,根与系数的关系 ‎②求点P的坐标 联立两直线方程求解 ‎③求直线斜率,验证所证 利用两点坐标表示斜率,化所证为等式关系进行验证 ‎【解析】(1)由题意知e==,所以=,‎ 即a2=b2,‎ - 15 -‎ 又因为以原点为圆心,以椭圆的短半轴长为半径的圆x2+y2=b2与直线x-y+=0相切,所以圆心到直线的距离d==b=,所以a2=4,b2=3,‎ 故椭圆的方程为+=1.‎ ‎ (2)当直线l1的斜率不存在时,‎ A(1,),B(1,-),C(2,0),D(-2,0),F(1,0),‎ P(4,0).所以kPA=-,kPB=,kPF=0,‎ 所以2kPF=kPA+kPB.‎ 当直线l1的斜率存在时,‎ 设直线l1的方程为y=k,由 ‎ 得x2-8k2x+4k2-12=0.‎ 设点A(x1,y1),B,‎ 利用根与系数的关系得x1+x2=,‎ x1x2=,‎ 由题意知直线l2的斜率为-,‎ 则直线l2的方程为y=-,‎ - 15 -‎ 令x=4,得P点的坐标,‎ kPA+kPB=+‎ ‎=++‎ ‎=k×+×‎ ‎=k×‎ ‎+×‎ ‎=k×+×=-=2kPF,‎ 即kPA+kPB=2kPF,综上得,kPA,kPF,kPB成等差数列.‎ ‎　圆锥曲线与数列的结合 - 15 -‎ 圆锥曲线与数列的结合点比较多,如圆锥曲线中的相关线段长度或参数成等差、等比数列等,解决此类问题的关键是利用数列的知识,将条件等价转化为相关数量之间的关系即可,其实质就是相关的数量之间的等式关系的一种外在表现.‎ ‎(2019·成都模拟)设圆x2+y2-4x-60=0的圆心为F2,直线l过点F1(-2,0)且与x轴不重合,交圆F2于C,D两点,过点F1作CF2的平行线交DF2于点E.‎ ‎(1)求+的值.‎ ‎(2)设点E的轨迹为曲线E1,直线l与曲线E1相交于A,B两点,与直线x=-8相交于M点,试问在椭圆E1上是否存在一定点N,使得k1,k3,k2成等差数列(其中k1,k2,k3分别指直线AN,BN,MN的斜率).若存在,求出N点的坐标;若不存在,请说明理由.‎ ‎【解析】(1)因为圆x2+y2-4x-60=0的圆心为F2,所以=且F1E∥CF2,‎ 所以∠F2DC=∠F2CD=∠EF1D,‎ 所以=,‎ 所以+=|ED|+=,‎ 又因为圆F2的半径为8,即=8,‎ 所以+=8.‎ ‎(2)由(1)知,曲线E1是以F1,F2为焦点的椭圆,且长轴长为8,所以曲线E1的方程为+=1(y≠0),‎ 由题意,设直线l的方程为y=k(x+2),‎ 代入椭圆方程化简得x2+16k2x+16k2-48=0,‎ 设A(x1,y1),B(x2,y2),N(x0,y0),‎ 则x1+x2=-,x1x2=,‎ 所以k1+k2=+‎ - 15 -‎ ‎=‎ ‎=,‎ 因为k1,k3,k2成等差数列,所以2k3=k1+k2,‎ 因为k3=,所以2×‎ ‎=,‎ 化简得24k3-24k2y0‎ ‎+24k-24y0=0,‎ 对任意的k该等式恒成立,所以x0=-2,此时y0=±3.‎ 所以存在点N(-2,±3)使得k1,k3,k2成等差数列.‎ 考点二　圆锥曲线与向量交汇 ‎ ‎【典例】(2020·福州模拟)已知椭圆+=1(a>b>0)的左焦点为F,A,B是椭圆上关于原点O对称的两个动点,当点A的坐标为时,△ABF的周长恰为7. ‎ ‎(1)求椭圆的方程.‎ ‎(2)过点F作直线l交椭圆于C,D两点,且=λ(λ∈R),求△ACD面积的取值范围.‎ ‎【解题导思】‎ 序号 题目拆解 ‎(1)‎ 利用椭圆的定义 和对称性以及点A的坐标求a,b - 15 -‎ ‎(2)‎ ‎①求|CD|‎ 将直线方程与椭圆方程联立,建立C、D两点坐标之间的关系,利用弦长公式求解 ‎②求△ACD 面积 求出点A到CD的距离,根据三角形面积计算公式建立目标函数 ‎③求范围 根据目标函数解析式的特征,采用相应的方法,转化为函数的值域问题 ‎【解析】(1)当点A的坐标为时,‎ ‎==,所以|AB|=3.‎ 由对称性,+=2a,‎ 所以2a=7-3=4,得a=2,‎ 将点代入椭圆方程+=1中,解得b2=4, ‎ 所以椭圆方程为+=1.‎ ‎(2)当直线AB的斜率不存在时,=2,‎ 此时S△ACD=×2×2=2. ‎ 当直线AB的斜率存在时,‎ 设直线CD的方程为y=k(x+2)(k≠0).‎ 由 消去y整理得:‎ ‎(1+2k2)x2+8k2x+8k2-8=0. 显然Δ>0,‎ - 15 -‎ 设C,D,则 ‎ 故=· ‎ ‎=·‎ ‎=·=.‎ 因为=λ(λ∈R),所以CD∥AB,‎ 所以点A到直线CD的距离即为点O到直线CD的距离d=,‎ 所以S△ACD=××d=×‎ ‎==4‎ ‎=2=2,‎ 因为1+2k2>1,所以0<<1,‎ 所以0b>0)的离心率为,短轴为MN(M为上顶点).点P(4,0)满足·=15.‎ ‎(1)求椭圆C的方程.‎ ‎(2)设O为坐标原点,过点P的动直线l与椭圆交于点A、B,是否存在常数λ使得·+λ·为定值?若存在,求出λ的值;若不存在,请说明理由.‎ ‎【解析】(1)·=(-4,b)·(-4,-b)=16-b2=15,‎ 所以b=1,又e=,所以=,a2=4,‎ 从而C的方程为+y2=1.‎ ‎(2)当l不为x轴时,‎ 设l:x=my+4,A(x1,y1),B(x2,y2),‎ 联立l与C的方程可得(m2+4)y2+8my+12=0,‎ 所以y1+y2=-,y1y2=,‎ ‎·+λ·=x1x2+y1y2+λ[(x1-4)(x2-4)+y1y2]‎ ‎=(1+λ)(1+m2)y1y2+4m(y1+y2)+16=+16.‎ 因为·+λ·为定值,‎ 所以=,‎ - 15 -‎ 解得λ=,此时定值为.‎ 当l为x轴时,A(-2,0),B(2,0),·+λ·=-4+×12=.‎ 综上,存在λ=使得·+λ·为定值.‎ 考点三　圆锥曲线与导数交汇 ‎ ‎【典例】(2020·西安模拟)设定点F(0,1),动点E满足:以EF为直径的圆与x轴相切. ‎ ‎(1)求动点E的轨迹C的方程.‎ ‎(2)设A,B是曲线C上两点,若曲线C在点A,B处的切线互相垂直,求证:A,F,B三点共线.‎ ‎【解题导思】‎ 序号 题目拆解 ‎(1)‎ 直接法 将已知条件转化为点E的坐标所满足的条件,然后化简即可 ‎(2)‎ ‎①求A、B两点处的切线斜率 导数的几何意义求切线斜率 ‎②建立两点坐标关系 根据切线相互垂直建立坐标之间的关系 ‎③证明三点共线 利用有公共点的两直线斜率相等证明三点共线 ‎【解析】(1)设E,则EF的中点为M,依题意知M到点F的距离与它到x轴的距离相等,可得=,‎ 化简得x2=4y,即为动点E的轨迹C的方程.‎ ‎ (2)设A,B,‎ - 15 -‎ 则由y=得y′=,知曲线C在点A,B处的切线的斜率分别是,,依题意·=-1,即x1x2=-4,可得B,‎ 所以kAF==-,kBF = = -,‎ 所以kAF=kBF,知A,F,B三点共线.‎ 导数与圆锥曲线的结合点主要有两个方面:‎ ‎(1)利用导数的几何意义给出直线方程;‎ ‎(2)利用导数法求解圆锥曲线中的最值时,若某些目标代数式的形式比较复杂,不能直接根据基本初等函数的性质求解最值,可借助导数研究函数的单调性,进而求解其最值.‎ ‎　(2019·郑州模拟)已知动圆E经过点F(1,0),且和直线l:x=-1相切.‎ ‎(1)求该动圆圆心E的轨迹G的方程.‎ ‎(2)已知点A(3,0),若斜率为1的直线l′与线段OA相交(不经过坐标原点O和点A),且与曲线G交于B,C两点,求△ABC面积的最大值.‎ ‎【解析】(1)由题意可知点E到点F的距离等于点E到直线l的距离,所以动点E的轨迹是以F(1,0)为焦点,直线x=-1为准线的抛物线,故轨迹G的方程是y2=4x.‎ ‎(2)设直线l′的方程为y=x+m,其中-30恒成立.‎ 由根与系数的关系得 x1+x2=4-2m,x1·x2=m2,所以|CB|=4,‎ - 15 -‎ 点A到直线l′的距离d=,‎ 所以S△ABC=×4×‎ ‎=2×(3+m),‎ 令=t,t∈(1,2),则m=1-t2,‎ 所以S△ABC=2t(4-t2)=8t-2t3,‎ 令f(t)=8t-2t3,所以f′(t)=8-6t2,‎ 令f′(t)=0,得t=(负值舍去).‎ 易知y=f(t)在上单调递增,在上单调递减.所以y=f(t)在t=,‎ 即m=-时取得最大值为.‎ 所以△ABC面积的最大值为.‎ ‎【变式备选】‎ ‎1.已知平面上一动点P到定点C(1,0)的距离与它到直线l:x=4的距离之比为.‎ ‎(1)求点P的轨迹方程.‎ ‎(2)点O是坐标原点,A,B两点在点P的轨迹上,F是点C关于原点的对称点,若=λ,求λ的取值范围.‎ ‎【解析】(1)设P(x,y)是所求轨迹上的任意一点,‎ 由动点P到定点C(1,0)的距离与它到直线l:x=4的距离之比为,‎ 得=,化简得+=1,即点P的轨迹方程为+=1.‎ ‎(2)由F是点C关于原点的对称点,所以点F的坐标为(-1,0),‎ - 15 -‎ 设A(x1,y1),B(x2,y2),因为=λ,‎ 则(x1+1,y1)=λ(-1-x2,-y2),‎ 可得 , ‎ 因为+=1,即+=1　①,‎ 又由+=1,则+=λ2　 ②,‎ ‎①-②得:=1-λ2,‎ 化简得x2=,‎ 因为-2≤x2≤2,所以-2≤≤2,解得≤λ≤3,所以λ的取值范围是.‎ ‎2.已知椭圆N:+=1(a>b>0)经过点C(0,1),且离心率为.‎ ‎(1)求椭圆N的方程.‎ ‎(2)直线l:y=kx-与椭圆N的交点为A,B两点,线段AB的中点为M,是否存在常数λ,使∠AMC=λ·∠ABC恒成立,并说明理由.‎ ‎【解析】‎ ‎(1)因为椭圆N:+=1经过点C,且离心率为,所以b=1,又=,a2-c2=b2,‎ - 15 -‎ 可解得c=1,a=,焦距为2c=2,‎ 故所求椭圆的方程为+y2=1.‎ ‎ 存在常数λ=2,使∠AMC=λ∠ABC恒成立.‎ 证明如下:由 得x2-12kx-16=0,Δ>0,‎ 设A,B,‎ 则x1+x2=,x1x2=,‎ 又因为=,=,‎ 所以·=x1x2+‎ ‎=x1x2+‎ ‎=x1x2-k+‎ ‎=·-k· +=0,‎ 所以⊥,因为线段AB的中点为M,‎ 所以=,所以∠AMC=2∠ABC.‎ 存在常数λ=2,使∠AMC=λ∠ABC恒成立.‎ - 15 -‎ ‎3.(2020·福州模拟)已知椭圆C:+=1(a>b>0)的左、右两个焦点分别为F1,F2,短轴的一个端点为P,△PF1F2内切圆的半径为,设过点F2的直线l被椭圆C截得的线段为RS,当l⊥x轴时|RS|=3.‎ ‎(1)求椭圆C的标准方程.‎ ‎(2)在x轴上是否存在一点T,使得当l变化时,总有TS与TR所在直线关于x轴对称?若存在,请求出点T的坐标;若不存在,请说明理由.‎ ‎【解析】(1)由内切圆的性质,得×2c×b=×(2a+2c)×,得=.‎ 将x=c代入+=1,得y=±,所以=3.‎ 又a2=b2+c2,所以a=2,b=,‎ 故椭圆C的标准方程为+=1.‎ ‎ (2)当直线l垂直于x轴时,显然x轴上任意一点T都满足TS与TR所在直线关于x轴对称.‎ 当直线l不垂直于x轴时,假设存在T(t,0)满足条件,设l的方程为y=k(x-1),‎ R(x1,y1),S(x2,y2).‎ 联立方程 得(3+4k2)x2-8k2x+4k2-12=0,‎ 由根与系数的关系得 　①‎ 其中Δ>0恒成立,‎ 由TS与TR所在直线关于x轴对称,得kTS+kTR=0(显然TS,TR的斜率存在),‎ - 15 -‎ 即+=0.　②‎ 因为R,S两点在直线y=k(x-1)上,‎ 所以y1=k(x1-1),y2=k(x2-1),‎ 代入②得 ‎=‎ ‎=0,‎ 即2x1x2-(t+1)(x1+x2)+2t=0,③‎ 将①代入③得 ‎==0,则t=4,‎ 综上所述,存在T(4,0),使得当l变化时,总有TS与TR所在直线关于x轴对称 - 15 -‎