2020_2021学年新教材高中数学第五章三角函数5

2020_2021学年新教材高中数学第五章三角函数5

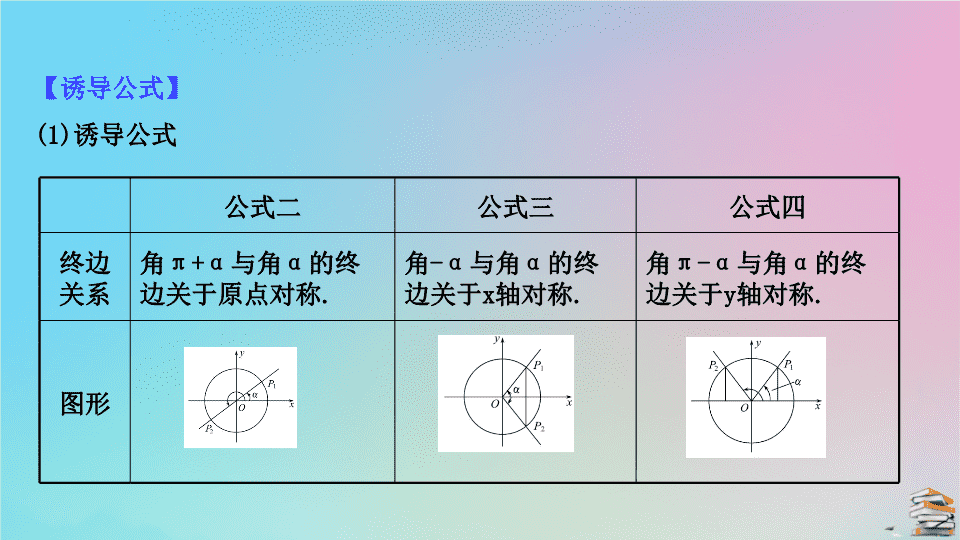
第 1 课时　诱导公式 ( 一 ) 必备知识 · 自主学习 公式二 公式三 公式四 终边关系 角 π+α 与角 α 的终 边关于原点对称 . 角 -α 与角 α 的终 边关于 x 轴对称 . 角 π-α 与角 α 的终 边关于 y 轴对称 . 图形 【 诱导公式 】 (1) 诱导公式 公式二 公式三 公式四 公式 sin( π + α )=________ ， cos( π + α )=________ ， tan( π + α )= _______. sin(- α )=________ ， cos(- α )=_______ ， tan(- α )=________. sin( π - α )=_______ ， cos( π - α )=________ ， tan( π - α )= ________. -sin α -cos α tan α -sin α cos α -tan α sin α -cos α -tan α (2) 本质：单位圆中，终边关于原点、 x 轴、 y 轴对称的角的三角函数之间的关系 . (3) 应用：通过诱导公式，将任意角的三角函数转化为锐角三角函数，广泛应用于计算、化简、证明之中 . 【 思考 】 从函数名称和符号变化两个方面观察公式一至公式四，你能发现什么规律？ 提示： 函数的名称都没有变化，符号随角的象限而变化，简记：函数名不变，符号看象限 . 【 基础小测 】 1. 辨析记忆 ( 对的打“√”，错的打“ ×”) (1) 公式一至四对任意角 α 都成立 . ( 　　 ) (2) 由公式三得 cos(α-β)=cos(β-α). ( 　　 ) (3) 在△ ABC 中， sin(A+B)=sin C. ( 　　 ) 提示： (1)×. 关于正切的公式中必须满足 α≠kπ+ ， k∈Z. (2)√.cos(α-β)=cos[-(α-β)]=cos(β-α). (3)√. 因为 A+B+C=π ，所以 A+B=π-C ，所以 sin(A+B)=sin(π-C)=sin C. 2. 已知 cos(π+θ)= ，则 cos θ= ( 　　 ) 　　　　　　　　　　　　　　　　　 A. B.- C. D.- 【 解析 】 选 B. 因为 cos(π+θ)=-cos θ= ，所以 cos θ=- . 3.( 教材二次开发：例题改编 ) 计算 sin 600°=_______ ； cos =_______ ；   tan =_______.  【 解析 】 sin 600°=sin(720°-120°)=sin(-120°)= -sin 120°=-sin(180°-60°)=-sin 60°=- . cos =cos =cos = . tan =tan =tan =1. 答案： - 　 1 类型一　给角求值问题 ( 数学运算 ) 【 题组训练 】 1.(2020· 杭州高一检测 )sin 的值等于 ( 　　 ) 　　　　　　　　　　　　　　　　　　 A. B. C.- D.- 2.cos(-2370°)= ( 　　 ) A. B.- C.- D. 关键能力 · 合作学习 3.sin ·cos ·tan = ( 　　 ) A.- B.- C. D. 　 【 解析 】 1. 选 B.sin =-sin π =-sin = sin = . 2. 选 C.cos(-2 370°)=cos(6×360°+210°)=cos(180°+30°) =-cos 30°=- . 3. 选 C. 原式 =sin · cos · tan =sin · cos · tan =sin · cos · tan = · · tan = × ×1= . 【 解题策略 】 利用诱导公式求任意角三角函数值的步骤 (1)“ 负化正”：用公式一或三来转化 . (2)“ 大化小”：用公式一将角化为 0° 到 360° 间的角 . (3)“ 小化锐”：用公式二三四将大于 90° 的角转化为锐角 . (4)“ 锐求值”：得到锐角的三角函数后求值 . 【 补偿训练 】 求下列各三角函数值： (1)sin 1 320° ； (2)cos ； (3)tan(-945°). 【 解析 】 (1) 方法一： sin 1 320°=sin(3×360°+240°)=sin 240° =sin(180°+60°)=-sin 60°=- . 方法二： sin 1 320°=sin(4×360°-120°)= sin(-120°)=-sin(180°-60°)=-sin 60°=- . (2) 方法一： cos =cos =cos =cos =-cos =- . 方法二： cos =cos =cos =-cos =- . (3)tan(-945°)=-tan 945°=-tan(225°+2×360°)=-tan 225°= -tan(180°+45°)=-tan 45°=-1. 类型二　给值 ( 式 ) 求值问题 ( 数学运算 ) 【 典例 】 1.(2020· 广州高一检测 ) 已知 sin(π+α)=- 则 tan(α-7π) 的值为 ( 　　 ) 　　　　　　　　　　　　　　　　　　 A. B.- C.1 D. 2. 已知 cos(α-75°)=- ，且 α 为第四象限角，求 sin(105°+α) 的值 . 【 思路导引 】 1. 先利用诱导公式化简已知、未知的三角函数，再用同角三角函数关系求值 . 2. 先分析所求的角与已知角的关系，再用诱导公式转化求值 . 【 解析 】 1. 选 B. 由 sin(π+α)=- ，得： sin α= ， 又 <α<π ，则 cos α=- ， 可得 ： tan( α -7 π )=tan α =- . 2. 因为 cos(α-75°)=- <0 ，且 α 为第四象限角， 所以 sin(α-75°)= = =- ， 所以 sin(105°+α)=sin[180°+(α-75°)]=-sin(α-75°)= . 【 解题策略 】 解决给值求值问题的策略 (1) 解决给值求值问题，首先要仔细观察条件式与所求式之间的角的关系，再选取恰当的诱导公式进行转化 . (2) 可以将已知式进行变形向所求式转化，或将所求式进行变形向已知式转化 . 【 跟踪训练 】 1. 若 sin(π+α)= ， α∈ ，则 tan(π-α)= ( 　　 ) A.- B.- C.- D. 【 解析 】 选 D. 因为 sin(π+α)=-sin α ，根据条件得 sin α=- ，又 α∈ ，所以 cos α= = . 所以 tan α= = =- . 所以 tan(π-α)=-tan α= . 2. 已知 cos = ，求 cos -sin 2 的值 . 【 解析 】 因为 cos =cos =-cos =- ， sin 2 =sin 2 =1-cos 2 =1- = ， 所以 cos -sin 2 =- - = . 类型三　化简求值问题 ( 数学运算、逻辑推理 ) 　角度 1 　非特殊角的化简问题  【 典例 】 计算： cos +cos +cos +cos . 【 思路导引 】 观察 与 ， 与 的关系，分别用诱导公式化简 . 【 解析 】 原式 = 【 变式探究 】 若将典例中代数式改为： tan +tan +tan +tan +tan + tan ，怎么化简？ 【 解析 】 原式 =tan +tan +tan +tan +tan + tan =tan +tan +tan -tan -tan -tan =0. 　角度 2 　复杂三角函数式的化简  【 典例 】 (2020· 长春高一检测 ) 已知 sin α=- ，且 π<α< ，求下列 各式的值： (1)tan α ； (2)(sin α+cos α) 2 + . 【 思路导引 】 (1) 利用同角三角函数的基本关系，求得 tan α 的值 . (2) 利用诱导公式、同角三角函数的基本关系，求得要求式子的值 . 【 解析 】 (1) 已知 sin α=- ，且 π<α< ， 所以 cos α=- =- ， 所以 tan α= =3. (2)(sin α+cos α) 2 + 【 解题策略 】 复杂三角函数化简的方法 (1) 先化简再求值：先化简要求的式子，明确求值方向，化简时特别注意函数符号的变化 . (2) 三角知识的综合：解题时往往还会涉及三角函数的定义，符号，同角三角函数的基本关系等知识点，要整合这些知识解题 . 【 题组训练 】 1. 角 α 的终边在直线 y=2x 上，则 = ( 　　 ) 　　　　　　　　　　　　　　　 A. B.1 C.3 D.-1 2.tan 10°+tan 170°+sin 1 866°-sin(-606°)=_______.  3. 设 k 为整数，化简： 【 解析 】 1. 选 C. 因为角 α 的终边在直线 y=2x 上， 所以 tan α =2. 所以 2. 原式 =tan 10°+tan(180°-10°)+sin(5×360°+66°)-sin[(-2)×360° +114°] =tan 10°-tan 10°+sin 66°-sin(180°-66°) =sin 66°-sin 66°=0. 答案： 0 3. 方法一： ( 分类讨论 ) 当 k 为偶数时，设 k=2m(m∈Z) ，则原式 = = = =-1 ； 当 k 为奇数时，设 k=2m+1(m∈Z) ，同理可得原式 =-1. 方法二： ( 配角法 ) 由于 kπ-α+kπ+α=2kπ ， (k+1)π+α+(k-1)π-α= 2kπ ，故 cos[(k-1)π-α]=cos[(k+1)π+α]=-cos(kπ+α) ， sin[(k+1)π+α]=-sin(kπ+α) ， sin(kπ-α)=-sin(kπ+α). 所以原式 = =-1. 【 补偿训练 】 求 (n∈Z) 的值 . 【 解析 】 ① 当 n 为奇数时，原式 = = ； ②当 n 为偶数时，原式 =sin π · cos π 课堂检测 · 素养达标 1. 已知 sin(θ+π)<0 ， cos(θ-π)>0 ，则角 θ 的终边落在 ( 　　 ) 　　　　　　　　　　　　　　　　　　 A. 第一象限 B. 第二象限 C. 第三角限 D. 第四象限 【 解析 】 选 B. 由 sin(θ+π)=-sin θ<0 ⇒ sin θ>0 ， cos(θ-π)=-cos θ>0 ⇒cos θ<0 ，由 可知 θ 是第二象限角 . 2.cos 4 260°= ( 　　 ) A. B. C.- D.- 【 解析 】 选 A.cos 4 260°=cos(360°×11+300°)=cos 300°=cos(360°- 60°)=cos(-60°)=cos 60°= . 3.( 教材二次开发：练习改编 )tan 300°+sin 450° 的值是 ( 　　 ) A.-1+ B.1+ C.-1- D.1- 【 解析 】 选 D. 原式 =tan(360°-60°)+sin(360°+90°) =tan(-60°)+sin 90°=-tan 60°+1 =- +1. 4. 已知 sin( π + α )= ，且 α 是第四象限角 ，那么 cos( α - π ) 的值是 ( 　　 ) A. B.- C.± D. 【 解析 】 选 B. 因为 sin(π+α)=-sin α= ， 所以 sin α=- . 又 α 是第四象限角，所以 cos α= ， 所以 cos(α-π)=cos(π-α)=-cos α=- . 5. =_______.  【 解析 】 =-cos α. 答案： -cos α