- 2021-06-09 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020版高中数学 第3章 不等式 3.5.2 简单线性规划
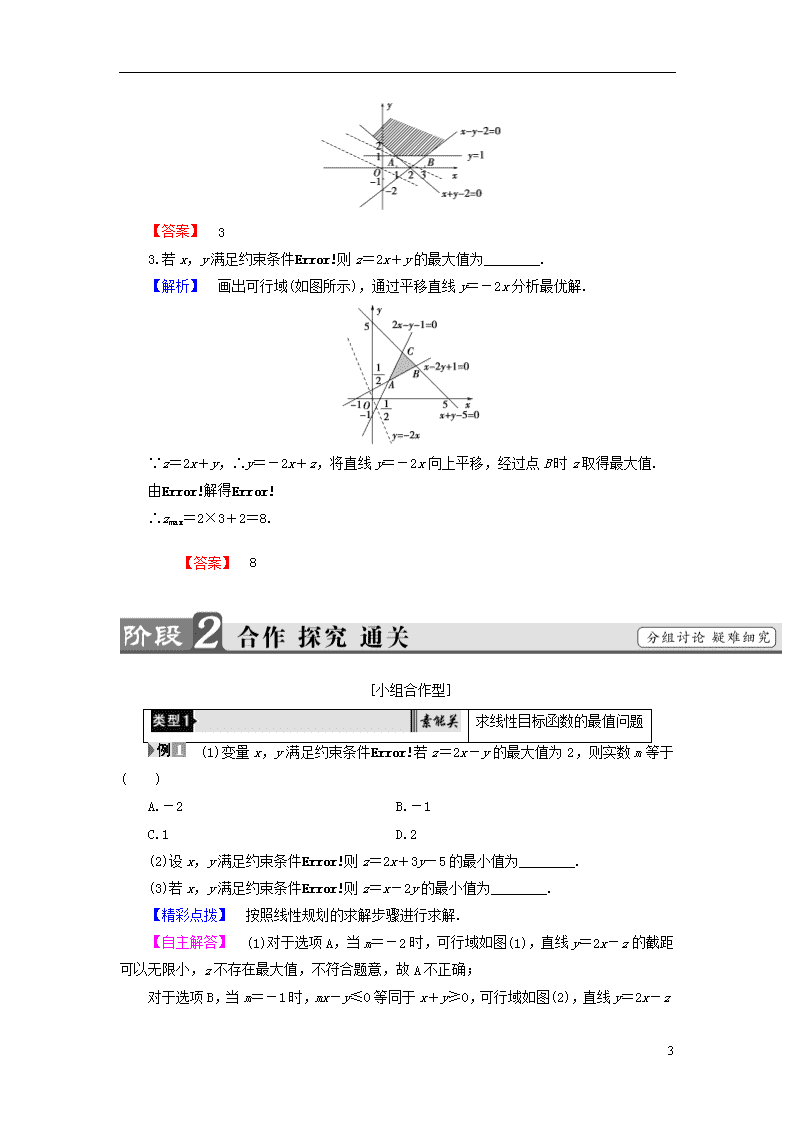
3.5.2 简单线性规划 1.了解线性规划的意义,能根据线性约束条件建立目标函数.(重点) 2.理解并初步运用线性规划的图解法解决一些实际问题.(重点、难点) 3.理解目标函数的最大、小值与其对应直线的截距的关系.(易混点) [基础·初探] 教材整理1 线性规划中的基本概念 阅读教材P90~P91例1,完成下列问题. 线性规划中的基本概念 名称 意义 约束条件 由变量x,y组成的不等式组 线性约束条件 由x,y的一次不等式(或方程)组成的不等式组 目标函数 欲求最大值或最小值所涉及的变量x,y的函数解析式 线性目标函数 关于x,y的一次解析式 可行解 满足线性约束条件的解(x,y) 可行域 所有可行解组成的集合 最优解 使目标函数取得最大或最小值的可行解 线性规划问题 在线性约束条件下求线性目标函数的最大值或最小值问题 判断(正确的打“√”,错误的打“×”) (1)可行域是一个封闭的区域.( ) (2)在线性约束条件下,最优解是唯一的.( ) (3)最优解一定是可行解,但可行解不一定是最优解.( ) (4)线性规划问题一定存在最优解.( ) 【解析】 (1)错误.可行域是约束条件表示的平面区域,不一定是封闭的. 11 (2)错误.在线性约束条件下,最优解可能有一个或多个,也可能有无数个,也可能无最优解,故该说法错误. (3)正确.满足线性约束条件的解称为可行解,但不一定是最优解,只有使目标函数取得最大值或最小值的可行解,才是最优解,所以最优解一定是可行解. (4)错误.线性规划问题不一定存在可行解,存在可行解也不一定存在最优解,故该说法是错误的. 【答案】 (1)× (2)× (3)√ (4)× 教材整理2 简单的线性规划 阅读教材P91例1~P94,完成下列问题. 线性目标函数的最值 线性目标函数z=ax+by(b≠0)对应的斜截式直线方程是y=-x+,它表示斜率为-,在y轴上的截距是的一条直线,当z变化时,方程表示一组互相平行的直线. 当b>0,截距最大时,z取得最大值,截距最小时,z取得最小值; 当b<0,截距最大时,z取得最小值,截距最小时,z取得最大值. 1.若则z=x-y的最大值为________. 【解析】 根据题意作出不等式组所表示的可行域如图阴影部分所示. 令z=0,作直线l:y-x=0.当直线l向下平移时,所对应的z=x-y的函数值随之增大,当直线l经过可行域的顶点M时,z=x-y取得最大值.顶点M是直线x+y=1与直线y=0的交点,解方程组得顶点M的坐标为(1,0),代入z=x-y,得zmax=1. 【答案】 1 2.设变量x,y满足约束条件则目标函数z=x+2y的最小值为________. 【解析】 由线性约束条件画出可行域(如图所示).由z=x+2y,得y=-x+z,z的几何意义是直线y=-x+z在y轴上的截距,要使z最小,需使z最小,易知当直线y=-x+z过点A(1,1)时,z最小,最小值为3. 11 【答案】 3 3.若x,y满足约束条件则z=2x+y的最大值为________. 【解析】 画出可行域(如图所示),通过平移直线y=-2x分析最优解. ∵z=2x+y,∴y=-2x+z,将直线y=-2x向上平移,经过点B时z取得最大值. 由解得 ∴zmax=2×3+2=8. 【答案】 8 [小组合作型] 求线性目标函数的最值问题 (1)变量x,y满足约束条件若z=2x-y的最大值为2,则实数m等于( ) A.-2 B.-1 C.1 D.2 (2)设x,y满足约束条件则z=2x+3y-5的最小值为________. (3)若x,y满足约束条件则z=x-2y的最小值为________. 【精彩点拨】 按照线性规划的求解步骤进行求解. 【自主解答】 (1)对于选项A,当m=-2时,可行域如图(1),直线y=2x-z的截距可以无限小,z不存在最大值,不符合题意,故A不正确; 对于选项B,当m=-1时,mx-y≤0等同于x+y≥0,可行域如图(2),直线y=2x-z 11 的截距可以无限小,z不存在最大值,不符合题意,故B不正确; 对于选项C,当m=1时可行域如图(3),当直线y=2x-z过点A(2,2)时截距最小,z最大为2,满足题意,故C正确; 对于选项D,当m=2时,可行域如图(4),直线y=2x-z与直线2x-y=0平行,截距最小值为0,z最大为0,不符合题意,故D不正确.故选C. (2)画出不等式组表示的平面区域如图中阴影部分所示.由题意可知,当直线y=-x++过点A(-1,-1)时,z取得最小值,即zmin=2×(-1)+3×(-1)-5=-10. (3)不等式组表示的可行域如图阴影部分所示. 由z=x-2y得y=x-z. 11 平移直线y=x,易知经过点A(3,4)时,z有最小值,最小值为z=3-2×4=-5. 【答案】 (1)C (2)-10 (3)-5 1.解二元线性规划问题的一般步骤 (1)画:在直角坐标平面上画出可行域和直线ax+by=0(目标函数为z=ax+by); (2)移:平行移动直线ax+by=0,确定使z=ax+by取得最大值或最小值的点; (3)求:求出取得最大值或最小值的点的坐标(解方程组)及最大值和最小值; (4)答:给出正确答案. 2.一般地,对目标函数z=ax+by,若b>0,则纵截距与z同号,因此,纵截距最大时,z也最大;若b<0,则纵截距与z异号,因此,纵截距最大时,z反而最小. [再练一题] 1.若x,y满足约束条件则z=x+y的最大值为________. 【解析】 不等式组表示的平面区域如图中阴影部分. 由得A. 当直线z=x+y过点A时,zmax=1+=. 【答案】 非线性目标函数的最优解问题 变量x,y满足 (1)设z=,求z的最小值; (2)设z=x2+y2,求z的取值范围. 【精彩点拨】 (1)①式子z=可进行怎样的改写? 11 ②表示的几何意义是什么? ③当倾斜角是锐角时,斜率与倾斜角的大小关系是什么? (2)①代数式x2+y2可以怎样进行改写? ②x2+y2的几何意义是什么? 【自主解答】 由约束条件 作出(x,y)的可行域如图所示. 由 解得A. 由 解得C(1,1), 由 解得B(5,2). (1)∵z==, ∴z的值即是可行域中的点与原点O连线的斜率. 观察图形可知zmin=kOB=. (2)z=x2+y2的几何意义是可行域中的点到原点O的距离的平方.结合图形可知,可行域中的点到原点的距离中,dmin=|OC|=,dmax=|OB|=, ∴2≤z≤29. 1.利用线性规划求最值,关键是理解线性目标函数的几何意义,从本题的求解过程可以看出,最优解一般在可行域的边界上,并且通常在可行域的顶点处取得,所以作图时要力求准确. 2.非线性目标函数的最值的求解策略 (1)z=(x-a)2+(y-b)2型的目标函数可转化为点(x,y)与点(a,b)距离的平方,特别地,z=x2+y2型的目标函数表示可行域内的点到原点的距离的平方. 11 (2)z=型的目标函数可转化为点(x,y)与点(a,b)连线的斜率. (3)z=|Ax+By+C|可转化为点(x,y)到直线Ax+By+C=0的距离的倍. [再练一题] 2.设x,y满足条件 【导学号:18082052】 (1)求u=x2+y2的最大值与最小值; (2)求v=的最大值与最小值. 【解】 画出满足条件的可行域如图阴影部分所示, (1)x2+y2=u表示一组同心圆(圆心为原点O),且对同一圆上的点x2+y2的值都相等,由图可知:当(x,y)在可行域内取值时,当且仅当圆O过C点时,u最大,过(0,0)时,u最小.又C(3,8),所以umax=73,umin=0. (2)v=表示可行域内的点P(x,y)到定点D(5,0)的斜率,由图可知,kBD最大,kCD最小,又C(3,8),B(3,-3), 所以vmax==,vmin==-4. [探究共研型] 利用线性规划解决实际问题 某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的倍,且对每个项目的投资不能低于5万元. 探究1 设投资甲、乙两个项目的资金分别为x、y万元,那么x、y应满足什么条件? 【提示】 探究2 若公司对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,设该公司所获利润为z万元,那么z与x,y有何关系? 【提示】 根据公司所获利润=投资项目甲获得的利润+投资项目乙获得的利润,可得z与x,y的关系为z=0.4x+0.6y. 11 探究3 x,y应在什么条件下取值,x,y取值对利润z有无影响? 【提示】 x,y必须在线性约束条件下取值.x,y取不同的值,直接影响z的取值. 某人承揽一项业务,需做文字标牌4个,绘画标牌5个.现有两种规格的原料,甲种规格每张3 m2,可做文字标牌1个,绘画标牌2个;乙种规格每张2 m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使得总用料面积最小. 【精彩点拨】 可先设出变量,建立目标函数和约束条件,转化为线性规划问题来求解. 【自主解答】 设需要甲种原料x张,乙种原料y张,则可做文字标牌(x+2y)个,绘画标牌(2x+y)个,由题意可得 所用原料的总面积为z=3x+2y, 作出可行域如图. 在一组平行直线z=3x+2y中,经过可行域内的点且到原点距离最近的直线过直线2x+y=5和直线x+2y=4的交点(2,1), ∴最优解为x=2,y=1. ∴使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小. 解答线性规划应用题的一般步骤: (1)审题——仔细阅读,对关键部分进行“精读”,准确理解题意,明确有哪些限制条件,起关键作用的变量有哪些.由于线性规划应用题中的比较多,为了理顺题目中量与量之间的关系,有时可借助表格来理顺. (2)转化——设元.写出约束条件和目标函数,从而将实际问题转化为数学上的线性规划问题. (3)求解——解这个纯数学的线性规划问题. (4)作答——就应用题提出的问题作出回答. [再练一题] 3.某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、重量、可获利润和托运能力限制数据见下表,那么为了获得最大利润,甲、乙两种货物应各托运多少箱. 11 货物 每箱体积/m3 每箱重量/kg 每箱利润/百元 甲 5 2 20 乙 4 5 10 托运能力限制数 24 13 【解】 设甲货物托运x箱,乙货物托运y箱,利润为z,由题意得z=20x+10y,作出可行域如图所示,作直线l:20x+10y=0,当直线z=20x+10y经过可行域上的点A时,z最大,又A(4.8,0)不是整点,解方程组得点B(4,1)为整点.所以甲货物托运4箱,乙货物托运1箱,可获得最大利润. 1.z=x-y在的线性约束条件下,取得最大值的可行解为( ) A.(0,1) B.(-1,-1) C.(1,0) D. 【解析】 可以验证这四个点均是可行解,当x=0,y=1时,z=-1;当x=-1,y=-1时,z=0;当x=1,y=0时,z=1;当x=,y=时,z=0.排除选项A,B,D,故选C. 【答案】 C 2.已知变量x,y满足约束条件则z=x+2y的最小值为( ) A.3 B.1 C.-5 D.-6 【解析】 由约束条件作出可行域如图: 由z=x+2y得y=-x+,的几何意义为直线在y轴上的截距,当直线y=-x+过直线x=-1和x-y=1的交点A(-1,-2)时,z最小,最小值为-5,故选C. 【答案】 C 3.已知实数x,y满足则目标函数z=x-2y的最小值是________. 11 【解析】 不等式组表示的平面区域如图阴影部分所示.目标函数可化为y=x-z,作直线y=x及其平行线,知当此直线经过点A时,-z的值最大,即z的值最小.又A点坐标为(3,6),所以z的最小值为3-2×6=-9. 【答案】 -9 4.已知点P(x,y)的坐标满足条件点O为坐标原点,那么|PO|的最小值等于________,最大值等于________. 【导学号:18082053】 【解析】 点P(x,y)满足的可行域为△ABC区域,A(1,1),C(1,3).由图可得,|PO|min=|AO|=; |PO|max=|CO|=. 【答案】 5.某公司租赁甲、乙两种设备生产A、B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元.现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元? 【解】 设需租赁甲种设备x台,乙种设备y台, 租赁费z元, 由题意得z=200x+300y. 作出如图所示的可行域. 11 令z=0,得l0:2x+3y=0, 平移l0可知,当l0过点A时,z有最小值. 又由得A点坐标为(4,5). 所以zmin=4×200+5×300=2 300. 答:该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为2 300元. 11查看更多