- 2021-06-01 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
玻尔的原子模型教案
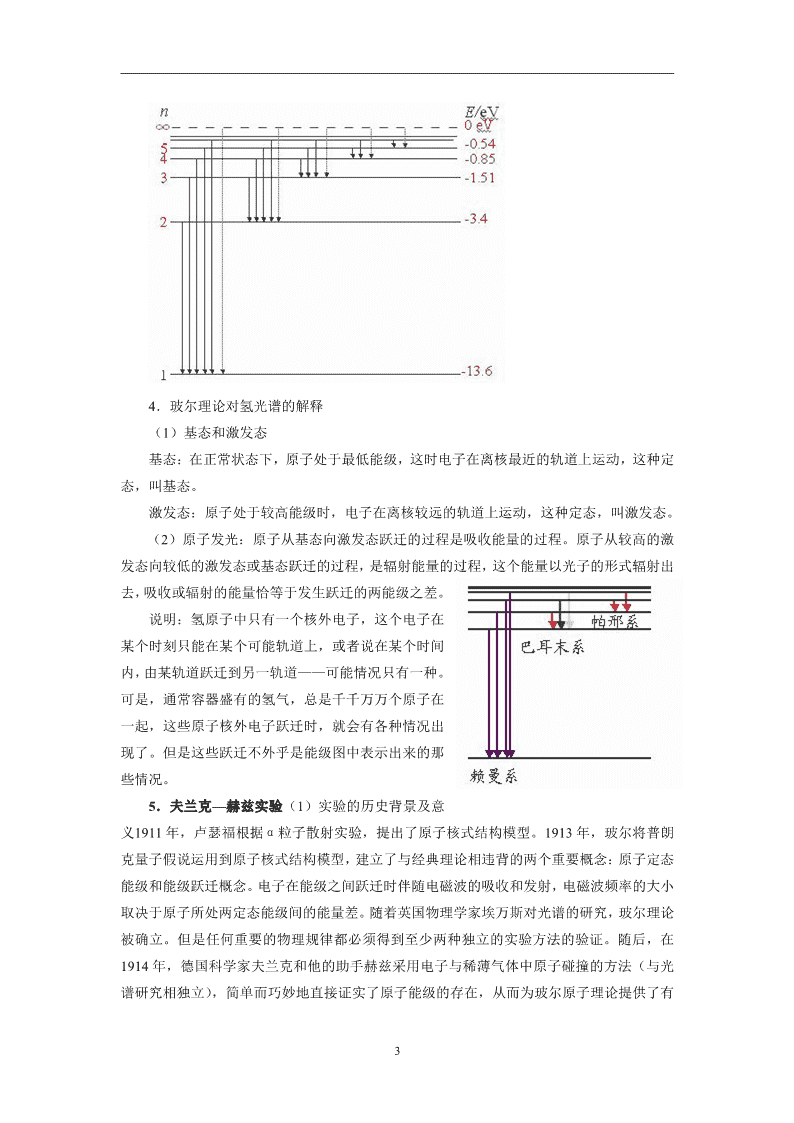
18.4 玻尔的原子模型 ★新课标要求 (一)知识与技能 1.了解玻尔原子理论的主要内容。 2.了解能级、能量量子化以及基态、激发态的概念。 (二)过程与方法 通过玻尔理论的学习,进一步了解氢光谱的产生。 (三)情感、态度与价值观 培养我们对科学的探究精神,养成独立自主、勇于创新的精神。 ★教学重点 玻尔原子理论的基本假设 ★教学难点 玻尔理论对氢光谱的解释。 ★教学方法 教师启发、引导,学生讨论、交流。 ★教学用具: 投影片,多媒体辅助教学设备 ★课时安排 1 课时 ★教学过程 (一)引入新课 复习提问: 1.α粒子散射实验的现象是什么? 2.原子核式结构学说的内容是什么? 电子绕核运动(有加速度) 辐射电磁波 频率等于绕核运行的频率 能量减少、轨道半径减少 频率变化 电子沿螺旋线轨道落入原子核 原子光谱应为连续光谱 (矛盾:实际上是不连续的亮线) 原子是不稳定的 (矛盾:实际上原子是稳定的) 3.卢瑟福原子核式结构学说与经典电磁理论的矛盾 7 教师:为了解决上述矛盾,丹麦物理学家玻尔,在1913年提出了自己的原子结构假说。 (二)进行新课 1.玻尔的原子理论 (1)能级(定态)假设:原子只能处于一系列不连续的能量状态中,在这些状态中原子是稳定的,电子虽然绕核运动,但并不向外辐射能量。这些状态叫定态。(本假设是针对原子稳定性提出的) (2)跃迁假设:原子从一种定态(设能量为En)跃迁到另一种定态(设能量为Em)时,它辐射(或吸收)一定频率的光子,光子的能量由这两种定态的能量差决定,即 (h为普朗克恒量) (本假设针对线状谱提出) (3)轨道量子化假设:原子的不同能量状态跟电子沿不同的圆形轨道绕核运动相对应。原子的定态是不连续的,因此电子的可能轨道的分布也是不连续的。(针对原子核式模型提出,是能级假设的补充) 2.玻尔根据经典电磁理论和牛顿力学计算出氢原子的电子的各条可能轨道半径和电子在各条轨道上运动时的能量(包括动能和势能)公式: 轨道半径: n=1,2,3…… 能 量: n=1,2,3…… 式中r1、E1、分别代表第一条(即离核最近的)可能轨道的半径和电子在这条轨道上运动时的能量,rn、En 分别代表第n条可能轨道的半径和电子在第n条轨道上运动时的能量,n是正整数,叫量子数。 3.氢原子的能级图 从玻尔的基本假设出发,运用经典电磁学和经典力学的理论,可以计算氢原子中电子的可能轨道半径和相应的能量。 (1)氢原子的大小:氢原子的电子的各条可能轨道的半径rn: rn=n2r1, r1代表第一条(离核最近的一条)可能轨道的半径 r1=0.53×10-10 m 例:n=2, r2=2.12×10-10 m (2)氢原子的能级:①原子在各个定态时的能量值En称为原子的能级。它对应电子在各条可能轨道上运动时的能量En(包括动能和势能) En=E1/n2 n=1,2,3,······ E1代表电子在第一条可能轨道上运动时的能量 E1=-13.6eV 注意:计算能量时取离核无限远处的电势能为零,电子带负电,在正电荷的场中为负值,电子的动能为电势能绝对值的一半,总能量为负值。 例:n=2,E2=-3.4eV, n=3,E3=-1.51eV, n=4,E4=-0.85eV,…… 氢原子的能级图如图所示。 7 4.玻尔理论对氢光谱的解释 (1)基态和激发态 基态:在正常状态下,原子处于最低能级,这时电子在离核最近的轨道上运动,这种定态,叫基态。 激发态:原子处于较高能级时,电子在离核较远的轨道上运动,这种定态,叫激发态。 (2)原子发光:原子从基态向激发态跃迁的过程是吸收能量的过程。原子从较高的激发态向较低的激发态或基态跃迁的过程,是辐射能量的过程,这个能量以光子的形式辐射出去,吸收或辐射的能量恰等于发生跃迁的两能级之差。 说明:氢原子中只有一个核外电子,这个电子在某个时刻只能在某个可能轨道上,或者说在某个时间内,由某轨道跃迁到另一轨道——可能情况只有一种。可是,通常容器盛有的氢气,总是千千万万个原子在一起,这些原子核外电子跃迁时,就会有各种情况出现了。但是这些跃迁不外乎是能级图中表示出来的那些情况。 5.夫兰克—赫兹实验 (1)实验的历史背景及意义 7 1911年,卢瑟福根据α粒子散射实验,提出了原子核式结构模型。1913年,玻尔将普朗克量子假说运用到原子核式结构模型,建立了与经典理论相违背的两个重要概念:原子定态能级和能级跃迁概念。电子在能级之间跃迁时伴随电磁波的吸收和发射,电磁波频率的大小取决于原子所处两定态能级间的能量差。随着英国物理学家埃万斯对光谱的研究,玻尔理论被确立。但是任何重要的物理规律都必须得到至少两种独立的实验方法的验证。随后,在1914年,德国科学家夫兰克和他的助手赫兹采用电子与稀薄气体中原子碰撞的方法(与光谱研究相独立),简单而巧妙地直接证实了原子能级的存在,从而为玻尔原子理论提供了有力的证据。 1925年,由于他二人的卓越贡献,他们获得了当年的诺贝尔物理学奖(1926年于德国洛丁根补发)。夫兰克-赫兹实验至今仍是探索原子内部结构的主要手段之一。所以,在近代物理实验中,仍把它作为传统的经典实验。 (2)夫兰克—赫兹实验的理论基础 根据玻尔的原子理论,原子只能处于一系列不连续的稳定状态之中,其中每一种状态相应于一定的能量值En(n=1,2,3‥),这些能量值称为能级。最低能级所对应的状态称为基态,其它高能级所对应的态称为激发态。 当原子从一个稳定状态过渡到另一个稳定状态时就会吸收或辐射一定频率的电磁波,频率大小决定于原子所处两定态能级间的能量差。 (h为普朗克恒量) 本实验中是利用一定能量的电子与原子碰撞交换能量而实现,并满足能量选择定则: (V为激发电位) 夫兰克-赫兹实验玻璃容器充以需测量的气体,本实验用的是汞。电子由阴级K发出,K与栅极G之间有加速电场,G与接收极A之间有减速电场。当电子在KG空间经过加速、碰撞后,进入KG空间时,能量足以冲过减速电场,就成为电流计的电流。 7 (3)实验原理: 改进的夫兰克-赫兹管的基本结构如下图所示。电子由阴极K发出,阴极K和第一栅极G1之间的加速电压VG1K及与第二栅极G2之间的加速电压VG2K使电子加速。在板极A和第二栅极G2之间可设置减速电压VG2A。 设汞原子的基态能量为E0,第一激发态的能量为E1,初速为零的电子在电位差为V的加速电场作用下,获得能量为eV,具有这种能量的电子与汞原子发生碰撞,当电子能量eV查看更多