高考物理二轮复习课件专题3　曲线运动

高考物理二轮复习课件专题3　曲线运动

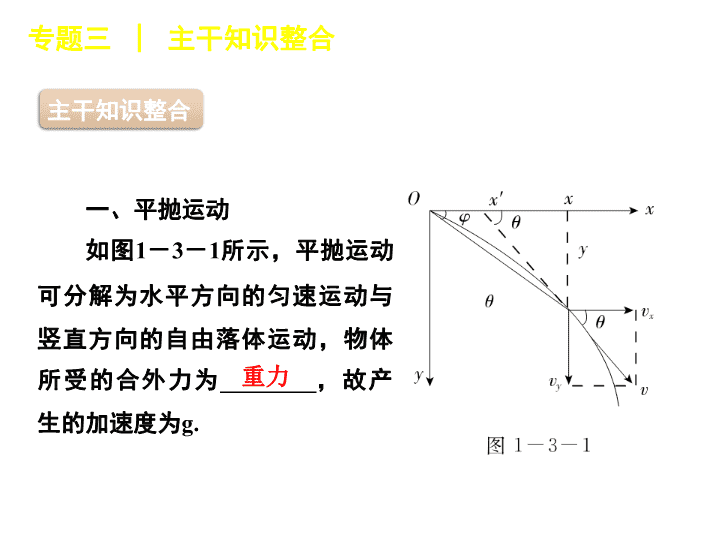
专题三曲线运动专题三　曲线运动 主干知识整合专题三│主干知识整合一、平抛运动如图1－3－1所示，平抛运动可分解为水平方向的匀速运动与竖直方向的自由落体运动，物体所受的合外力为________，故产生的加速度为g.重力 专题三│主干知识整合1．速度：vx＝v0，vy＝gt，v＝　　　　　合速度方向：tanθ＝2．位移：x＝v0t，y＝gt2，合位移大小：s＝方向：tanφ＝3．下落时间：t＝　　　　初速度：v0＝4．以上规律可以推广到类平抛运动． 物理量大小方向物理意义线速度圆弧上各点的切线方向描述质点沿圆周运动的快慢角速度中学不研究其方向周期、频率无方向专题三│主干知识整合二、匀速圆周运动1．描述圆周运动的基本参量 专题三│主干知识整合物理量大小方向物理意义向心加速度时刻指向圆心描述线速度方向改变的快慢相互关系 专题三│主干知识整合2.同一转动物体上各点的角速度相等，皮带传动轮子边缘各点的线速度大小相等．3．匀速圆周运动的向心力由物体所受________提供，两者存在着下列关系：F合＝F向或F合＝　　　　　　　　　　，但变速圆周运动一般情况下不满足上述关系．合外力 专题三│主干知识整合三、竖直平面内的变速圆周运动中的临界条件1．如图1－3－2所示，轻绳系一小球在竖直平面内做圆周运动．小球能到达最高点(刚好做圆周运动)的条件是小球在最高点时所受的重力恰好提供向心力，即：　　＝mg，这时的速度是做圆周运动的最小速度vmin＝　　　我们可称此前情景为“线－球模型”． 专题三│主干知识整合2．如图1－3－3所示，一轻杆系一小球在竖直平面内做圆周运动．小球能到达最高点(刚好做圆周运动)的条件是小球在最高点处v≥0.我们分情况讨论：当v＝0时，杆对小球的支持力等于小球的重力；当0＜v＜　　　时，杆对小球的支持力小于小球的重力；当v＝　　　时，杆对小球的支持力等于零；当v＞时，杆对小球提供________．我们可称此前情景为“杆－球模型”．拉力 专题三│主干知识整合3．由重力场与电场组成的复合场中的圆周运动如图1－3－4所示，要求细线拴着的小球能在竖直平面内做完整的圆周运动，则在最高点的速度至少为多大？ 专题三│主干知识整合此时小球受重力和电场力，平衡位置A偏离竖直位置θ角，在同一直径上另一点为B，物体受到的合力为F＝类比重力场中运动，相当于等效“重力加速度”g′＝，A为“最低点”，B为“最高点”，故小球能在竖直平面内做完整的圆周运动的条件：小球通过B点时的速度vB≥ 要点热点探究专题三│要点热点探究►　探究点一　运动的合成与分解运动的合成与分解是求解曲线运动的基本方法．运动的合成与分解实质是对描述运动的物理参量(速度、加速度、位移)进行合成与分解．合运动与分运动的关系：合运动是物体的实际运动，分运动是合运动的两个效果． 专题三│要点热点探究等时性各分运动经历的时间与合运动经历的时间相等独立性一个物体同时参与几个分运动，各个分运动独立进行，不受其他分运动的影响等效性各个分运动的规律叠加起来与合运动的规律有完全相同的效果 专题三│主干知识整合例如，平抛运动是一个合运动，是水平方向匀速直线运动和竖直方向自由落体运动的合运动，所以平抛运动的位移为合位移、速度为合速度、加速度为合加速度．准确进行运动参量的合成与分解是解决平抛运动问题的关键，同时又要注意合运动与分运动的独立性、等时性．等时性是高考命题间接给出时间关系的科学依据，所以及时利用等时性特点便成了一个解题诀窍． 专题三│要点热点探究例1某人划船渡一条河，划行速度和水流速度一定，且划行速度大于水流速度．过河的最短时间是t1；若以最小位移过河，需时间t2，则船速v1与水速v2之比为()A．t2∶t1B．t2∶C．t1∶(t1－t2)D．t1∶t2【点拨】本题考查渡河问题，注意两次渡河时间的决定因素，并准确进行速度的合成与分解． 专题三│要点热点探究例1B【解析】当小船以最短时间渡河时，船头垂直指向对岸，如图所示，过河时间t1＝　　；当船以最小位移过河时，渡河时间为t2＝　　　　　，联立可得：v1∶v2＝t2∶，选项B正确． 专题三│要点热点探究【点评】(1)合运动性质决定于合初速度与合加速度(即合外力)情况：①合加速度恒定，物体做匀变速运动；合加速度是变化的，物体做非匀变速运动．②合初速度与合加速度在一条直线上，物体做直线运动；合初速度与合加速度不在一条直线上，物体做曲线运动；(2)在运动的分解问题中，要特别注意合运动(合速度、合加速度、合位移的确定)，其判定方法：实际运动即为合运动． 专题三│要点热点探究变式题[2011·江苏卷]如图1－3－5所示，甲、乙两同学从河中O点出发，分别沿直线游到A点和B点后，立即沿原路返回到O点，OA、OB分别与水流方向平行和垂直，且OA＝OB.若水流速度不变，两人在静水中游速相等，则他们所用时间t甲、t乙的大小关系为()A．t甲t乙D．无法确定 专题三│要点热点探究 专题三│要点热点探究►　探究点二　平抛与类平抛运动1．平抛运动的处理方法是将其分解为水平方向和竖直方向的两个分运动．(1)水平方向：做匀速直线运动，vx＝v0，x＝v0t；(2)竖直方向：做自由落体运动，vy＝gt，y＝gt2.2．类平抛运动(如带电粒子在匀强电场中的偏转问题)的处理方法与平抛运动类似，可将类平抛运动分解为沿初速度v0方向(不一定水平)的匀速运动(vx＝v0，x＝v0t)和合力方向(合力大小恒定且与初速度v0方向垂直)的匀加速运动(vy＝at，y＝at2)．注意加速度方向不一定竖直向下，大小也不一定等于g. 专题三│要点热点探究例2飞镖比赛是一项极具观赏性的体育比赛项目，2010年的IDF(国际飞镖联合会)飞镖世界杯赛在上海进行．某一选手在距地面高h，离靶面的水平距离L处，将质量为m的飞镖以速度v0水平投出，结果飞镖落在靶心正上方．如只改变h、L、m、v0四个量中的一个，可使飞镖投中靶心的是(不计空气阻力)()A．适当减小v0B．适当增大hC．适当减小mD．适当减小L 专题三│要点热点探究【点拨】飞镖的运动性质如何？题中“将质量为m的飞镖以速度v0水平投出，结果飞镖落在靶心正上方”给出了哪些信息？例2A【解析】飞镖飞行中竖直方向y＝gt2，水平方向L＝v0t，得y＝　　　　　欲击中靶心使竖直位移增大，使L增大或v0减小，选项A正确． 专题三│要点热点探究【点评】平抛运动、类平抛运动处理的方法都是采用运动分解的方法，即分解为初速度方向的匀速直线运动和垂直初速度方向初速为零的匀加速直线运动，要善于将实际问题模型化，找到解决问题的关键因素，如上面例2问题的实质就是：为使飞镖击中靶心，就需要在水平射程一定的情况下减小初速度，从而增大飞镖竖直下落高度． 专题三│要点热点探究变式题一水平抛出的小球落到一倾角为θ的斜面上时，其速度方向与斜面垂直，运动轨迹如图1－3－6中虚线所示．小球在竖直方向下落的距离与在水平方向通过的距离之比为() 专题三│要点热点探究例2变式题B【解析】如图所示，平抛的末速度与竖直方向的夹角等于斜面倾角θ，根据有tanθ＝　　，则下落高度与水平射程之比为　　　　　　　　　　　　选项B正确． 专题三│要点热点探究【高考命题者说】本题考查考生的分析能力，涉及知识内容为平抛运动的基本规律，要求考生能够根据具体物理情境，灵活运用平抛运动规律分析解决问题，避免机械套用公式．设小球抛出至与斜面接触时经历的时间为t，速度大小为v，则水平分速度vx＝vsinθ，竖直分速度vy＝vcosθ.由抛体运动的规律，vy＝gt，小球在竖直方向和水平方向通过的距离分别为y＝gt2和x＝vxt，两者之比　　　　　　　　　　　　　选项B正确． 专题三│要点热点探究本题抽样统计难度为0.672，对物理得分在40分到70分的考生有较好的区分.7.8%的考生错选A,13%的考生错选B,11.5%的考生错选C项．(引自教育部考试中心2011《高考理科试题分析》第344页) 专题三│要点热点探究►　探究点三　圆周运动及其相关问题匀速圆周运动是高考要求的另一个典型曲线运动形式．对匀速圆周运动的分析应特别注意以下几点：(1)准确理解描述匀速圆周运动的参量，准确进行运动分析，找出其圆心和半径；(2)准确进行受力分析，明确向心力由谁提供；(3)应用牛顿第二定律建立动力学方程． 专题三│要点热点探究例3[2011·安徽卷]一般的曲线运动可以分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲线用一系列不同半径的小圆弧来代替．如图1－3－7甲所示，曲线上A点的曲率圆定义为：通过A点和曲线上紧邻A点两侧的两点作一圆，在极限情况下，这个圆就叫做A点的曲率圆，其半径ρ叫做A点的曲率半径．现将一物体沿与水平面成α角的方向以速度v0抛出，如图乙所示．则在其轨迹最高点P处的曲率半径是() 专题三│要点热点探究【点拨】题中研究对象通过最高点的曲率半径实质是什么？物体在最高点的速度大小如何？动力学关系如何？从题中你能发现哪些隐含信息？ 专题三│要点热点探究例3C【解析】根据运动的分解，物体斜抛到最高点P的速度vP＝v0cosα；在最高点P，物体所受重力提供向心力，根据牛顿第二定律：mg＝　　　解得：R＝故选项A、B、D错误，选项C正确． 专题三│要点热点探究【点评】本题实质为“线－球模型”通过最高点的临界问题，理解到这一点本题即迎刃而解．其他涉及圆周运动的临界问题也一定要准确掌握其相关模型，如(1)对竖直平面内圆周运动临界问题的分析要特别注意准确应用本讲中主干知识整合中对应的规律和方法，当然也可能出现涉及与绳子抗拉能力(或杆的支持能力)相关的临界问题；(2)水平面内的圆周运动往往和静摩擦力相结合命制临界问题，要特别注意观察和理解一些相关的情景和设备(例如火车拐弯涉及的轮缘与铁轨内外轨的位置关系等)，这往往成为能否迅速准确解题的关键． 专题三│要点热点探究角速度计可测量飞机、航天器、潜艇的转动角速度，其结构如图1－3－8所示．当系统绕轴OO′转动时，元件A发生位移并输出相应的电压信号，成为飞机、卫星等的制导系统的信息源．已知A的质量为m，弹簧的劲度系数为k、自然长度为l，电源的电动势为E、内阻不计．滑动变阻器总长也为l，电阻分布均匀，系统静止时滑片P在B点，当系统以角速度ω转动时，则()A．电路中电流随角速度的增大而增大B．电路中电流随角速度的减小而减小C．弹簧的伸长量为x＝D．输出电压U与ω的函数式为U＝变式题 专题三│要点热点探究 专题三│要点热点探究例3变式题CD【解析】变阻器全部连入电路，输出端接电压表，对电路电阻无影响，所以电路中电流恒定不变；系统以角速度ω转动时，对小球有kx＝mω2(l＋x)，求得x＝串联电路中分压规律有　　　　　得U＝