上海市高考数学真题卷

上海市高考数学真题卷

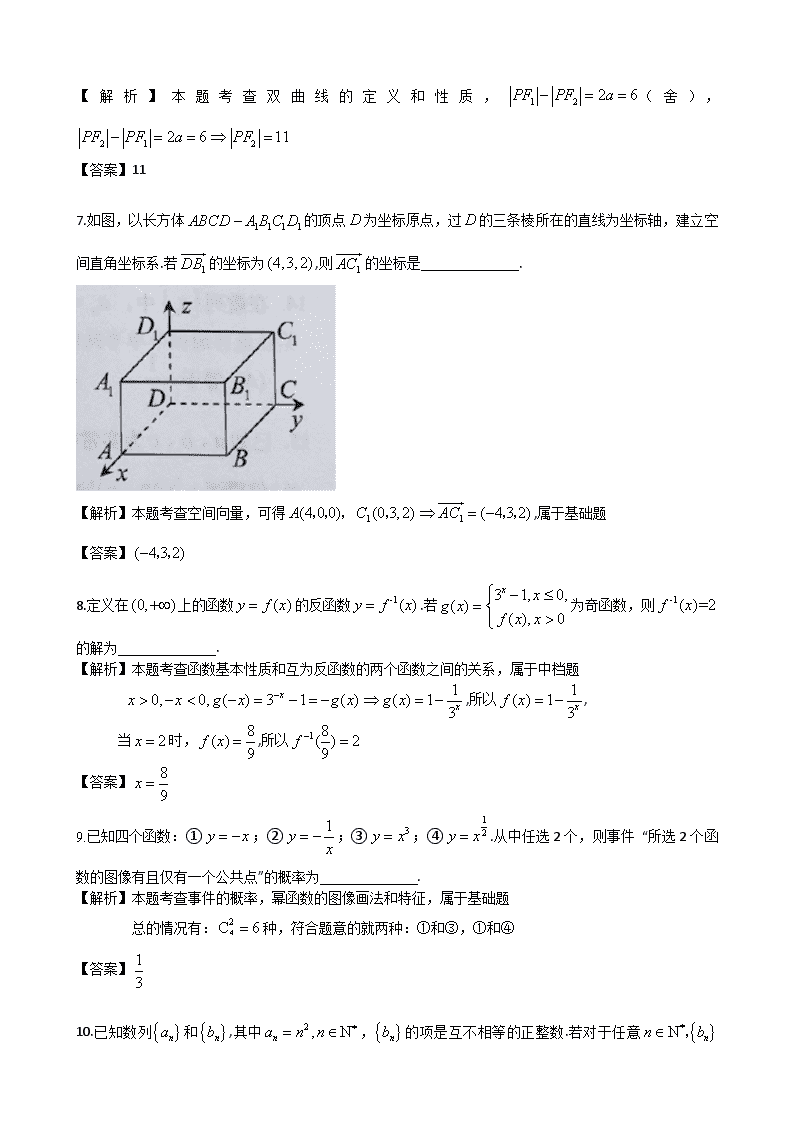
‎2017年普通高等学校招生全国统一考试上海--数学试卷 考生注意 ‎1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页.‎ ‎2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置.‎ ‎3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分.‎ ‎4.用2B铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题.‎ 一、填空题（本大题共有12题，满分54分，第1-6题每题4分，第7-12题每题5分）考生应在答题纸的相应位置直接填写结果.‎ ‎1.已知集合,则 .‎ ‎【解析】本题考查集合的运算，交集，属于基础题 ‎【答案】‎ ‎2.若排列数,则 .‎ ‎【解析】本题考查排列的计算，属于基础题 ‎【答案】3‎ ‎3.不等式的解集为 .‎ ‎【解析】本题考查分式不等式的解法，属于基础题 ‎【答案】‎ ‎4.已知球的体积为，则该球主视图的面积等于 .‎ ‎【解析】本题考查球的体积公式和三视图的概念，,‎ 所以，属于基础题 ‎【答案】‎ ‎5.已知复数满足，则 .‎ ‎【解析】本题考查复数的四则运算和复数的模，设，‎ 则,，属于基础题 ‎【答案】‎ ‎6.设双曲线的焦点为,为该双曲线上的一点.若,则 .‎ ‎【解析】本题考查双曲线的定义和性质，（舍），‎ ‎【答案】11‎ ‎7.如图，以长方体的顶点为坐标原点，过的三条棱所在的直线为坐标轴，建立空间直角坐标系.若的坐标为,则的坐标是 .‎ ‎【解析】本题考查空间向量，可得,属于基础题 ‎【答案】‎ ‎8.定义在上的函数的反函数.若为奇函数，则的解为 .‎ ‎【解析】本题考查函数基本性质和互为反函数的两个函数之间的关系，属于中档题 ‎ ,所以, ‎ 当时，,所以 ‎【答案】‎ ‎9.已知四个函数：①；②；③；④.从中任选2个，则事件 “所选2个函数的图像有且仅有一个公共点”的概率为 .‎ ‎【解析】本题考查事件的概率，幂函数的图像画法和特征，属于基础题 ‎ 总的情况有：种，符合题意的就两种：①和③，①和④‎ ‎【答案】‎ ‎10.已知数列和,其中，的项是互不相等的正整数.若对于任意 中的第项等于中的第项，则 .‎ ‎【解析】本题考查数列概念的理解，对数的运算，属于中档题 ‎ 由题意可得：，‎ ‎ 所以 ‎【答案】2‎ ‎11.设,且，则的最小值等于 .‎ ‎【解析】考查三角函数的性质和值域，，‎ 要使 ，则 ‎,当时成立 ‎【答案】‎ ‎12.如图，用35个单位正方形拼成一个矩形，点以及四个标记为“▲”的点在正方形的顶点处.设集合，点.过作直线，使得不在上的“▲”的点分布在的两侧.用和分别表示一侧和另一侧的“▲”的点到的距离之和.若过的直线中有且只有一条满足，则中所有这样的为 .‎ ‎【解析】本题考查有向距离，以左下角的顶点为原点建立直角坐标系。四个标记为“▲”的点的坐标分别为,设过点的直线为：,‎ 此时有向距离 且由 则过的直线满足;此时,直线为：：‎ 所以此时满足题意的直线为：‎ 则过的直线满足;此时有无数组解，例如：直线，直线等都满足题意.‎ 则过的直线满足;此时，直线为：,‎ 所以此时满足题意的直线为：.‎ 则过的直线满足;此时,直线为：：‎ 所以此时满足题意的直线为：‎ ‎【答案】‎ 二、选择题（本大题共有4题，满分20分，每题5分）每题有且只有一个正确选项.考生应在答题纸的相应位置，将代表正确选项的小方格涂黑.‎ ‎13.关于的二元一次方程组的系数行列式为（ ）‎ ‎ A． B． C． D．‎ ‎【答案】C ‎14.在数列，则（ ）.‎ A．等于 B．等于0 C．等于 D．不存在 ‎ ‎【答案】B ‎15．已知为实常数，数列的通项，则“存在,使得成等差数列”的一个必要条件是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎16．在平面直角坐标系中，已知椭圆和.为上的动点，为上的动点，是的最大值.记在上，在上，且，则中（ ）‎ ‎ A．元素个数为2 B．元素个数为4 C．元素个数为8 D．含有无穷个元素 ‎【答案】D 三、解答题（本大题共有5题，满分76分）解答下列各题必须在答题纸的相应位置写出必要的步骤.‎ ‎17．（本题满分14分，第1小题满分6分，第2小题满分8分）‎ 如图，直三棱柱的底面为直角三角形，两直角边和的长分别为4和2，侧棱的长为5.‎ ‎（1）求三棱柱的体积；‎ ‎（2）设是中点，求直线与平面所成角的大小。‎ ‎【答案】（1）‎ ‎（2）‎ ‎18．（本题满分14分，第1小题满分6分，第2小题满分8分）‎ 已知函数.‎ ‎（1）求的单调递增区间；‎ ‎（2）设为锐角三角形，角所对的边，角所对的边.若，求的面积.‎ ‎【答案】（1）‎ ‎（2）‎ ‎19．（本题满分14分，第1小题满分6分，第2小题满分8分）‎ 根据预测，某地第个月共享单车的投放量和损失量分别为和（单位：辆），其中.第个月底的共享单车的保有量是前个月的累计投放量与累计损失量的差.‎ ‎（1）求该地第4个月底的共享单车的保有量；‎ ‎（2）已知该地共享单车停放点第个月底的单车容纳量（单位：辆）.设在某月底，共享单车保有量达到最大，问该保有量是否超出了此时停放点的单车容纳量？‎ ‎【答案】（1）935‎ ‎ （2） ，所以当 时取最大值，为8782‎ ‎ 此时 ，所以当取最大值时，停放点不能容纳 ‎20．（本题满分16分，第1小题满分4分，第2小题满分5分，第3小题满分7分）‎ 在平面直角坐标系中，已知椭圆，为的上顶点，为上异于上、下顶点的动点.为正半轴上的动点.‎ ‎（1）若在第一象限，且，求的坐标；‎ ‎（2）设.若以为顶点的三角形是直角三角形，求的横坐标；‎ ‎（3）若,直线与交于另一点C，且，，求直线的方程.‎ ‎【答案】 （1）；‎ ‎（2）或或；‎ ‎（3）‎ 解析（3）∵点是上一动点，设，，，，，且。‎ 记线段中点为点，则 ‎∵，∴，∴，；‎ 又，∴，∴是中点，∴‎ 又∵C是上的一点，∴‎ ‎∵，∴为等腰三角形，为底边中点，∴‎ ‎∵，，‎ ‎∴‎ ‎（1）若，则，由不在上顶点可知，，为下顶点，，‎ ‎∴，无解；‎ ‎（2），则，∴‎ ‎∴‎ ‎∴或（舍），∴，∴‎ ‎∴，∴，∴直线AQ方程 ‎21．（本题满分18分，第1小题满分4分，第2小题满分6分，第3小题满分8分）‎ 设定义在上的函数满足：对于任意的，当时，都有.‎ ‎（1）若，求的取值范围；‎ ‎（2）若是周期函数，求证：是常值函数；‎ ‎（3）若恒大于零. 是定义在上的、恒大于零的周期函数，是的最大值.函数，证明：“是周期函数”的充要条件是“是常值函数”.‎ ‎【答案】（1）记，若，‎ 则，∵，∴，∴‎ ‎（2）若是周期函数，记其周期为，任取，则有 又由题意，对任意,，∴‎ 又∵，并且 所以对任意，，为常数，证毕。‎ ‎（3）充分性：若是常值函数，记，设的一个周期为，则 ‎，则对任意，，故是周期函数成立。‎ 必要性：若是周期函数，记其一个周期为。集合 任取，则必存在，使得，即，‎ ‎∴‎ 因为，，因此若 必有，且，而由第（2）问证明可知对任意，，为常数。必要性证毕。‎