高考数学浙江卷

高考数学浙江卷

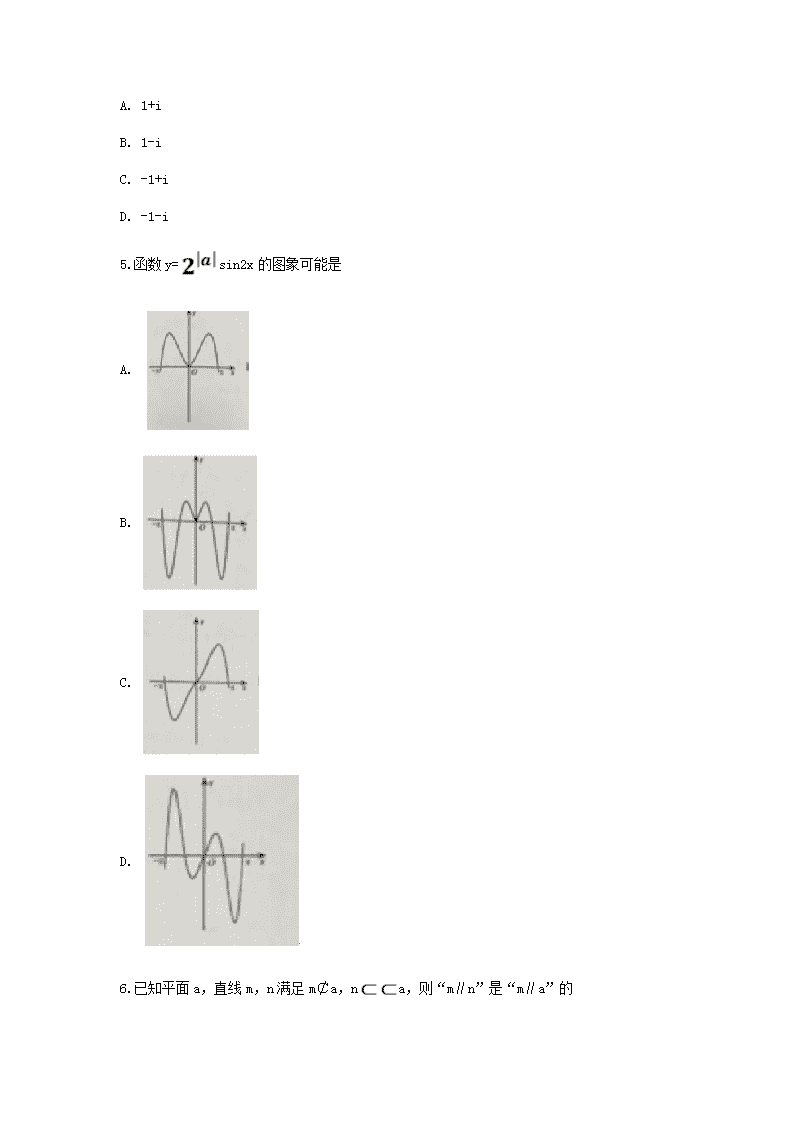
‎2018年高考数学 (浙江卷)‎ 单选题 （本大题共10小题，每小题____分，共____分。） ‎ ‎1.已知全集∪=∣1，2，3，4，5∣，A=∣1，3∣，则=‎ A. ∅‎ B. ∣1，3∣‎ C. ∣2，4，5∣‎ D. ∣1，2，3，4，5∣‎ ‎2.双曲线-y²=1的焦点坐标是 A. （-，0），（‎ B. （-2，0），（2，0）‎ C. （0，-（0，‎ D. （0，-2），（0，2）‎ ‎3.某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm ²）是 A. 2‎ B. 4‎ C. 6‎ D. 8‎ ‎4.复数（i为虚数单位）的共轭复数是 A. 1+i B. 1-i C. -1+i D. -1-i ‎5.函数y=sin2x的图象可能是 A. ‎ B. ‎ C. ‎ D. ‎ ‎6.已知平面a，直线m，n满足m￠a，na，则“m∥n”是“m∥a”的 A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 ‎7.设01）上两点A，B满足=2，则当m=____，点B横坐标的绝对值最大。‎ ‎18.解答题：本大题共5小题，共74分。解答应写出文字说明、证明过程或演算步骤。‎ ‎（本题满分14分）已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P（，）。‎ ‎（I）求sin（α+π）的值；‎ ‎（II）若角β满足sin（α+β）=，求cosβ的值。‎ ‎19．（本题满分15分）如图，已知多面体ABCA1B1C1，A1A、B1B，C1C均垂直于平面ABC，∠ABC=120度，A1A=4，C1C=1，AB=BC=B1B=2。‎ ‎（I）证明：AB1垂直平面A1B1C1；‎ ‎（II）求直线AC1与平面ABB1所成的角的正弦值 ‎20.（本题满分15分）已知等比数列{an}的公比q>1，且a3+a4+a5= 28，a4+2是a3，a5的等差中项，数列{bn}满足b1=1，数列{（bn+1-bn）an}的前n项和为2n2+n。‎ ‎（I）求q的值；‎ ‎（II）求数列{ bn}通项公式。‎ ‎21.（本题满分15分）如图，已知点P是y轴左侧（不含y轴）一点，抛物线C：y2=4x上存在不同的两点A、B满足PA、PB的中点均在C上。‎ ‎；‎ ‎（I）设AB的中点为M，证明：PM垂直于y轴；‎ ‎（II）若P是半椭圆x2+=1（x<0）上的动点，求三角形PAB面积的取值范围。‎ ‎22.（本题满分15分）已知函数f（x）= -lnx。‎ ‎（I）若f（x）在x=x1，x2（x1 x2）处导数相等，证明：f（x1）+f（x2）>8-8ln2；‎ ‎（II）若a≤3-4ln2，证明：对于任意k>0，直线y=kx+a与曲线y=f（x）有唯一公共点。‎ ‎22题 第二小题暂无答案 答案 单选题 ‎ ‎1.  C 2.  B 3.  C 4.  B 5.  D 6.  A 7.  D 8.  B 9.  A 10.  B ‎ 简答题 ‎ ‎11.  ‎ ‎12.  ‎ ‎13.  ‎ ‎14.  ‎ ‎15.  ‎ ‎16.  ‎ ‎17.  ‎ ‎18.  ‎ ‎19.  ‎ ‎20.  ‎ ‎21.  ‎ ‎22.  ‎ 解析 单选题 ‎ 略  略  略  略  略  略  略  略  略  略  ‎ 简答题 ‎ 略  略  略  略  略  略  略  略  略  略  略  略  ‎