高考数学知识点综合
2019数学高考知识点综合
【必修一】
一、 集合与函数概念
并集:由集合A和集合B的元素合并在一起组成的集合,如果遇到重复的只取一次。记作:A∪B
交集:由集合A和集合B的公共元素所组成的集合,如果遇到重复的只取一次记作:A∩B
补集:就是作差。
1、 集合的子集个数共有个;真子集有–1个;非空子集有–1个;非空的真子有–2个.
集合的中元素的三个特性: 1.元素的确定性;2.元素的互异性;3.元素的无序性
非负整数集(即自然数集)记作:N 正整数集 N*或 N+ 整数集Z 有理数集Q 实数集R
2、求的反函数:解出,互换,写出的定义域;函数图象关于y=x对称。
3、函数定义域:①分母不为0;②开偶次方被开方数;③指数的真数属于R、对数的真数.
4、函数的单调性:如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
0 , a ≠ 1 , M > 0 , N > 0,那么:
①; ②; ③。
(4)换底公式:
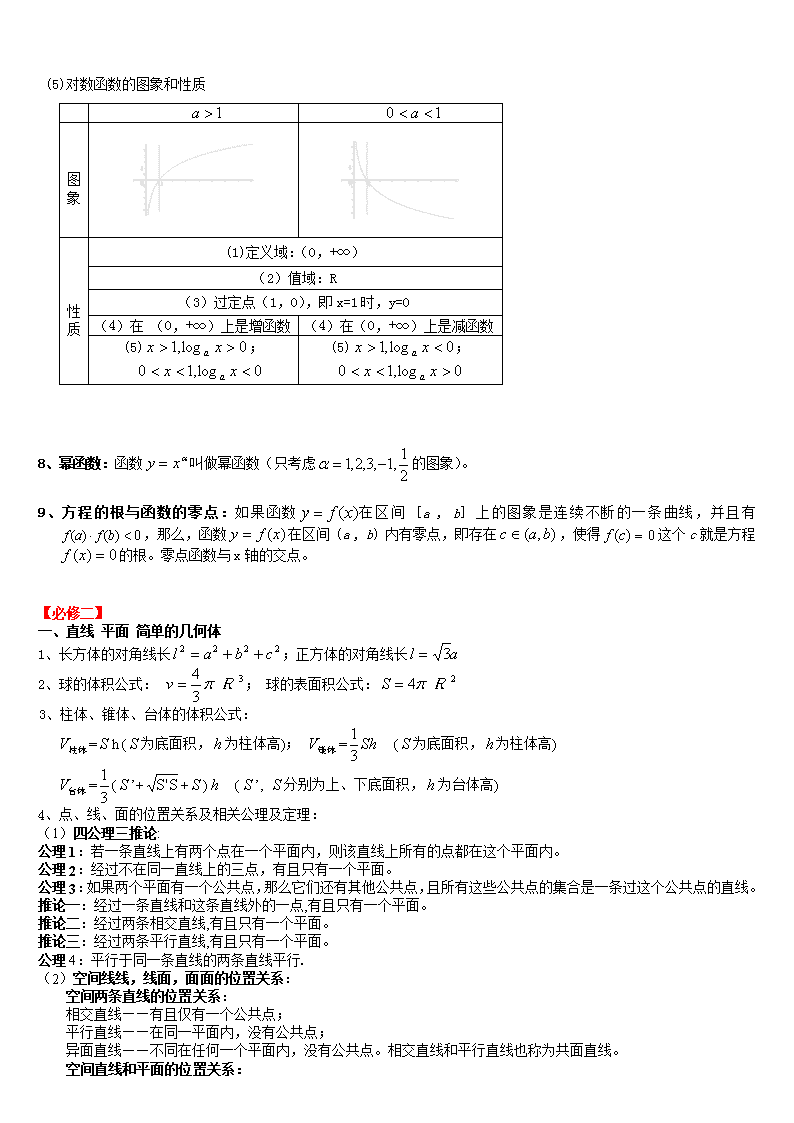
(5)对数函数的图象和性质
图
象
性
质
(1)定义域:(0,+∞)
(2)值域:R
(3)过定点(1,0),即x=1时,y=0
(4)在 (0,+∞)上是增函数
(4)在(0,+∞)上是减函数
(5);
(5);
8、幂函数:函数叫做幂函数(只考虑的图象)。
9、方程的根与函数的零点:如果函数在区间 [a , b] 上的图象是连续不断的一条曲线,并且有,那么,函数在区间 (a , b) 内有零点,即存在,使得这个c就是方程的根。零点函数与x轴的交点。
【必修二】
一、直线 平面 简单的几何体
1、长方体的对角线长;正方体的对角线长
2、球的体积公式: ; 球的表面积公式:
3、柱体、锥体、台体的体积公式:
=h (为底面积,为柱体高); = (为底面积,为柱体高)
=(’++) (’, 分别为上、下底面积,为台体高)
4、点、线、面的位置关系及相关公理及定理:
(1)四公理三推论:
公理1:若一条直线上有两个点在一个平面内,则该直线上所有的点都在这个平面内。
公理2:经过不在同一直线上的三点,有且只有一个平面。
公理3:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
推论一:经过一条直线和这条直线外的一点,有且只有一个平面。
推论二:经过两条相交直线,有且只有一个平面。
推论三:经过两条平行直线,有且只有一个平面。
公理4:平行于同一条直线的两条直线平行.
(2)空间线线,线面,面面的位置关系:
空间两条直线的位置关系:
相交直线——有且仅有一个公共点;
平行直线——在同一平面内,没有公共点;
异面直线——不同在任何一个平面内,没有公共点。相交直线和平行直线也称为共面直线。
空间直线和平面的位置关系:
(1)直线在平面内(无数个公共点);
(2)直线和平面相交(有且只有一个公共点);
(3)直线和平面平行(没有公共点)它们的图形分别可表示为如下,符号分别可表示为,,。
空间平面和平面的位置关系:
(1)两个平面平行——没有公共点;
(2)两个平面相交——有一条公共直线。
5、直线与平面平行的判定定理:如果平面外一条直线与平面内一条直线平行,那么该直线与这个平面平行。
符号表示:。图形表示:
6、两个平面平行的判定定理:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行。
符号表示:。图形表示:
7、. 直线与平面平行的性质定理:如果一条直线与一个平面平行,经过这条直线的平面与已知平面相交,那么交线与这条直线平行。
符号表示:。 图形表示:
8、两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们交线的平行。
符号表示:
9、直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么
这条直线垂直于这个平面。
符号表示:
10、.两个平面垂直的判定定理:一个平面经过另一个平面的垂线,则这两个平面垂直。
符号表示:
11、直线与平面垂直的性质:如果两条直线同垂直于一个平面,那么这两条直线平行。
符号表示:。
12、平面与平面垂直的性质:如果两个平面互相垂直,那么在其中一个平面内垂直于交线的直线垂直于另一个平面。符号表示:
13、异面直线所成角:平移到一起求平移后的夹角。
直线与平面所成角:直线和它在平面内的射影所成的角。(如右图)
14、异面直线所成角的取值范围是;
直线与平面所成角的取值范围是;
二面角的取值范围是;
两个向量所成角的取值范围是
二、直线和圆的方程
1、斜率:,;直线上两点,则斜率为
2、直线的五种方程 :
(1)点斜式 (直线过点,且斜率为).
(2)斜截式 (b为直线在y轴上的截距).
(3)两点式( (、; ()、()).
(4)截距式 (分别为直线的横、纵截距,)
(5)一般式 (其中A、B不同时为0).
3、两条直线的平行、重合和垂直:
(1)若,
①‖≠
②;
③.
(2)若,,且A1、A2、B1、B2都不为零,
①;②
4、两点P1(x1,y1)、P2(x2,y2)的距离公式 │P1P2│=
5、两点P1(x1,y1)、P2(x2,y2)的中点坐标公式 M(,)
6、点P(x0,y0)到直线(直线方程必须化为一般式)Ax+By+C=0的距离公式d=
7、平行直线Ax+By+C1=0、Ax+By+C2=0的距离公式d=
8、圆的方程:标准方程,圆心,半径为;
一般方程,(配方:)
时,表示一个以为圆心,半径为的圆;
9、点与圆的位置关系:
点与圆的位置关系有三种:
若,则
点在圆外;点在圆上;点在圆内.
10、直线与圆的位置关系:
直线与圆的位置关系有三种:
;;
.其中.
11、弦长公式:
若直线y=kx+b与二次曲线(圆、椭圆、双曲线、抛物线)相交于A(x1,y1),B(x2,y2)两点,则由
ax2+bx+c=0(a≠0)
二次曲线方程
y=kx+m
则知直线与二次曲线相交所截得弦长为:
= = =
==
13、 空间直角坐标系,两点之间的距离公式:
⑴ xoy平面上的点的坐标的特征A(x,y,0):竖坐标z=0
xoz平面上的点的坐标的特征B(x,0,z):纵坐标y=0
yoz平面上的点的坐标的特征C(0,y,z):横坐标x=0
x轴上的点的坐标的特征D(x,0,0):纵、竖坐标y=z=0
y轴上的点的坐标的特征E(0,y,0):横、竖坐标x=z=0
z轴上的点的坐标的特征E(0,0,z):横、纵坐标x=y=0
⑵│P1P2│=
14. 立体几何中求点到平面的距离
建立直角坐标系:求平面的法向量,再用两点距离公式求(法向量与该点坐标)
等体积法:将其看成一个四面体,顶点为所给点,另外三点为所给点射影平面上,将射影平面的三点构成的三角形为底面三角形,再根据=求出h(h即为点到平面的距离)
【必修三】
算法初步与统计:
以下是几个基本的程序框流程和它们的功能
图形符号
名称
功能
终端框(起止框)
表示一个算法的起始和结束
输入、输出框
表示一个算法输入输出的信息
处理框(执行框)
赋值、计算(语句、结果的传送)
判断框
判断某一条件是否成立时,在出口处标明“是”或“Y”,不成立时标明“否”或“N”
流程线
连接程序框(流程进行的方向)
连接点
连接程序框图的两部分
注释框
帮助注解流程图
循环框
程序做重复运算
一、算法的三种基本结构:(1)顺序结构(2)条件结构(3)循环结构
二、算法基本语句:1、输入语句:输入语句的格式:INPUT “提示内容”; 变量。2、输出语句:输出语句的一般格式:PRINT“提示内容”;表达式。3、赋值语句:赋值语句的一般格式:变量=表达式。4、条件语句(1)“IF—THEN—ELSE”语句。5、循环语句:直到型循环结构“DO—LOOP UNTIL”语句和当型循环结构“WHILE—WEND”。
三.三种常用抽样方法:
1、简单随机抽样;2.系统抽样;3.分层抽样。4.统计图表:包括条形图,折线图,饼图,茎叶图。
四、频率分布直方图:具体做法如下:(1)求极差(即一组数据中最大值与最小值的差);(2)决定组距与组数;
(3)将数据分组;(4)列频率分布表;(5)画频率分布直方图。注:频率分布直方图中小正方形的面积=组距×频率。
2、频率分布直方图: (注意:不是小矩形的高度)
计算公式:
各组频数之和=样本容量, 各组频率之和=1
3、茎叶图:茎表示高位,叶表示低位。
折线图:连接频率分布直方图中小长方形上端中点,就得到频率分布折线图。
4、刻画一组数据集中趋势的统计量:平均数,中位数,众数。
在一组数据中出现次数最多的数据叫做这组数据的众数;
将一组数据按照从大到小(或从小到大)排列,处在中间位置上的一个数据(或中间两位数据的平均数)叫做这组数据的中位数;
5、刻画一组数据离散程度的统计量:极差 ,极准差,方差。
(1)极差一定程度上表明数据的分散程度,对极端数据非常敏感。
(2)方差,标准差越大,离散程度越大。方差,标准差越小,离散程度越小,聚集于平均数的程度越高。
(3)计算公式:
标准差:
方差:
直线回归方程的斜率为,截距为,即回归方程为=x+(此直线必过点(,))。
6、频率分布直方图:在频率分布直方图中,各小长方形的面积等于相应各组的频率,方长方形的高与频数成正比,各组频数之和等于样本容量,频率之和等于1。
五、随机事件:在一定的条件下所出现的某种结果叫做事件。一般用大写字母A,B,C…表示.
随机事件的概率:在大量重复进行同一试验时,事件A发生的频率 总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A)。由定义可知0≤P(A)≤1,显然必然事件的概率是1,不可能事件的概率是0。
1、事件间的关系:
(1)互斥事件:不能同时发生的两个事件叫做互斥事件;
(2)对立事件:不能同时发生,但必有一个发生的两个事件叫做互斥事件;
(3)包含:事件A发生时事件B一定发生,称事件A包含于事件B(或事件B包含事件A);
(4)对立一定互斥,互斥不一定对立。
2、概率的加法公式:
(1)当A和B互斥时,事件A+B的概率满足加法公式:P(A+B)=P(A)+P(B)(A、B互斥)(2)若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B).
3、古典概型:
(1)正确理解古典概型的两大特点:1)试验中所有可能出现的基本事件只有有限个;2)每个基本事件出现的可能性相等;(2)掌握古典概型的概率计算公式:
4、几何概型:
(1)几何概率模型:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型。
(2)几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.
(3)几何概型的概率公式:
【必修四】
一、 三角函数
1、弧度制:(1)、弧度,1弧度;弧长公式: (为所对的弧长,为半径,正负号的确定:逆时针为正,顺时针为负)。
2、三角函数:
(1)、定义:
3、特殊角的三角函数值:
的角度
的弧度
—
—
4、同角三角函数基本关系式:
5、诱导公式:(众变横不变,符号看象限) 正弦上为正;余弦右为正;正切一三为正。
1、 诱导公式一: 2、 诱导公式二: 3、诱导公式三:
4、诱导公式四: 5、诱导公式五: 6、诱导公式六:
6、两角和与差的正弦、余弦、正切:
: :
: :
: :
tan+tan= tan(+)() tan-tan= tan(-)()
7、辅助角公式:
8、二倍角公式:(1)、: : :
(2)、降次公式:(多用于研究性质)
9、在四个三角函数中只有是偶函数,其它三个是寄函数。(指数函数、对数函数是非寄非偶函数)
10、在三角函数中求最值(最大值、最小值);求最小正周期;求单调性(单调第增区间、单调第减区间);求对称轴;求对称中心点都要将原函数化成标准型;
如:再求解。
11、三角函数的图象与性质:
函数
y=sinx
y=cosx
y=tanx
图象
定义域
值域
奇偶性
奇函数
偶函数
奇函数
周期性
单调性
在增
在减
在增
在减
在 增
最值
当时,
当时,
当时,
无
当时,
对称性
对称中心,
对称轴:
对称中心,
对称轴:
对称中心,
对称轴:无
12.函数的图象:
(1)用“图象变换法”作图
由函数的图象通过变换得到的图象,有两种主要途径“先平移后伸缩”与“先伸缩后平移”。
法一:先平移后伸缩
,
法二:先伸缩后平移
当函数(A>0,,)表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做这个振动的振幅;往复振动一次所需要的时间,它叫做振动的周期;单位时间内往复振动的次数,它叫做振动的频率;叫做相位,叫做初相(即当x=0时的相位)。
二、平面向量
1、平面向量的概念:
在平面内,具有大小和方向的量称为平面向量.
向量可用一条有向线段来表示.有向线段的长度表示向量的大小,箭头所指的方向表示向量的方向.
向量的大小称为向量的模(或长度),记作.
模(或长度)为的向量称为零向量;模为的向量称为单位向量.
与向量长度相等且方向相反的向量称为的相反向量,记作.
方向相同且模相等的向量称为相等向量.
2、实数与向量的积的运算律:设λ、μ为实数,那么
(1) 结合律:λ(μ)=(λμ);(2)第一分配律:(λ+μ) =λ+μ;(3)第二分配律:λ()=λ +λ.
3、向量的数量积的运算律:(1) · =· (交换律);
(2)()· = (·)=· =·();(3)()·= · +·.
4、平面向量基本定理:
如果、是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数λ1、λ2,使得 =λ1 +λ2.
不共线的向量、叫做表示这一平面内所有向量的一组基底.
5、坐标运算:(1)设,则
数与向量的积:λ,数量积:
(2)、设A、B两点的坐标分别为(x1,y1),(x2,y2),则.(终点减起点)
6、平面两点间的距离公式:(1) =
(2)向量的模||:;
(3)、平面向量的数量积: , 注意:,,
(4)、向量的夹角,则,
7、重要结论:(1)、两个向量平行: ,
(2)、两个非零向量垂直
(3)、P分有向线段的:设P(x,y) ,P1(x1,y1) ,P2(x2,y2) ,且 ,
则定比分点坐标公式 中点坐标公式
三、空间向量
1、空间向量的概念:(空间向量与平面向量相似)
在空间中,具有大小和方向的量称为空间向量.
向量可用一条有向线段来表示.有向线段的长度表示向量的大小,箭头所指的方向表示向量的方向.
向量的大小称为向量的模(或长度),记作.
模(或长度)为的向量称为零向量;模为的向量称为单位向量.
与向量长度相等且方向相反的向量称为的相反向量,记作.
方向相同且模相等的向量称为相等向量.
2、实数与空间向量的乘积是一个向量,称为向量的数乘运算.当时,与方向相同;当时,与方向相反;当时,为零向量,记为.的长度是的长度的倍.
3、设,为实数,,是空间任意两个向量,则数乘运算满足分配律及结合律.
分配律:;结合律:.
4、如果表示空间的有向线段所在的直线互相平行或重合,则这些向量称为共线向量或平行向量,并规定零向量与任何向量都共线.
5、向量共线的充要条件:对于空间任意两个向量,,的充要条件是存在实数,使.
6、平行于同一个平面的向量称为共面向量.
7、向量共面定理:空间一点位于平面内的充要条件是存在有序实数对,,使;
8、已知两个非零向量和,在空间任取一点,作,,则称为向量,的夹角,记作.两个向量夹角的取值范围是:.
9、对于两个非零向量和,若,则向量,互相垂直,记作.
10、已知两个非零向量和,则称为,的数量积,记作.即.零向量与任何向量的数量积为.
11、等于的长度与在的方向上的投影的乘积.
12、若,为非零向量,为单位向量,则有;;,,;.
13、量数乘积的运算律:;;.
14、若空间不重合两条直线,的方向向量分别为,,则,
异面垂直时.
15、若空间不重合的两个平面,的法向量分别为,,则,
.
16、直线垂直,取直线的方向向量,则向量称为平面的法向量.
。
【必修五】:
一、解三角形:(1)三角形的面积公式::
(2)正弦定理:
(3)、余弦定理:
(4)求角:
(5) 直角三角形的内切圆半径
一般三角形内切圆半径
直角三角形外接圆半径
二. 数列
1、数列的前n项和:; 数列前n项和与通项的关系:
2、 等差数列 :(1)、定义:等差数列从第2项起,每一项与它的前一项的差等于同一个常数;
性质:等差中项:若a、b、c成等差,则2b=a+c
若(、、、),则;
若(、、),则
(2)、通项公式: (其中首项是,公差是;)
(3)、前n项和: (d≠0)
(4)、等差中项: 是与的等差中项: 或,三个数成等差常设:a-d,a,a+d
3、等比数列:(1)、定义:等比数列从第2项起,每一项与它的前一项的比等于同一个常数()。
性质:等比中项:若,,成等比数列,则
若,则;
若,则
(2)、通项公式:(其中:首项是,公比是)
(3)、前n项和:
(4) 、等比中项: 是与的等比中项:, 即(或,等比中项有两个)
4、数列求和的方法:(1)套用公式法: ①等差数列求和公式:
②等比数列求和公式:
(2)裂项相消法:
(3)分组求和法:等差+等比
(4)错位相减法:等差*等比
(5)倒序相加法
三:不等式
1、重要不等式:(1) 或 (当且仅当a=b时取“=”号).
2、均值不等式:(2) 或
(当且仅当a=b时取“=”号).
一正、二定、三相等
注意:解指数、对数不等式的方法:同底法,同时对数的真数大于0;
圆锥曲线
1、椭圆:平面内与两个定点,的距离之和等于常数(大于)的点的轨迹称为椭圆
即:,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距
几何性质:
焦点的位置
焦点在轴上
焦点在轴上
图形
标准方程
轴长
短轴的长 长轴的长
顶点
、
、
焦点
、
、
焦距
对称性
关于轴、轴、原点对称
离心率
2、双曲线:平面内与两个定点,的距离之差的绝对值等于常数(小于)的点的轨迹
即:这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距几何性质:
焦点的位置
焦点在轴上
焦点在轴上
图形
标准方程
顶点
、
、
焦点
、
、
焦距
对称性
关于轴、轴对称,关于原点中心对称
离心率
渐近线方程
3、抛物线:平面内与一个定点和一条定直线的距离相等的点的轨迹.定点称为抛物线的焦点,定直线称为抛物线的准线
几何性质:
标准方程
图形
顶点
对称轴
轴
轴
焦点
准线方程
离心率