1986年(高考数学试题文理科)

1986年(高考数学试题文理科)

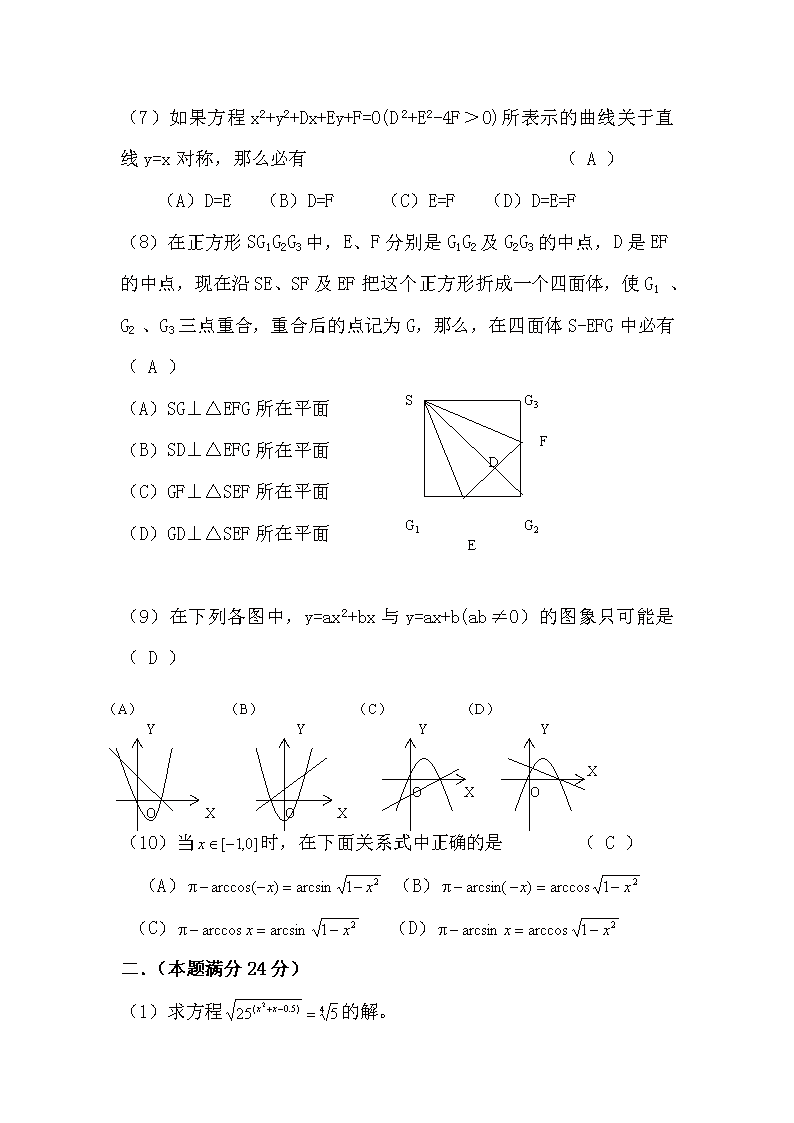
一九八六年（理科）‎ 一．（本题满分30分）‎ ‎（1）在下列各数中，已表示成三角形式的复数是 （ B ）‎ ‎ （A） （B）‎ ‎ （C） （D）‎ ‎（2）函数的反函数是 （ C ）‎ ‎ （A） （B）‎ ‎ （C） （D）‎ ‎（3）极坐标方程表示 （ B ）‎ ‎ （A）一条平行于x轴的直线 （B）一条垂直于x轴的直线 ‎ （C）一个圆 （D）一条抛物线 ‎（4）函数是 （ A ）‎ ‎ （A）周期为的奇函数 （B）周期为的偶函数 ‎ （C）周期为的奇函数 （D）周期为的偶函数 ‎（5）给出20个数： （ B ）‎ ‎87，91，94，88，93，91，89，87，92，86，90，92，88，90，91，86，89，92，95，88它们的和是 ‎ （A）1789 （B）1799 （C）1879 （D）1899‎ ‎（6）设甲是乙的充分条件，乙是丙的充要条件，丙是丁的必要条件，那么丁是甲的 （ D ）‎ ‎ （A）充分条件 （B）必要条件 ‎ （C）充要条件 （D）既不充分也不必要的条件 ‎（7）如果方程x2+y2+Dx+Ey+F=0(D2+E2-4F＞0)所表示的曲线关于直线y=x对称，那么必有 （ A ）‎ ‎ （A）D=E （B）D=F （C）E=F （D）D=E=F ‎（8）在正方形SG1G2G3中，E、F分别是G1G2及G2G3的中点，D是EF的中点，现在沿SE、SF及EF把这个正方形折成一个四面体，使G1 、G2 、G3三点重合，重合后的点记为G，那么，在四面体S-EFG中必有 （ A ）‎ S G3 ‎ ‎ ‎ ‎ F ‎ ‎ D ‎ ‎ ‎ ‎ ‎ G1 G2 ‎ ‎ E ‎ ‎（A）SG⊥△EFG所在平面 ‎（B）SD⊥△EFG所在平面 ‎（C）GF⊥△SEF所在平面 ‎（D）GD⊥△SEF所在平面 ‎（9）在下列各图中，y=ax2+bx与y=ax+b(ab≠0）的图象只可能是 （ D ）‎ ‎（A） （B） （C） （D） ‎ ‎ Y Y Y Y ‎ ‎ ‎ ‎ X ‎ ‎ O X O ‎ ‎ O X O X ‎ ‎（10）当时，在下面关系式中正确的是 （ C ）‎ ‎ （A） （B）‎ ‎ （C） （D）‎ 二．（本题满分24分）‎ ‎（1）求方程的解。‎ 答：（注：仅写出其中一个解的，给2分。）‎ ‎（2）已知的值。‎ 答：0 .‎ ‎（3）在xoy平面上，四边形ABCD的四个顶点坐标依次为（0，0）、（1，0）、（2，1）及（0，3）。求这个四边形绕x轴旋转一周所得到的几何体的体积。‎ 答：‎ ‎（4）求 答：‎ ‎（5）求展开式中的常数项。‎ 答：-40。‎ ‎（6）已知的值。‎ 答：‎ 三．（本题满分10分）‎ 如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A、B的任一点，求证：平面PAC垂直于平面PBC。‎ ‎ P ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ C ‎ ‎ ‎ ‎ A O B ‎ 证：设圆O所在平面为α，由已知条件，‎ PA⊥平面α，又BC在平面α内，‎ 因此PA⊥BC。‎ 因为∠BCA是直角，因此BC⊥AC 而PA与AC是△PAC所在平面内的相交直线，因此BC⊥△PAC所在平面，从而证得，‎ ‎△PBC所在平面与△PAC所在平面垂直。‎ 四．（本题满分12分）‎ ‎ 当sin2x＞0,求不等式的解集。‎ 解：满足sin2x＞0的x取值范围是 （1）‎ 而由得 解得：-4＜x＜-3,5＜x＜7 (5)‎ 由（1）、（5）可知所求解集为 五．（本题满分10分）‎ ‎ ‎ ‎ Y ‎ ‎ ‎ ‎ A ‎ ‎ ‎ ‎ ‎ ‎ B ‎ ‎ α ‎ ‎ β ‎ ‎ O C X ‎ 如图，在平面直角坐标系中，在y轴的正半轴（坐标原点除外）上给定两点A、B。试在x轴的正半轴（坐标原点除外）上求点C，使∠ACB取得最大值。‎ 解：设点A的坐标为（0，)、点B的坐标为（0，b），0＜b＜，又设所求点C的坐标为（x,0)‎ 记 显然，现在有 记，那么，当时，y取得最小值2。‎ 因此，当时，取得最大值 因为在内是增函数，所以当时，∠ACB取最大值 故所求点C的坐标为（0）‎ 六．（本题满分10分）‎ 已知集合A和集合B各含有12个元素，A∩B含有4个元素，试求同时满足下面两个条件的集合C的个数：（1）且C中含有3个元素，（2）（表示空集）‎ 解：因为A、B各含12个元素，A∩B含有4个元素，因此 A∪B元素的个数是12+12-4=20‎ 故满足题目条件（1）的集合的个数是，在上面集合中，还满足A∩C=的集合C的个数是 因此，所求集合C的个数是-=1084‎ ‎（解二略）‎ 七．（本题满分12分）‎ 过点M（-1，0）的直线L1与抛物线y2=4x交于P1、P2‎ 两点。记：线段P1P2的中点为P;过点P和这个抛物线的焦点F的直线为L2;L1的斜率为k。试把直线L2的斜率与直线L1的斜率之比表示为k的函数，并指出这个函数的定义域、单调区间，同时说明在每一单调区间上它是增函数还是减函数。‎ ‎ L2 ‎ ‎ Y L1 ‎ ‎ ‎ ‎ P2 ‎ ‎ ‎ ‎ P ‎ ‎ M P1 F ‎ ‎ -1 O X ‎ 解：由已知条件可知，直线L1的方程是 y=k(x+1) ①‎ 把①代入抛物线方程y2=4x，‎ 整理后得到 ‎ ②‎ 因此，直线L1与该抛物线有两个交的充要条件是：‎ ‎ ③‎ 及 ④‎ 解出③与④得到 现设点P的坐标为，‎ 则直线L1的斜率而直线L2的斜率 记则今记L1与抛物线的两个交点P1与P2的横坐标分别为x1和x2，由韦达定理及②得 显然，1-k2在（-1，0）内递增，在（0，1）内递减。所以，‎ 在（0，1）内为增函数，在（-1，0）内为减函数。‎ 八．（本题满分12分）‎ 已知x1＞0,x1≠1，且试证：数列{xn}或者对任意自然数n都满足xn＜xn+1,或者对任意自然数n都满足xn＞xn+1.‎ 证：首先，‎ 由于x1＞0，由数列{xn}的定义可知 xn＞0，（n=1,2,…）‎ 所以，xn+1-xn与1-xn2的符号相同。‎ ‎（1）假定x1<1,我们用数学归纳法证明1-xn2＞0（)‎ 显然，n=1时，1-x12＞0‎ 设n=k时1-xk2＞0,那么当n=k+1时 因此，对一切自然数n都有1-xn2＞0，‎ 从而对一切自然数n都有xn＜xn+1。‎ ‎（2）若x1＞1,用理可证，一切自然数n都有xn＞xn+1.‎ 九．（附加题，本题满分10分）‎ ‎（1）求的导数。‎ ‎（2）求过点（-1，0）并与曲线相切的直线方程。‎ 解：（1）‎ ‎（2）‎ 而点（-1，0）在曲线上，所以所求的切线方程为y=x+1‎ 一九八六年（文科）‎ 一．（本题满分30分）‎ ‎（1）在下列各数中，已表示成三角形式的复数是 （ B ）‎ ‎ （A） （B）‎ ‎ （C） （D）‎ ‎（2）函数的反函数是 （ C ）‎ ‎ （A） （B）‎ ‎ （C） （D）‎ ‎（3）已知全集I={1，2，3，4，5，6，7，8}，A={3，4，5}，B={1，3，6}，那么集合{2，7，8}是 （ D ）‎ ‎（A）A∪B （B）A∩B （C）∪ （D）∩‎ ‎（4）函数是 （ A ）‎ ‎ （A）周期为的奇函数 （B）周期为的偶函数 ‎ （C）周期为的奇函数 （D）周期为的偶函数 ‎（5）已知c<0，在下列不等式中成立的一个是 （ C ）‎ ‎ （A) (B) (C) (D)‎ ‎（6）给出20个数： （ B ）‎ ‎87，91，94，88，93，91，89，87，92，86，90，92，88，90，91，86，89，92，95，88它们的和是 ‎ （A）1789 （B）1799 （C）1879 （D）1899‎ ‎(7)已知某正方体对角线长为a，那么，这个正方体的全面积是( B )‎ ‎ （A） （B） （C） （D）‎ ‎（8）如果方程x2+y2+Dx+Ey+F=0(D2+E2-4F＞0)所表示的曲线关于直线y=x对称，那么必有 （ A ）‎ ‎ （A）D=E （B）D=F （C）E=F （D）D=E=F ‎（9）设甲是乙的充分条件，乙是丙的充要条件，丙是丁的必要条件，那么丁是甲的 （ D ）‎ ‎ （A）充分条件 （B）必要条件 ‎ （C）充要条件 （D）既不充分也不必要的条件 ‎（10）在下列各图中，y=ax2+bx与y=ax+b(ab≠0）的图象只可能是 （ D ）‎ ‎（A） （B） （C） （D） ‎ ‎ Y Y Y Y ‎ ‎ ‎ ‎ O O X ‎ ‎ X ‎ ‎ O X O X ‎ 二．（本题满分24分）‎ ‎（1）求方程的解。‎ 答：（注：仅写出其中一个解的，给2分。）‎ ‎（2）已知的值。‎ 答：0‎ ‎（3）在xoy平面上，四边形ABCD的四个顶点坐标依次为（0，0）、（1，0）、（2，1）及（0，3）。求这个四边形绕x轴旋转一周所得到的几何体的体积。‎ 答：‎ ‎（4）求 答：‎ ‎（5）求展开式中的常数项。‎ 答：-40。‎ ‎（6）求椭圆有公共焦点，且离心率为的双曲线方程。‎ 答：‎ 三．（本题满分10分）‎ 如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A、B的任一点，求证：平面PAC垂直于平面PBC。‎ ‎ P ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ C ‎ ‎ ‎ ‎ A O B ‎ 证：设圆O所在平面为α，由已知条件，‎ PA⊥平面α，又BC在平面α内，‎ 因此PA⊥BC。‎ 因为∠BCA是直角，因此BC⊥AC 而PA与AC是△PAC所在平面内的相交直线，因此BC⊥△PAC所在平面，从而证得，‎ ‎△PBC所在平面与△PAC所在平面垂直。‎ 四．（本题满分10分）‎ 求满足方程的辐角主值最小的复数Z .‎ ‎ ‎ ‎ Y ‎ ‎ 4 ‎ ‎ ‎ ‎ 3 ‎ ‎ ‎ ‎ P 2 ‎ ‎ ‎ ‎ A 1 ‎ ‎ Q ‎ ‎ -4 -3 -2 -1 O X ‎ 解：满足方程的复数在复平面上所对应的点的全体组成了如图所示的一个圆，其圆心A对应的复数为，半径为，因而圆与x轴相切于点Q，点Q对应的复数是-3。‎ 从点O作圆的另一条切线OP，P为切点，则点P所对应的复数为所求的复数。‎ ‎∵‎ 设点B对应的复数为1，∴∠BOA=1500，|OA|=，∠QOA=1800-∠BOA=300‎ ‎∵OP、OQ是同一点引出的圆的两条切线，A是圆心，‎ ‎∴∠AOP=∠QOA=300，∠QOP=2∠QOA=600，‎ ‎∠BOP=1800-∠QOP=1200，|OP|=|OA|cos∠AOP=‎ ‎∴所求的复数Z=‎ 五．（本题满分12分）‎ 已知抛物线y2=x+1，定点A（3，1），B为抛物线上任意一点，点P在线段AB上，且有BP:PA=1:2，当点B在抛物线上变动时，求点P的轨迹方程，并指出这个轨迹为那种曲线。‎ 解：设点B的坐标（X,Y)，点P的坐标为（x,y)，则 ‎ ‎ ‎ Y ‎ ‎ ‎ ‎ B ‎ ‎ · P ‎ ‎ A ‎ ‎ ‎ ‎ O X ‎ 因此轨迹为抛物线。‎ 六．（本题满分10分）‎ 甲、乙、丙、丁四个公司承包8项工程，甲公司承包3项，乙公司承包1项，丙、丁两个公司各承包2项，问共有多少种承包方式。‎ 略解：共有：（种）‎ ‎（注：原解答要求分步说明，直接给出上式只给8分）‎ 七．（本题满分12分）‎ 已知sinA+sin3A+sin5A=,cosA+cos3A+cos5A=b.‎ 求证：（1）当b≠时，tg3A=.‎ ‎(2)‎ 证：由已知sinA+sin3A+sin5A=,利用和差化积公式得 ‎2sin3Acos2A+sin3A=,∴sin3A(1+2cos2A)=,①‎ 又由已知cosA+cos3A+cos5A=b，利用和差化积公式得 ‎2cos3Acos2A+cos3A=b, ∴cos3A(1+2cos2A)=b,②‎ 当b≠时，①÷②得从而证得tg3A=.‎ 又①2+②2得 sin23A(1+2cos2A)2+cos23A(1+2cos2A)2=2+b2,‎ ‎∴(1+2cos2A)2(sin23A+ cos23A)=2+b2,‎ ‎∴‎ 八．（本题满分12分）‎ 已知数列{n},其中且当n≥3时，‎ ‎（1）求数列{n}的通项公式。‎ ‎（2）求 解：（1）设则由已知条件得所以数列{n}组成了一个公比为的等比数列，其首项