艺术班高考数学基础知识专题训练24套
基础知识专题训练01
一、考试要求
集合
内 容
等级要求
A
B
C
集合及其表示
√
子集
√
交集、并集、补集
√
二 .基础知识
1、理解集合中的有关概念
(1)集合中元素的特征: 、 、
(2)集合与元素的关系用符号,表示。
(3)常用数集的符号表示:自然数集 ;正整数集;整数集 ;有理数集 、实数集 。
(4)集合的表示法: 、 、
注意:区分集合中元素的形式:如:;;;;
(5)空集是指不含任何元素的集合。(、和的区别;0与三者间的关系)
空集是任何集合的子集,是任何非空集合的真子集。(注意:,讨论时不要遗忘了的情况。)
2、集合间的关系及其运算
(1)符号“”是表示元素与集合之间关系的,立体几何中的体现 点与直线(面)的关系 ;
符号“”是表示集合与集合之间关系的,立体几何中的体现 面与直线(面)的关系 。
(2);;
(3)对于任意集合,则:
①;;;
② ; ;
; ;
3、集合中元素的个数的计算:
若集合中有个元素,则集合的所有不同的子集个数为_________,所有真子集的个数是__________,所有非空真子集的个数是 。
三.基础训练
1.设集合,则等于 ( )
A、{1,2} B、{3,4} C、{1} D、{-2,-1,0,1,2}
2.已知全集,集合,,则集合( )
A. B. C. D.
3. 已知集合,,则等于 ( )
A. B.R C. D.
4.设,则( )
5. 已知集合满足, 则集合的个数是( )
A. 1 B. 2 C. 3 D. 4
6. A=,则A Z 的元素的个数 .
7. 满足的集合M有 个
8、集合是单元素集合,则实数a=
9. 集合____________________.
10. 已知集合M= ,集合为自然对数的底数),则=
11..已知集合等于
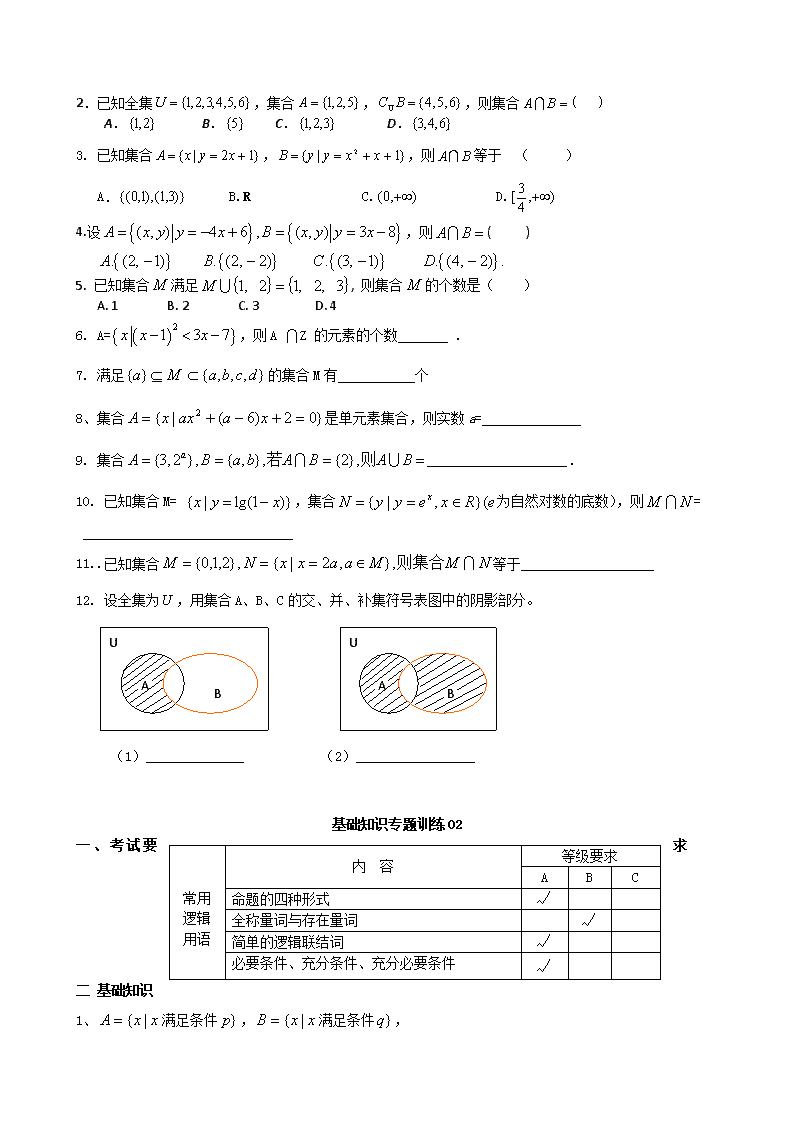
12. 设全集为,用集合A、B、C的交、并、补集符号表图中的阴影部分。
A
B
U
A
B
U
(1)______________ (2)_________________
基础知识专题训练02
常用逻辑用语
内 容
等级要求
A
B
C
命题的四种形式
√
全称量词与存在量词
√
简单的逻辑联结词
√
必要条件、充分条件、充分必要条件
√
一、考试要求
二 基础知识
1、满足条件,满足条件,
若 ;则是的充分非必要条件;
若 ;则是的必要非充分条件;
2、原命题与逆否命题,否命题与逆命题具有相同的 ;
注意:“若,则”在解题中的运用,
如:“”是“”的 条件。
3.全称量词与存在量词
⑴全称量词-------“所有的”、“任意一个”等,用表示;
全称命题p:; 全称命题p的否定p:。
⑵存在量词--------“存在一个”、“至少有一个”等,用表示;
特称命题p:; 特称命题p的否定p:;
4. (1)要理解“充分条件”“必要条件”的概念:当“若p则q”形式的命题为真时,就记作pq,称p是q的充分条件,同时称q是p的必要条件,因此判断充分条件或必要条件就归结为判断命题的真假.
(2)要理解“充要条件”的概念,对于符号“”要熟悉它的各种同义词语:“等价于”,“当且仅当”,“必须并且只需”,“……,反之也真”等.
(3)数学概念的定义具有相称性,即数学概念的定义都可以看成是充要条件,既是概念的判断依据,又是概念所具有的性质.
(4)从集合观点看,若AB,则A是B的充分条件,B是A的必要条件;若A=B,则A、B互为充要条件.
(5)证明命题条件的充要性时,既要证明原命题成立(即条件的充分性),又要证明它的逆命题成立(即条件的必要性).
三.基础训练
1. 命题“”的否命题是( )
A. B.若,则
C. D.
2.已知原命题:“若,则关于的方程有实根,”下列结论中正确的是 ( )
A.原命题和逆否命题都是假命题 B.原命题和逆否命题都是真命题
C.原命题和逆命题都是真命题 D.原命题是假命题,逆命题是真命题
3.已知命题,命题的解集是,下列结论:
①命题“”是真命题; ②命题“”是假命题;
③命题“”是真命题; ④命题“”是假命题
其中正确的是( )
A.②③ B.①②④ C.①③④ D.①②③④
4.有关命题的说法错误的是 ( )
A.命 题“若 则 ”的 逆 否 命 题 为:“若, 则”.
B.“”是“”的充分不必要条件.
C.若为假命题,则、均为假命题.
D.对于命题:使得. 则: 均有.
5.如果命题“且”是假命题,“非”是真命题,那么( )
A.命题一定是真命题 B.命题一定是真命题
C.命题一定是假命题 D.命题可以是真命题也可以是假命题
6. “”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.命题“若函数(a>0,a≠1)在其定义域内是减函数,则<0”的逆否命题是( )
A.若<0,则函数(a>0,a≠1)在其定义域内不是减函数
B.若≥0,则函数(a>0,a≠1)在其定义域内不是减函数
C.若<0,则函数(a>0,a≠1)在其定义域内是减函数
D.若≥0,则函数(a>0,a≠1)在其定义域内是减函数
8. 已知命题,,则
9. 命题“,有”的否定是 .
10. 若命题“x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为 .
11. 命题;命题 是的 条件.
12. 已知非零向量则是的 条件
13. =-1是直线和直线垂直的________________条件
14.设,是定义在R上的函数,,则“,均为偶函数”是“为偶函数”的 条件
基础知识专题训练03
一、考试要求
内 容
等级要求
函数概念与基本初等函数
A
B
C
函数的有关概念
√
函数的基本性质
√
二 .基础知识
1、函数的概念 ;
2、函数的三要素: , , 。
(1)函数解析式的求法:
①定义法(拼凑):②换元法:③待定系数法:④赋值法:
(2)函数定义域的求法:
①; ②;③; ④;
(3)函数值域的求法;
①配方法:②分离常数法(或求导)如:;④换元法;⑤三角有界法;
⑥基本不等式法;⑦单调性法; ⑧数形结合等;
3、函数的性质:
(1)单调性:定义();注意定义是相对与某个具体区间而言。判定方法:定义;导数;复合函数和图像。
(2)奇偶性:定义();注意区间是否关于原点对称,比较f(x) 与f(-x)的关系。
f(x) -f(-x)=0 f(x) =f(-x) f(x)为偶函数图像 关于()对称;
f(x)+f(-x)=0 f(x) =-f(-x) f(x)为奇函数图像 关于()对称。
(3)周期性:若函数f(x)对定义域内的任意x满足:f(x+T)=f(x),则T为函数f(x)的周期(T为非零常数)
4、函数图像变换:(1)平移变换 ;(2)对称变换 ;(3)伸缩变换
三.基础训练
1.设则的值为( )
A. B. C. D.
2. 下列函数中,在区间上是增函数的是( )
A. B. C. D.
3.若偶函数在上是增函数,则下列关系式中成立的是( )
A. B.
C. D.
4.已知其中为常数,若,则的值等于( )
A. B. C. D.
d
d0
t0 t
O
A.
d
d0
t0 t
O
B.
d
d0
t0 t
O
C.
d
d0
t0 t
O
D.
5.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程. 在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
6.下列函数中,在其定义域内既是奇函数又是减函数的是 ( )
(A) (B)
(C) (D)
7.若函数,则= .
8.函数的定义域 。
9.函数的最小值是_________________。
10.若函数是偶函数,则的递减区间是 .
11.若函数在上是减函数,则的取值范围为__________。
12、函数的图象与直线交点的个数为 个。
13.函数f(x)=(x-1)的奇偶性___;
14.为奇函数,则实数=____
15.已知,则的解析式为____________________
基础知识专题训练04
一、考试要求
函数概念与基本初等函数
内 容
等级要求
A
B
C
指数与对数
√
指数函数的图象和性质
√
对数函数的图象和性质
√
二 .基础知识
1.指数函数:
指数运算法则: ; ; 。
指数函数:y= (a>o,a≠1),图象恒过点(0,1),单调性与a的值有关,在解题中,往往要对a分a>1和0
o,a≠1) 图象恒过点(1,0),单调性与a的值有关,在解题中,往往要对a分a>1和00 C.k>0,b>0 D.k>0,b<0
10.在下列图象中,二次函数与指数函数的图象只可能是( )
x
y
o
-1
1
x
y
o
1
1
x
o
-1
1
x
y
o
1
1
A. B. C. D.
11、函数的图象与的图象关于直线对称,则的值为________
12、已知,则_____________.
基础知识专题训练05
函数概念与基本初等函数
内 容
等级要求
A
B
C
幂函数
√
函数与方程
√
一、考试要求
二 .基础知识
1常用的初等函数:
(1)一元一次函数:,当时,是增函数;当时,是减函数;
(2)一元二次函数:一般式:;对称轴方程是 ;顶点为 ;
两点式:;对称轴方程是 ;与轴的交点为 ;
顶点式:;对称轴方程是 ;顶点为 ;
①一元二次函数的单调性:
当时: 为增函数; 为减函数;当时: 为增函数; 为减函数;
②二次函数求最值问题:首先要采用配方法,化为的形式,
Ⅰ、若顶点的横坐标在给定的区间上,则
时:在顶点处取得最小值,最大值在距离对称轴较远的端点处取得;
时:在顶点处取得最大值,最小值在距离对称轴较远的端点处取得;
Ⅱ、若顶点的横坐标不在给定的区间上,则
时:最小值在距离对称轴较近的端点处取得,最大值在距离对称轴较远的端点处取得;
时:最大值在距离对称轴较近的端点处取得,最小值在距离对称轴较远的端点处取得;
有三个类型题型:(1)顶点固定,区间也固定。如:
(2)顶点含参数(即顶点变动),区间固定,这时要讨论顶点横坐标何时在区间之内,何时在区间之外。
(3)顶点固定,区间变动,这时要讨论区间中的参数.
③二次方程实数根的分布问题: 设实系数一元二次方程的两根为;则:
根的情况
等价命题
在区间上有两根
在区间有两根
在区间或有一根
充要条件
注意:若在闭区间讨论方程有实数解的情况,可先利用在开区间上实根分布的情况,得出结果,在令和检查端点的情况。
2.指数函数:
函数
y=xn
n>0
n<0
y=x
y=x2
y=x3
y=x-1
定义域
R
R
R
[0,+∞]
{x|x≠0}
值域
R
[0,+∞)
R
[0,+∞)
{y|y≠0}
图像
幂函数的性质:所有幂函数在_______________都有定义,并且图象都过点,因为,所以在第________象限无图象;
3.函数与方程
(1)方程f(x)=0有实根 函数f(x)的图像与x轴有交点 函数y=f(x)有零点。
(2)函数在区间[a,b]上的图像是连续的,且f(a)f(b)<0,那么函数f(x)在区间[a,b]
上至少有一个零点。
三.基础训练
1、函数的单调递减区间是 ( )
A、 B、 C、 D、
2、函数的图象可以看成由幂函数( )得到的。
A. 向左平移1个单位 B. 向上平移1个单位
C. 向右平移1个单位 D. 向下平移1个单位
3.二次函数y=x2+2x-7的函数值是8,那么对应的x的值是( )
A.3 B.5 C.-3和5 D.3和-5
4.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )
x
y
O
D
x
y
O
C
x
y
O
B
x
y
O
A
5.已知函数f (x)在区间 [a,b]上单调,且f (a)•f (b)<0,则方程f (x)=0在区间[a,b]内( ).
A.至少有一实根 B.至多有一实根 C.没有实根 D.必有惟一实根
6.若函数的一个正数零点附近的函数值用二分法计算,其参考数据如下:
f(1)=-2
f(1.5)=0.625
f(1.25)=-0.984
f(1.375)=-0.260
f(1.4375)=0.162
f(1.40625)=-0.054
那么方程的一个近似根(精确到0.1)为( ).
A. 1.2 B. 1.3 C. 1.4 D. 1.5
7. 方程的根所在的区间是( ).
A.(1,2) B. (2,3) C. (3,4) D.(0,1)
8.抛物线y=2x2+4x+5的对称轴是x=____ .
9.二次函数的最小值是_____________.
10、函数是幂函数,且在区间上为减函数,
则m=。
11.函数的最小值是_________________。
基础知识专题训练06
一、考试要求
内 容
等级要求
不等式
A
B
C
不等式性质
√
基本不等式
√
二 .基础知识
一、不等式的基本性质:
①若ab>0,则。即不等式两边同号时,不等式两边取倒数,不等号方向要改变。
②如果对不等式两边同时乘以一个代数式,要注意它的正负号,如果正负号未定,要注意分类讨论。
③图象法:利用有关函数的图象(指数函数、对数函数、二次函数、三角函数的图象),直接比较大小。
④中介值法:先把要比较的代数式与“0”比,与“1”比,然后再比较它们的大小
二、均值不等式:两个数的算术平均数不小于它们的几何平均数。
若,则(当且仅当时取等号)
基本变形:① ; ;
②若,则,
基本应用:①放缩,变形;
②求函数最值:注意:①一正二定三取等;②积定和小,和定积大。
当(常数),当且仅当 时, ;
当(常数),当且仅当 时, ;
常用的方法为:拆、凑、平方;
三.简单的绝对值不等式
解绝对值不等式的常用方法:
①讨论法:讨论绝对值中的式于大于零还是小于零,然后去掉绝对值符号,转化为一般不等式;
②等价变形:解绝对值不等式常用以下等价变形:
|x|0),|x|>ax2>a2x>a或x<-a(a>0)。
一般地有:|f(x)|g(x)f(x)>g (x)或f(x)b,下列不等式中一定成立的是( )
A、 B、 C、2a>2b D、lg(a-b)>0
6、设A={x||x-2|<3},B={x||x-1|>1},则A∩B等于( )
A、{x| -12}
C、{x| -10时,的方向与的方向 ,当<0时,的方向与的方向 ,当=0时,= ,注意:≠0。
坐标运算:设,则:
①向量的加减法运算: 。
②实数与向量的积: = 。
③若,则,即一个向量的坐标等于表示这个向量的有向线段的终点坐标减去起点坐标。
1、平面向量的数量积:
(1)两个向量的夹角: 当时, ,当时, ,当时, 。
(2)平面向量的数量积:如果两个非零向量,它们的夹角为,我们把数量 叫做的数量积(或内积或点积),记作:,即= ___________。规定: ___,注意数量积是一个 数,不再是一个向量。
④平面向量数量积:。
⑥两点间的距离:若,则。
2、向量平行(共线)的充要条件:
3、向量垂直的充要条件:.
三.基础训练
1.下列四个命题中,正确命题的个数是( )
①共线向量是在同一条直线上的向量 ②若两个向量不相等,则它们的终点不可能是同一点 ③与已知非零向量共线的单位向量是唯一的 ④四边形ABCD是平行四边形的充要条件是与,与分别共线.
2、下列各式或命题中:
① ② ③ ④若两个非零向量、 满足 (k≠0),则、同向. 正确的个数为 ( )
A.0 B.1 C.2 D.3
3、在矩形ABCD中,O为AC中点,若 =3, =2, 则等于 ( )
A.(3+2) B. (3-2) C. (2-3) D. (3+2
4.若,且,则向量与的夹角为( )
(A)30° (B)60° (C)120° (D)150°
5、已知,则向量与向量的夹角是( )
A. B. C. D.
6、已知,向量与垂直,则实数的值为
(A) (B) (C) (D)
7.在△ABC中,∠C=90°,则k的值是 ( )
A.5 B.-5 C. D.
8、若向量=(1,1),=(-1,1),=(4,2),则=( )
A.3+ B. 3- C.-+3 D. +3
9、平面向量与的夹角为,, 则=( )
(A) (B) (C) 4 (D)12
10、已知向量,.若向量满足,,则 ( )
A. B. C. D.
11、已知向量,如果∥,那么
A.且与同向 B.且与反向
C.且与同向 D.且与反向
12、若向量=(3,2),=(0,-1),则2-= ;2·=
13、已知向量=(1,1),=(1,-1),=(-1,2),若=,则=
14、若向量与向量=(1,-2)的夹角是180°,且︱︱=3,则=
15.已知向量和向量的夹角为,,则向量和向量的数量积= 。
16.已知向量,, ,若 则= .
17、已知向量a = (2,1), a·b = 10,︱a + b ︱= ,则︱b ︱=
18.如上图,M、N是△ABC的一边BC上的两个三等分点,
若=a,=b,则=_______.
19、设ABCD是平行四边形,O是对角线AC与BD的交点,且,,则下列命题中正确的
有 (填序号)
① ; ② 当||=||=|-|=1时,|+|=;
③ 当+与-垂直时,则∣∣=∣∣; ④ 当|+|=|-|时,则⊥
20.已知A,B,C是三角形ABC三内角,向量m=(-1,),n=(cosA,sinA),且m·n=1.
(1) 求角A;
(2) 若求tanB。
21.已知向量,,且满足。
(1)求函数的解析式;并求函数的最小正周期和最值及其对应的值;
(2)锐角中,若,且,,求的长.
基础知识专题训练12
一.高考要求
内 容
等级要求
A
B
C
数列
数列的有关概念
√
等差数列
√
等比数列
√
二.基础知识
1、数列的概念:数列是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的特殊函数,数列的 也就是相应函数的解析式。
与的关系:.
2.等差数列与等比数列:
等差数列
等比数列
定义
(,…)
(,…)
通项公式
,
,
求和
公式
中项
公式
对称性
若,则
若,则
分段和原理
、、成等差数列
、、成等比数列
三.基础训练
1.数列1,3,7,15,…的通项公式an 等于( ).
(A)2n (B)2n+1 (C)2n-1 (D)2n-1
2.记数列{an}的前n项和为Sn,且an=6n2+2n-1,则Sn= ( )
A. n2(2n-1) B. n·(6n2+2n-1) C. 2n(n2+2n-1) D. n·(2n2+4n+1)
3.等差数列—3,1,5,…的第15项的值是( )
A.40 B.53 C.63 D.76
4.设是等差数列的前项和,若,则( )
A. B. C. D .
5.在等差数列中,已知则等于( )
A.40 B.42 C.43 D.45
6.已知等差数列的公差为2,若、、成等比数列,则等于( )
A.-4 B.-6 C.-8 D.--10
7.已知是等差数列,,其前10项和,则其公差( )
A. B. C. D.
8.等差数列{an}中,a1=1,a3+a5=14,其前n项和Sn=100,则n=( )
A.9 B.10 C.11 D.12
9.设等差数列的前项和为,若,,则( )
A.63 B.45 C.36 D.27
10.设Sn是等差数列{an}的前n项和,若=,则=( )
A B C D
11.等比数列中, 则的前项和为( )
A. B.
C. D.
12.与,两数的等比中项是( )
A. B. C. D.
13.已知一等比数列的前三项依次为,那么是此数列的第( )项
A. B. C. D.
14.在公比为整数的等比数列中,如果那么该数列的前项之和为( )
A. B.
C. D.
15.已知等差数列的公差为,若成等比数列, 则( )
A. B.
C. D.
16.在等比数列{an}中,a5a7=6,a2+a10=5,则等于( )
A. B. C. D. 或
17.在中,是以为第三项, 为第七项的等差数列的公差,是以为第三项, 为第六项的等比数列的公比,则这个三角形是( )
A.钝角三角形 B.锐角三角形
C.等腰直角三角形 D.以上都不对
18.等差数列中,,则=.
19.已知数列的通项,则其前项和 .
20.已知是等差数列,,其前5项和,则其公差 .
21.已知等差数列的前项和为,若,则 .
22.在等比数列中, 若则��=___________.
23.在等比数列中, 若是方程的两根,则��=___________.
24.在正项等比数列中,,则_______。
25.已知函数,那么
基础知识专题训练17
一、 考试要求
内容
等级要求
A
B
C
统计与统计案例
抽样方法
√
总体分布的估计
√
总体特征数的估计
√
统计案例
√
二、 基础知识
(1)统计
1、 抽样方法:简单随机抽样(抽签法、随机数表法);系统抽样;分层抽样。
注:每个个体被抽到的概率都相等
补:总体——要考察的对象的全体;个体——每一个考察对象;
样本——总体中被抽取的考察对象的集体;样本容量——样本中个体的数目
2、 总体分布的估计:用样本估计总体,是研究统计问题的一个基本思想方法,即用样本平均数估计总体平均数(即总体期望值――描述一个总体的平均水平);用样本方差估计总体方差(方差和标准差是描述一个样本和总体的波动大小的特征数,方差或标准差越小,表示这个样本或总体的波动越小,即越稳定)。一般地,样本容量越大,这种估计就越精确。总体估计要掌握:(1)“表”(频率分布表);(2)“图”(频率分布直方图)。
频率分布表——全距、组距、频数、频率的求法 频率直方图的画法及横纵轴的表示
茎叶图——茎、叶的表示
提醒:直方图的纵轴(小矩形的高)一般是频率除以组距的商(而不是频率),横轴一般是数据的大小,小矩形的面积表示频率。
3、总体特征数的估计:①……的平均数 ;
②设一组数据……,其平均数为,
则其方差 (=); 标准差
③……的平均数为 ;方差为 (用、表示)
④……的平均数为 ;方差为 。
(2)统计案例
1.变量相关关系:当自变量一定时,因变量的取值带有一定的随机性的两个变量之间的关系称为相关关系
回归分析: 对具有相关关系的两个变量进行统计分析的方法叫做回归分析通俗地讲,回归分析是寻找相关关系中非确定性关系的某种确定性.
(1)散点图:(2)回归直线
2. 回归分析
(1)相关系数
当时,表明两个变量正相关;
当时,表明两个变量负相关.
的绝对值越接近于0时,表明两个变量之间几乎不存在线性相关关系.通常大于0.75时,认为两个变量有很强的线性相关性.
(2)相关指数
的值越大,说明残差平方和越小,也就是说模型的拟合效果越好.在线性回归模型中, 表示解释变量对预报变量变化的贡献率, 越接近于1,表示回归的效果越好.
3.独立性检验
(2)列联表:列出两个分类变量的频数表,称为列联表.假设有两个分类变量X和Y,它们的可能取值分别为,其样本频数列联表(称为2×2列联表)为
2×2列联表
总计
总计
构造一个随机变量,其中为样本容量.
附:
二、 基础训练
1.某工厂质检员每隔10分钟从传送带某一位置取一件产品进行检测,这种抽样方法是( )
A.分层抽样 B.简单随机抽样 C.系统抽样 D.以上都不对
2. 某公司在甲、乙、丙、丁四个地区分别有150个,120个,180个,150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务等情况,记这项调查为②;则完成①②这两项调查采用的抽样方法依次是 ( )
A.分层抽样,系统抽样 B.分层抽样,简单随机抽样法
C.系统抽样,分层抽样 D.简单随机抽样法,分层抽样法
3. 某单位有职工100人,不到35岁的有45人,35岁到49岁的有25人,剩下的为50岁以上的人,用分层抽样的方法从中抽取20人,各年龄段分别抽取多少人( )
A.7,5,8 B.9,5,6 C.6,5,9 D.8,5,7
4.某学校为了了解高一年级学生对教师教学的意见,打算从高一年级500名学生中抽取50名进行调查,现将这500名学生按1~500进行编号,并均分为50组,若第4组抽的是34号,第9组抽的是84号,那么第12组应抽几号? ( )
A.102 B.120 C.112 D.114
5. 图1是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
A.65 B.64 C.63 D.62
6.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为a,x4,x5,x6,…,x10的平均数为b,则样本数据的平均数为( )
(A) (B) (C) (D)
7.同一总体的两个样本,甲样本的方差是-1,乙样本的方差是-,则( )
(A)甲的样本容量小 (B)甲的样本平均数小
(C)乙的平均数小 (D)乙的波动较小
8.某校有500名学生参加毕业会考,其中数学成绩在85~100分之间的有共180人,这个分数段的频数是( )
(A)180 (B)0.36 (C)0.18 (D)500
9.某校男子足球队16名队员的年龄如下:
17 17 18 18 16 18 17 15
18 18 17 16 18 17 18 14
这些队员年龄的众数与中位数分别是…………………( )
(A)17岁与18岁 (B)18岁与17岁 (C)17岁与17岁 (D)18岁与18岁
10.下列两个变量之间的关系中,哪个是函数关系 ( )
A.学生的性别与他的数学成绩 B.人的工作环境与健康状况
C.女儿的身高与父亲的身高 D. 正三角形的边长与面积
11、设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x的回归直线的斜率是b,纵截距是a,那么必有( )
(A) b与r的符号相同 (B) a与r的符号相同
(C) b与r的相反 (D) a与r的符号相反
12、一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为y=7.19x+73.93
用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
(A)身高一定是145.83cm (B)身高在145.83cm以上
(C)身高在145.83cm以下 (D)身高在145.83cm左右
13、两个变量与的回归模型中,分别选择了4个不同模型,它们的相关指数如下 ,其中拟合效果最好的模型是( )
(A)模型1的相关指数为0.98 (B) 模型2的相关指数为0.80
(C)模型3的相关指数为0.50 (D) 模型4的相关指数为0.25
14、工人月工资(元)依劳动生产率(千元)变化的回归直线方程为,下列判断正确的是( )
(A)劳动生产率为1000元时,工资为50元
(B)劳动生产率提高1000元时,工资提高150元
(C)劳动生产率提高1000元时,工资提高90元
(D)劳动生产率为1000元时,工资为90元
15.由右表可计算出变量的线性回归方程为( )
5
4
3
2
1
2
1.5
1
1
0.5
A. B.
C. D.
16.若由一个2×2列联表中的数据计算得到χ2=3.528,那么( )
(A)有95%的把握认为这两个变量有关系
(B)有95%的把握认为这两个变量存在因果关系
(C)有99%的把握认为这两个变量有关系
(D)没有充分的证据显示这两个变量之间有关系
17.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
认为作业多
认为作业不多
合计
喜欢玩电脑游戏
18
9
27
不喜欢玩电脑游戏
8
15
23
合计
26
24
50
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( )
(A)99% (B)95% (C)90% (D)无充分依据
18.从含有N个个体的总体中一次性地抽取n个个体,假定其中每个个体被抽取的机会相等,则总体中每个个体被抽取的概率都等于 。
19.把容量是64的样本分成8组,从第1组到第4组的频数分别是5,7,11,13,第5组到第7组的频率是0.125,那么第8组的频数是__________,频率是_______.
20.样本数据-1,2,0,-3,-2,3,1的标准差等于__________.
21、某中学有高一学生400人,高二学生300人,高三学生300人,现通过分层抽样抽取一个容量为n的样本,已知每个学生被抽到的概率为0.2,则n= _______
22、甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如表所示:
甲
乙
丙
丁
8.5
8.8
8.8
8
3.5
3.5
2.1
8.7
则参加奥运会的最佳人选为
23、 某校为了了解学生的体育锻炼情况,随机
调查了70名学生,得到他们在某一天各自的体育锻炼时间的数
据,结果用如图3所示的条形图表示. 根据条形图可得这70名
学生这一天平均每人的体育锻炼时间为 小时.
24、下图是2007年在广州举行的全国少数民族运动会上,七位评委为
某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,
所剩数据的平均数和方差分别为 。
25.为了解某地初三年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高),分组情况如下:
分组
147.5~155.5
155.5~163.5
163.5~171.5
171.5~179.5
频数
6
21
频率
0.1
(1)求出表中a,m的值. (2)画出频率分布直方图和频率折线图
基础知识专题训练18
一、 考试要求
内容
等级要求
A
B
C
概率、统计
随机事件与概率
√
互斥事件及其发生的概率
√
古典概型
几何概型
√
二、基础知识
1、随机事件的概念
在一定的条件下所出现的某种结果叫做事件。
(1)随机事件:在一定条件下可能发生也可能不发生的事件;
(2)必然事件:在一定条件下必然要发生的事件;
(3)不可能事件:在一定条件下不可能发生的事件。
2、随机事件的概率
事件A的概率:在大量重复进行同一试验时,事件A发生的频率总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A)。
由定义可知0≤P(A)≤1,显然必然事件的概率是1,不可能事件的概率是0。
3,互斥事件及对立事件
(1)事件A与B 的两个事件称为互斥事件。
(2)如果事件A、B互斥,那么事件A+B发生的概率P(A+B)=
(3) 对立事件(): 的两个事件。P()=1-P(A)
(4) A,B为对立事件,则A,B为互斥事件;A.B为互斥事件,则A,B不一定为对立事件
4、古典概型
(1)古典概型的两大特点:① ;②
(2)古典概型的概率计算公式:P(A)=
5、古典概型
(1)古典概型的两大特点:① ;②
(2) 几何概型的概率计算公式:P(A)=
三、基础训练
1. 下列事件中,属于随机事件的是( ).
A掷一枚普通正六面体骰子所得的点数不超过6.
B买一张体育彩票中奖.
C太阳从西边落下.
D口袋中装有10个红球,从中摸出一个白球.
2. 从1,2,3,…9这9个自然数中任取两个数,分别有下列事件;(1)恰有一个奇数和恰有一个偶数;(2)至少有一个奇数和两个都是偶数;(3)两个都是奇数和两个都是偶数;(4)至少有一个奇数和至少有一个偶数,其中为互斥事件的是
A (1) B (2)(4) C (2)(3) D (3)
3. 从2件一等品和2件二等品中任取2件,是对立事件的为( )
A 至少有1件二等品与全是二等品 B 至少有1件一等品与至少有1件二等品
C 恰有1件二等品与恰有2件二等品 D 至少有1件二等品与全是一等品
4. 从甲、乙、丙三人中任选两名代表,甲被选中的概率为( )
A. B. C. D. 1
5.一枚硬币连掷3次,只有一次出现正面的概率是 ( )
A. B. C. D.
6 从分别写有A、B、C、D、E的5张卡片中,任取2张,这2张卡片上的字母恰好是按字母顺序相邻的概率为
A. B. C. D.
7. 某小组共有5名学生,其中女生2名,现选举2名代表,至少有1名女生当选的概率为
A. B. C. D.1
8 取一根长度为3 m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1 m的概率是.
A. B. C. D.不确定
9. 在1万 km2的海域中有40 km2的大陆架贮藏着石油,假如在海域中任意一点钻探,钻到油层面的概率是.
A. B. C. D.
10.某射手在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21,0.23,0.25,0.28,计算这个射手在一次射击中:射中10环或7环的概率是_______
11、在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同。现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是
12、先后抛掷两枚均匀的正方体骰子,骰子朝上的点数分别为、,则的概率为________
13.如图,一颗豆子随机扔到桌面上,假设豆子不落在线上,
则它落在阴影区域的概率为________.
14、向圆所围成的区域内随机地丢一粒豆子,则豆子落在直线上方的概率是_____________.
15、一个袋子中装有分别标注数字1,2,3,4的四个小球,这些小球除标注的数字外完全相同。从中随机取出2个小球,每个小球被取出的可能性相等。
(1)若不放回抽取,求取出的两个球的标号至少有一个大于2的概率;
(2)若放回抽取,求取出的两个球的标号恰好相同的概率。
16.已知向量,.
(Ⅰ)若,分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足的概率;
(Ⅱ)若,求满足的概率.
基础知识专题训练19
一、考试要求
内容
等级要求
A
B
C
空间几何体
柱、锥、台、球及其简单组合体
√
三视图与直视图
√
柱、锥、台、球的表面积和体积
√
二、基础知识
1.空间几何体
棱柱:侧棱都平行且相等,上下底面是全等的多边形,并且相
互平行
(1).多面体 棱锥:底面是任意多边形。侧面是有一个公共顶点的三角形
棱台:由平行于底面的平面截棱锥得到,上下底面是相似多边形
(2).旋转体
三.基础练习
1.若圆锥的高扩大到原来的2倍,底面半径缩短到原来的,则圆锥的体积( ).
A.缩小到原来的一半 B.扩大到原来的2倍
C.不变 D.缩小到原来的
解析 设原圆锥的高为h,底面半径为r,体积为V,则V=r2·h;变化后圆锥的体积V′=×2×2h=πr2·h=V.
答案 A
2.在长方体ABCD-A1B1C1D1截去一角B1-A1BC1,则它的体积是长方体体积的
( ).
A. B. C. D.
解析 =· =
× ×B1C1=
3.若顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
( ).
A.16π B.20π C.24π D.32π
4
.若圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( ).
A.7 B.6 C.5 D.3
解析 设较小底面半径为r,另一底面半径为R,则2πR=3×2πr,∴R=3r.
由侧面积公式得π(r+3r)l=84π,
即π(r+3r)·3=84π.∴r=7.
答案 A
5.(2012·汕头一检)如右图,在长方体ABCDA1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC,A1D1的两个平行截面将长方体分成三部分,其体积分别记为V1= ,V3= ,其余部分为V2,若V1∶V2∶V3=1∶4∶1,则截面A1EFD1的面积为( ).
A.4 B.8 C.4 D.16
解析 三部分都是棱柱,三棱柱AA1EDD1F,三棱柱B1BE1C1CF1和四棱柱A1EBE1D1FCF1,显然它们等高,设为h,
由V1∶V2∶V3=1∶4∶1
得S1h∶S2h∶S3h=1∶4∶1.
∴S1∶S2∶S3=1∶4∶1
设AE=a,则BE=6-a,
∴(6-a)×3=4××a×3,∴a=2.
∴A1E==.
答案 C
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中的横线上)
6.底面直径和高都是4 cm的圆柱的侧面积为________cm2.
解析 圆柱的底面半径为r=×4=2,∴S侧=2π×2×4=16π
答案 16π
7.若一个长方体的正视图、侧视图、俯视图的面积分别为4 cm2,6 cm2,24 cm2,则该长方体的体积等于________.
解析 设长方体的长、宽、高分别为a、b、c,则有ab=24,ac=4,bc=6,
所以(abc)2=24×6×4,
所以abc=24(cm3),即长方体的体积为24 cm3.
8.如图所示,扇形所含的中心角为90°,弦AB将扇形分成两个部分,这两部
分各以AO为轴旋转一周,所得的旋转体体积V1和V2之比为________.
解析 Rt△AOB绕OA旋转一周形成圆锥,其体积V1=R3,
扇形绕OA旋转一周形成半球面,
其围成的半球的体积V=R3,
∴V2=V-V1=R3-R3=R3.
∴V1∶V2=1∶1.
答案 1∶1
15.(10分)圆柱的高是8 cm,表面积是130 π cm2,求它的底面圆半径和体积.
解 设圆柱的底面圆半径为r cm,
∴S圆柱表=2π·r·8+2πr2=130π.
∴r=5(cm),即圆柱的底面圆半径为5 cm.
则圆柱的体积V=πr2h=π×52×8=200π(cm3).
16.(10分)如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
解 以AD为旋转轴,DC、CB、BA为母线旋转一周形成的图形是一个圆台上方挖去一个圆锥后形成的几何体.
S表面=S圆台底面+S圆台侧面+S圆锥侧面=π×52+π×(2+5)×5+π×2×2=(70+4)π;
V=V圆台-V圆锥=π(r+r1r2+r)h-πrh1=π.
18.(12分)已知正三棱锥S-ABC,一个正三棱柱的一个底面的三个顶点在正三棱锥的三条侧棱上,另一底面在正三棱锥的底面上,若正三棱锥的高为15 cm,底面边长为12 cm,内接正三棱柱的侧面积为120 cm2.
(1)求三棱柱的高;
(2)求棱柱上底面截棱锥所得的小棱锥与原棱锥的侧面积之比.
解 (1)设正三棱柱高为h,底面边长为x,如图,则=,
∴x=(15-h).①
又S三棱柱侧=3x·h=120,
∴xh=40.②
解①②得或
故正三棱柱的高为10 cm或5 cm.
(2)由棱锥的性质,得 =2=或
=2=.
19.(12分)如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求:
(1)绳子的最短长度的平方f(x);
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.
解 将圆锥的侧面沿SA展开在平面上,如图,则该展开图为扇形,且弧AA′的长度L就是⊙O的周长,
∴L=2πr=2π.
∴∠ASA′=×360°=×360°=90°,
(1)由题意知,绳长的最小值为展开图中的AM,其值为
AM=(0≤x≤4),
∴f(x)=AM2=x2+16(0≤x≤4).
(2)绳子最短时,在展开图中作SR⊥AM,垂足为R,
则SR的长度为顶点S到绳子的最短距离.
在△SAM中,∵S△SAM=SA·SM=AM· SR,
∴SR==(0≤x≤4).
(3)∵f(x)=x2+16(0≤x≤4)是增函数,
∴f(x)的最大值为f(4)=32.
基础知识专题训练20
一、考试要求
内 容
等级要求
A
B
C
点、线、面之间的位置关系
平面及其基本性质
√
直线与平面平行、垂直的判定与性质
√
二、基础知识
1.平面概述
(1)平面的特征:①无限延展 ②没有厚度
(2)平面的画法:通常画__________来表示平面;
(3)平面的表示:用一个小写的希腊字母、、等表示,如平面、平面;用表示平行四边形的两个相对顶点的字母表示,如平面AC。
2.三公理三推论:
公理1:______________________________________________________
公理2:______________________________________________________
公理3:______________________________________________________
推论一:______________________________________________________
推论二:______________________________________________________
推论三:______________________________________________________
3.空间直线:
(1)空间两条直线的位置关系:
相交直线——有且仅有一个公共点;
平行直线——在同一平面内,没有公共点;
异面直线——_____________________________。相交直线和平行直线也称为____直线。
(2)公理4:____________________________________
4.直线和平面的位置关系
(1)直线在平面内(无数个公共点),符号:_______;
(2)直线和平面相交(有且只有一个公共点),符号:________;
(3)直线和平面平行(没有公共点),符号:__________。
5. 平面与平面位置关系。
(1)平面和平面相交(无数个公共点),符号:________;
(2)平面和平面平行(没有公共点),符号:__________。
三、基础训练
1.下列命题错误的是( )
A.平面和平面相交,它们只有有限个公共点
B.经过一条直线和这条直线外的一点,有且只有一个平面
C.经过两条相交直线,有且只有一个平面
D.如果两个平面有三个不共线的公共点,那么这两个平面重合
2.若直线a不平行于平面,且a内,则下列结论成立的是( )
A. 内的所有直线与a异面
B. 内不存在与a平行的直线
C. 内存在唯一的直线与a平行
D. 内的直线与a都相交
3.下列命题中正确的个数是( )
(1)若直线上有无数个点不在平面内,则//
(2)若直线与平面平行,则与平面内任一条直线都平行
(3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
(4)若//,则与平面内的任一条直线都没有公共点
A.0 B.1 C.2 D.3
4.给定空间中的直线及平面a,条件“直线L与平面a内无数条直线都垂直”是“直线与平面a垂直”的( )条件
A.充要 B.充分非必要 C.必要非充分 D.既非充分又非必要
5.设是两条直线,是两个平面,则能得到的一个条件是( )
A. B.
C. D.
6.已知是两条不同直线,是三个不同平面,下列命题中正确的是( )
A. B.
C. D.
7.已知直线及平面,下列命题中的假命题是 ( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
8.已知直线是异面直线,直线分别与都相交,则直线的位置关系
A.可能是平行直线 B.一定是异面直线
C.可能是相交直线 D.平行、相交、异面直线都有可能
9.已知两条直线,两个平面,给出下面四个命题:[来源:学_科_网]
① ②[来源:学科网ZXX]
③ ④
其中正确命题的序号是( )
A.①③ B.②④ C.①④ D.②③
10.已知是平面,是直线,则下列命题中不正确的是
A.若∥,则 B.若∥,则∥
C.若,则∥ D.若,则
11. 设表示平面,表示直线,给定下列四个命题:
①;②;
③;④.其中正确命题的个数有2个
12.已知是不重合的直线,是不重合的平面,有下列命题:①若,则;②若,,则;③若,,则;④若,则.其中真命题有 .(写出所有真命题的序号)
13.在正三棱锥P-ABC中,D,E分别是AB,BC的中点,有下列三个结论:
① AC⊥PB; ② AC∥平面PDE;③ AB⊥平面PDE。则所有正确结论的序号是 。
14.如图所示,正方体ABCD—A1B1C1D1中,
则EF和BD1的关系是
基础知识专题训练21
一、考试要求
内 容
等级要求
A
B
C
点、线、面之间的位置关系
平面及其基本性质
√
直线与平面平行、垂直的判定与性质
√
两平面平行、垂直的判定与性质
√
二、基础知识
1.直线与平面平行的判定定理:___________________________________________________,
符号语言:_________________________________________.
直线与平面平行的性质定理:________________________________________________________,
符号语言:________________________________________.
2.两个平面平行的判定定理:________________________________________________
符号语言:_________________________________________________
两个平面平行的性质定理
(1)__________________________________________________________;
符号语言:________________________________________.
(2)__________________________________________________________。
符号语言:________________________________________.
3.线面垂直定义:__________________________________________________________
符号语言:_________________________________________
直线与平面垂直的判定定理:_______________________________________________,
符号语言:_________________________________________.
直线和平面垂直的性质定理:_______________________________________________,
符号语言:_________________________________________.
4.两个平面垂直的定义:_____________________________________________________。
两平面垂直的判定定理:_______________________________________________________。
符号语言:_________________________________________.
两平面垂直的性质定理:_______________________________________________________.。
符号语言:_________________________________________.
三、基础训练
1.已知直线及平面,下列命题中的假命题是 ( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
2.如图,四棱锥P—ABCD的底面ABCD是一个正方形,PD垂直
于ABCD,则这个四棱锥的五个面中,互相垂直的平面共有( )
A.3对 B.4对 C.5对 D.6对
3. 若表示直线,表示平面,则下列命题中,正确命题的个数为( )
①; ②;
③; ④
A.1个 B.2个 C.3个 D.4个
4. 在正四面体中,分别是的中点,下面四个结论中不成立的是( )
A. B.
C. D.
5、下列四个正方体图形中,为正方体的两个顶点,分别为其所在棱的中点,能得出平面的图形的序号是__________
6. 已知平面,和直线a,b,c,且a∥b∥c,a,b,c则与的关系是__________.
7.已知平面和直线,给出条件:①;②;③;④;⑤.
当满足条件 时,有。(填所选条件的序号)
8、若是两个不重合的平面,以下条件中可以判断∥的是:_______:
①都垂直于平面;②内有不共线的三点到的距离相等;
③是内的两条直线,且∥,∥;
④是两条异面直线,且∥,∥,∥,∥.
9.已知三条不重合的直线m、n、l,两个不重合的平面,有下列命题
①若; ②若;
③若; ④若;
其中正确的命题个数是_______
10.关于直线,与平面,,有以下四个命题,其中真命题的序号是_________:
①若且,则; ②若且,则;
③若且,则; ④若且,则.
11.如图,AB是⊙的直径,PA垂直于⊙所在的平面,C是圆周上不同于A,B的任意一点,
(1)求证:BC⊥平面PAC
(2)求证:平面PAC⊥平面PBC;
12. 如图,在底面为平行四边形的四棱锥中,,,且,点是的中点.
(1)求证:;
(2)求证:∥平面.
13. 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点.
(1)求证:AF∥平面PCE;
(2)求三棱锥C-BEP的体积.
14.如图所示, 四棱锥PABCD底面是直角梯形, 底面ABCD, E为PC的中点, PA=AD=AB=1.
(1)证明: ;
(2)证明: ;
(3)求三棱锥BPDC的体积V.
15、已知:正方体,,E为棱的中点.
(Ⅰ) 求证:;
(Ⅱ) 求证:平面;
(Ⅲ)求三棱锥的体积.
16、如图,己知中,,,且
(1)求证:不论为何值,总有
(2)若求三棱锥的体积.
基础知识专题训练22
一、考试要求
内 容
等级要求
A
B
C
平面解析几何初步
直线的斜率和倾斜角
√
直线方程
√
直线的平行关系与垂直关系
√
二、基础知识
1.倾斜角:一条直线L向上的方向与X轴的________所成的_______,叫做直线的倾斜角,范围为________。
2.斜率:(1)当直线的倾斜角不是___时,则称其正切值为该直线的斜率,即k=______;当直线的倾斜角等于900时,直线的斜率_______。
(2)过两点p1(x1,y1),p2(x2,y2)(x1≠x2)的直线的斜率公式:k=___________
(若x1=x2,则直线p1p2的斜率不存在,此时直线的倾斜角为900)。
3.直线方程的五种形式
名称
方程
说明
适用条件
斜截式
k——斜率
b——纵截距
倾斜角为90°的直线不能用此式
点斜式
(x0,y0)——直线上
已知点,k——斜率
倾斜角为90°的直线不能用此式
两点式
(x1,y1),(x2,y2)是直线上两个已知点
与两坐标轴平行的直线不能用此式
截距式
a——直线的横截距
b——直线的纵截距
过(0,0)及与两坐标轴平行的直线不能用此式
一般式
,,分别为斜率、横截距和纵截距
A、B不能同时为零
直线的点斜式与斜截式不能表示斜率不存在(垂直于x 轴)的直线;两点式不能表示平行或重合两坐标轴的直线;截距式不能表示平行或重合两坐标轴的直线及过原点的直线。
4.两条直线的位置关系:
直线方程
平行的充要条件
垂直的充要条件
备注
有斜率
不可写成分式
5.距离公式
1.两点间距离:若,则
特别地:轴,则、轴,则。
2.点到直线的距离:,则P到l的距离为:
3.平行线间距离:若,
则:。注意点:x,y对应项系数应相等。
三、基础训练
1.直线的倾斜角为,斜率为,直线过点,,斜率为,则 ( )
A B C D 不能确定
2.过点且与直线平行的直线的方程是( )
A. B.
C. D.
3. 已知是第二象限角,直线不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.直线过点 (-3,-2)且在两坐标轴上的截距相等,则这直线方程为 ( )
A. B.
C. 或 D. 或x-y+5=0
6. 直线与直线平行,则的值为( )
A.2 B.-3 C.2或-3 D.-2或-3
7.若直线与垂直,则等于
A.5 B.-3 C.5或-3 D不存在
8.已知点,则直线的倾斜角是_________
9.直线经过点,且与两坐标轴围成一个等腰直角三角形,直线的方程_________
10.已知直线过点,且与轴、轴的正半轴分别交于、两点,为坐标原点,则△OAB面积的最小值为 .
11. 已知关于直线的对称点为,则直线的方程是__________________
12. 已知点,在直线上求一点P,使最小.
13.与直线平行,且距离等于的直线方程是 .
14.已知直线与圆相切,则的值为 .
15.若直线mx+y+2=0与线段AB有交点,其中A(-2, 3),B(3,2),则实数m的取值范围是
_____________.
基础知识专题训练23
一、考试要求
内 容
等级要求
A
B
C
平面解析几何初步
圆的标准方程和一般方程
√
直线与圆、圆与圆的位置关系
√
空间直角坐标系
√
二、基础知识
1.圆的方程
(1)圆的标准方程:_______________________。圆心为_________,半径为________
(2)圆的一般方程________________________,圆心为点_______,半径_________________。
注:二元二次方程,表示圆的方程的充要条件是:
_________________________。
注:求圆的方程常用的方法:待定系数法(标准方程或一般方程);数形结合求圆心、半径
2.直线与圆的位置关系有三种():
(1)若;(2);(3)。
注:还可以利用直线方程与圆的方程联立方程组求解,通过解的个数来判断.
直线与圆相交的弦长公式: ①几何方法:;
②代数方法:
3.两圆位置关系的判定方法:设两圆圆心分别为O1,O2,半径分别为r1,r2,。
; ;
; ;
;
判断两个圆的位置关系也可以通过联立方程组判断公共解的个数来解决。
4.点和圆的位置关系的判别转化为点到圆心的距离与半径的大小关系。
点,圆的方程:
如果 _____点在圆外;
如果______点在圆内;
如果______点在圆上。
三、基础训练
1.圆的圆心坐标和半径分别为
A. , 6 B. , 6 C. , 36 D , 36
2斜率为1,与圆相切的直线的方程为 ( )
A. B.
C.或 D. 或
3.过圆上一点作圆的切线,则切线方程为
A. B. C. D.
4..圆和圆的位置关系是 ( )
相离 相交 外切 内切
5.直线被圆截得的弦长为 ( )
A. B.2 C.3 D.4
6.已知点在圆外,则
A. B. C. 或 D.不能确定
7.方程表示一个圆,则的取值范围是
A B C D
8.过三点, , 的圆的方程为
A. B.
C. D.
9.过坐标原点且与圆相切的直线的方程为_________________
10.直线截圆得的劣弧所对的圆心角为_______________
11.设直线与圆相交于、两点,且弦的长为,则 .
12.直线与圆没有公共点,则的取值范围是__________
13.若直线与圆有两个不同的交点,则的取值范围是 .
14.圆和圆的位置关系是______________________
15.圆上的点到直线的最大距离与最小距离的差是___________
基础知识专题训练24
一、考试要求
内 容
等级要求
A
B
C
圆锥曲线与方程
椭圆的标准方程和几何性质
√
双曲线的标准方程和几何性质
√
抛物线的标准方程和几何性质
√
二、基础知识
1.椭圆与双曲线的性质:
椭 圆
双 曲 线
定义
方程
图形
M2
M11
P
K2
K1
A1
A2
F2
F1
O
y
x
焦点
焦距
范围
-a≤x≤a,-b≤y≤b
-b≤x≤b,-a≤y≤a
x≥a或x≤-a,
y≥b或y≤-b
y≥a或y≤-a,
x≥b或x≤-b
对称轴
关于x、y轴对称,关于原点成中心对称
顶点
长轴:(-a,0),(a,0)
短轴:(0,-b),(0,b)
长轴:(-b,0),(b,0)
短轴:(0,-a),(0,a)
实轴:(-a,0),(a,0)
虚轴:(0,-b),(0,b)
实轴:(-b,0),(b,0)
虚轴:(0,-a),(0,a)
轴
长轴长2a,短轴长2b
实轴长2a,虚轴长2b
离心率
准线
渐进线
无
a,b,c
2.抛物线的性质
标准方程
图形
焦点坐标
准线方程
范围
对称性
轴
轴
轴
轴
顶点
离心率
三、基础训练
1.椭圆的离心率为
2 4
2.若抛物线的焦点与椭圆的右焦点重合,则的值为
3. 抛物线的准线方程是
4.已知双曲线,则其渐近线方程为
A B C D
5. 曲线与曲线的关系是
A 焦距相等 B 离心率相等 C焦点相同 D有相等的长、短轴
6.抛物线y=4上的一点M到焦点的距离为1,则点M的纵坐标是
A B C D 0
7.已知△ABC的顶点B、C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是
A 2 B 6 C 4 D 12
8.双曲线的虚轴长是实轴长的2倍,则
A B C D
9.过抛物线 y2 = 4x 的焦点作直线交抛物线于A(x1, y1)B(x2, y2)两点,如果=6,那么=
6 8 9 10
10.已知是椭圆的两个交点,过且与椭圆长轴垂直的直线交椭圆于A、B两点,若 是正三角形,则此椭圆的离心率是
11.已知椭圆中心在原点,一个焦点为F(-2,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
12. 若方程表示的图形是双曲线,则的取值范围为 .。
13.顶点在原点,准线方程为的抛物线方程是 。
14.已知为椭圆的两个焦点,过的直线交椭圆于A、B两点若,则=______________。
15.双曲线的离心率等于,且与椭圆有公共焦点,则该双曲线的方程______
16.若该抛物线上的点到焦点的距离是4,则点的坐标为_____
17.已知椭圆的长轴长是2,焦点坐标分别是(,0),(,0).
(1)求这个椭圆的标准方程;
(2)如果直线与这个椭圆交于两不同的点,求m的取值范围.
18.直线与抛物线相交与A,B两点.求证: