2019届高考数学一轮复习 第15讲 任意角，弧度制，及任意角三角函数学案（无答案）文

2019届高考数学一轮复习 第15讲 任意角，弧度制，及任意角三角函数学案（无答案）文

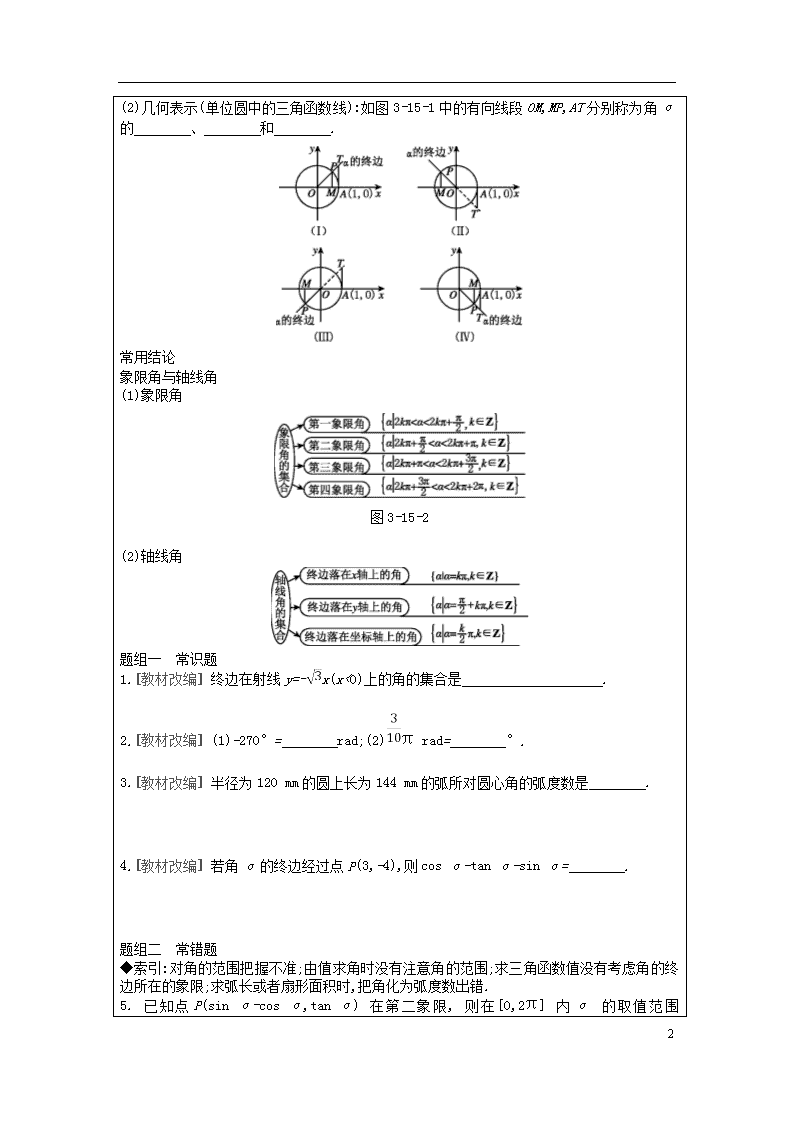
第15讲 任意角，弧度制及任意角的三角函数 考试 说明 ‎1.了解任意角的概念和弧度制的概念. ‎ ‎2.能进行弧度与角度的互化. ‎ ‎3.理解任意角三角函数(正弦、余弦、正切)的定义 考情 分析 考点 考查方向 考例 角的概念 角的概念、角 的集合表示 三角函数的定义 单位圆、三角函 数线、三角函 数值的符号 扇形的弧长及面积公式 扇形弧长、‎ 面积公式 ‎【重温教材】必修4 第一章 第一节，第二节 ‎【相关知识点回顾】‎ ‎1.角的概念的推广 ‎(1)定义:角可以看成平面内的一条射线绕着　　　　从一个位置旋转到另一个位置所形成的图形.  ‎ ‎(2)分类:按旋转方向分为　　　　、　　　　和零角;按终边位置分为　　　　和轴线角. ‎ ‎(3)终边相同的角:所有与角α终边相同的角,连同角α在内,构成的角的集合是S=　　　　　　　　　.  ‎ ‎2.弧度制的定义和公式 ‎(1)定义:把长度等于　　　　的弧所对的圆心角叫作1弧度的角.弧度记作rad. ‎ ‎(2)公式:‎ 角α的弧度的绝对值 ‎|α|=(弧长用l表示)‎ 角度与弧度的换算 ‎①1°= rad,②1 rad=°‎ 弧长公式 弧长l=　　　 ‎ 扇形面积公式 S=lr=|α|r2‎ ‎3.任意角的三角函数 ‎(1)定义:设α是一个任意角,它的终边与单位圆交于点P(x,y),则sin α=　　　　,‎ cos α=　　　　,tan α=(x≠0). ‎ 5‎ ‎(2)几何表示(单位圆中的三角函数线):如图‎3-15-1‎中的有向线段OM,MP,AT分别称为角α的　　　　、　　　　和　　　　. ‎ 常用结论 象限角与轴线角 ‎(1)象限角 图‎3-15-2‎ ‎(2)轴线角 题组一　常识题 ‎1.[教材改编] 终边在射线y=-x(x<0)上的角的集合是　　　　　　　　　　. ‎ ‎2.[教材改编] (1)-270°=　　　　rad;(2)π rad=　　　　°. ‎ ‎3.[教材改编] 半径为‎120 mm的圆上长为‎144 mm的弧所对圆心角的弧度数是　　　　. ‎ ‎4.[教材改编] 若角α的终边经过点P(3,-4),则cos α-tan α-sin α=　　　　. ‎ 题组二　常错题 ‎◆索引:对角的范围把握不准;由值求角时没有注意角的范围;求三角函数值没有考虑角的终边所在的象限;求弧长或者扇形面积时,把角化为弧度数出错.‎ ‎5.已知点P(sin α-cos α,tan α)在第二象限,则在[0,2π]内α 5‎ 的取值范围是　　　　　　　. ‎ ‎6.已知角α的终边落在直线y=-3x上,则-=　　　　. ‎ ‎7.已知角θ的顶点为坐标原点O,始边为x轴的正半轴,若P(x,6)是角θ终边上一点,且cos θ=-,则x=　　　　. ‎ ‎8.若一扇形的圆心角为72°,半径为‎20 cm,则扇形的面积为　　　　cm2. ‎ ‎【探究点一】角的集合表示及象限角的判定 ‎〖典例解析〗‎ 例1.  (1)设集合M=xx=·180°+45°,k∈Z,N=xx=·180°+45°,k∈Z,那么 (　　)‎ A. M=N B. M⊆N C. N⊆M D. M∩N=⌀‎ ‎(2)已知角α的终边在如图所示的阴影区域内(包括边界),则角α用集合可表示为　　　　　　　　. ‎ ‎〖课堂检测〗‎ ‎1.. (1)已知角α,β的终边关于直线x+y=0对称,且α=-60°,则β=　　　　　　　. ‎ ‎(2)若角θ的终边与角的终边相同,则在[0,2π]内终边与角的终边相同的角的个数为　　　　. ‎ ‎[总结反思] ‎ ‎(1)利用终边相同的角的集合可以求适合某些条件的角,方法是先写出与这个角的 5‎ 终边相同的所有角的集合,然后通过对集合中的参数k赋值来求得所需的角;‎ ‎(2)利用终边相同的角的集合S={β|β=2kπ+α,k∈Z}判断一个角β所在的象限时,只需把这个角写成[0,2π)范围内的一个角α与2π的整数倍的和,然后判断角α所在的象限.‎ ‎【探究点二】扇形的弧长、面积公式 ‎〖典例解析〗‎ 例2.(1)若圆弧长度等于该圆内接等腰直角三角形的周长,则其圆心角的弧度数是　　　　. ‎ ‎(2)若扇形的周长为18,则扇形面积取得最大值时,扇形圆心角的弧度数是　　　　. ‎ ‎〖课堂检测〗‎ ‎2.(1)将表的分针拨快10分钟,则分针旋转过程中形成的角的弧度数是 (　　)‎ A. B. C. - D. -‎ ‎(2)圆内接矩形的长宽之比为2∶1,若该圆上一段圆弧的长等于其内接矩形的宽,则该圆弧所对圆心角的弧度数为　　　　. ‎ ‎ [总结反思] ‎ 应用弧度制解决问题的方法:‎ ‎(1)利用扇形的弧长和面积公式解题时,要注意角的单位必须是弧度;‎ ‎(2)求扇形面积最大值的问题时,常转化为二次函数的最值问题,利用配方法使问题得到解决;‎ ‎(3)在解决弧长问题和扇形面积问题时,要合理地利用圆心角所在的三角形 ‎【探究点三】　三角函数的定义 考向1　三角函数定义的应用 ‎ 例3 (1)若角θ的终边经过点P(-,m)(m≠0)且sin θ=,则cos θ=　　　　. ‎ ‎(2)已知角α的终边上一点P的坐标为,若α∈(-π,0),则α=　　　　‎ ‎〖课堂检测〗‎ ‎3.点P从点出发,沿单位圆按逆时针方向运动弧长后到达Q点,若α的始边在x轴正半轴上,终边在射线OQ上,则sin α= (　　)‎ 5‎ A. 1 B. ‎-1 ‎C. D. -‎ ‎[总结反思] 定义法求三角函数值的两种情况:‎ ‎(1)已知角的终边上一点P的坐标,则可先求出点P到原点的距离,然后用三角函数定义求解;‎ ‎(2)已知角的终边所在的直线方程,则可先设出终边上一点的坐标,求出此点到原点的距离,然后用三角函数的定义来求相关问题.‎ 若直线的倾斜角为特殊角,则可直接写出角的三角函数值.注:若角α的终边落在某条直线上,一般要分类讨论.‎ 考向2　三角函数值的符号判定 例4.（1）若sin αcos α>0,且<0,则角α是 (　　)‎ A. 第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角 ‎(2)已知角α的终边经过点(‎3a-6,a+1),且cos α≤0,sin α>0,则实数a的取值范围是 (　　)‎ A. (-1,2] B. (-1,2) C. [-1,2) D. [-1,2]‎ ‎〖课堂检测〗‎ ‎4.角α的终边在第一象限,点P(1‎-2a,2+‎3a)是其终边上的一点,若cos α>sin α,则实数a的取值范围是　　　　. ‎ ‎[总结反思] 三角函数在各象限的符号可用一个口诀记忆:一全正,二正弦,三正切,四余弦.如果角不能确定所在象限,就要进行分类讨论.‎ 考向3　三角函数线的应用 例5.函数y=lg(2sin x-1)+的定义域为　　　　　　　　　　. ‎ ‎〖课堂检测〗‎ ‎5.满足cos α≤-的角α的集合为 　　 　. ‎ ‎[总结反思] ‎ 利用三角函数线解三角不等式,通常采用数形结合的方法,一般来说sin x≥b,cos x≥a,只需作直线y=b,x=a 5‎ 与单位圆相交,分别连接交点与原点即得角的终边所在的位置,此时再根据方向即可确定相应的x的范围 ‎1.[2014·全国卷Ⅰ]若tan α>0,则 (　　)‎ A.sinα>0 B.cosα>‎0 C.sin 2α>0 D.cos 2α>0‎ ‎2.[2017·全国卷Ⅰ]已知α∈,tan α=2,则cosα-=　　　　‎ ‎3.[2017·北京卷]在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sin α=,则sin β=　　　　. ‎ 5‎