史上最难的全国高考理科数学试卷

史上最难的全国高考理科数学试卷

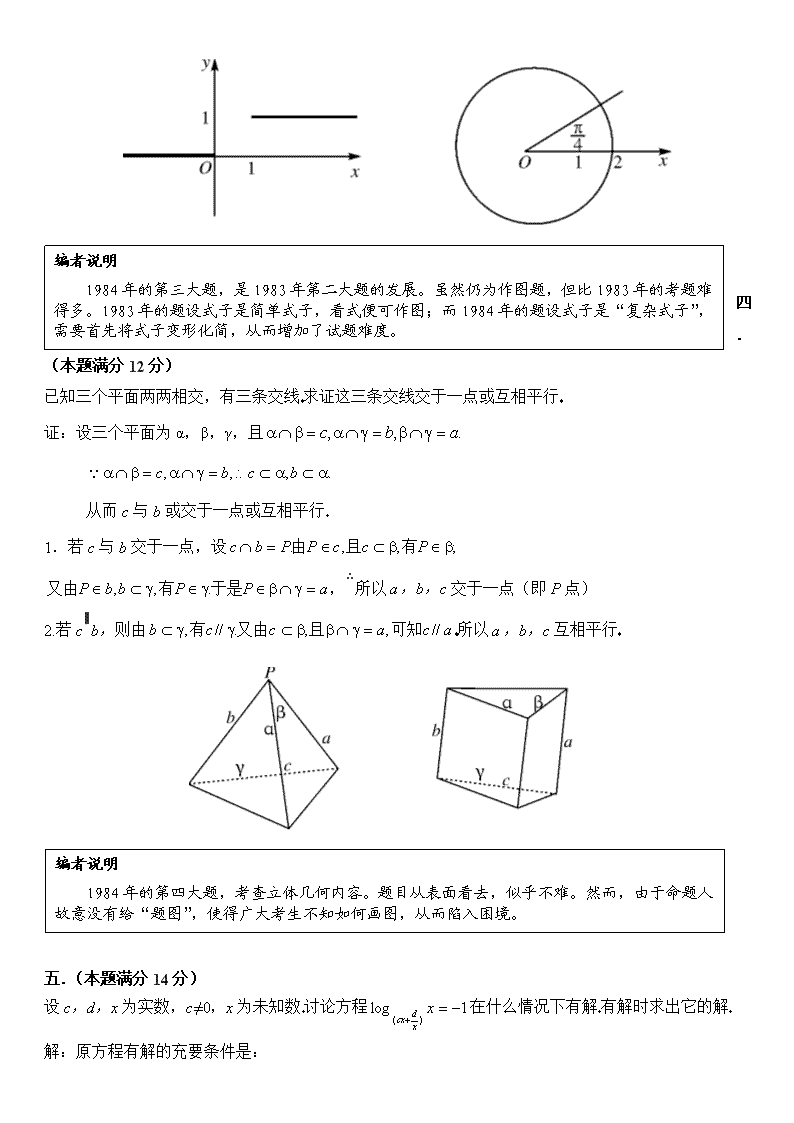
数学月刊七月号 创难度之最的1984年普通高等学校招生全国统一考试理科数学试题 ‎ ‎编者说明 ‎1984年，是中国高考改革有创意的一年。就在这一年，数学命题组提出了高考“出活题，考基础，考能力”的命题指导思想。自1977年恢复高考以来，高考命题基本上是“模仿命题”，模仿课本上的例习题，模仿教参上的参考题，考场上出现了“解题有套”的现象，高校传出了“高分低能”的说法。‎ ‎1984年的数学试卷，创造了大批新题，即所谓活题。广大考生第一次见到这样的新题或活题，感到非常之难。当年，北京市的分数，人均只有17分，创下了新中国成立以来，数学高考难度之“最”。‎ ‎（这份试题共八道大题，满分120分 第九题是附加题，满分10分，不计入总分）‎ 一．（本题满分15分）本题共有5小题，每小题选对的得3分;不选，选错或多选得负1分 ‎1．数集X = {（2n+1）π，n是整数}与数集Y = {（4k1）π，k是整数}之间的关系是 （ C ）‎ ‎（A）XY （B）XY （C）X=Y （D）X≠Y ‎2．如果圆x2+y2+Gx+Ey+F=0与x轴相切于原点，那么（ C ）‎ ‎（A）F=0，G≠0，E≠0. （B）E=0，F=0，G≠0.‎ ‎（C）G=0，F=0，E≠0. （D）G=0，E=0，F≠0.‎ ‎3.如果n是正整数，那么的值 （ B ）‎ ‎（A）一定是零 （B）一定是偶数 ‎（C）是整数但不一定是偶数 （D）不一定是整数 ‎4.大于的充分条件是 （ A ）‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎5．如果θ是第二象限角，且满足那么 （ B ）‎ ‎（A）是第一象限角 （B）是第三象限角 ‎ ‎（C）可能是第一象限角，也可能是第三象限角 （D）是第二象限角编者说明 数学试题选择题，同上一年，即1983年一样多，也是5道小题，但考生感到比上年难得多。有的考生拿到第1小题就不能动笔。‎ 首先是因为1984年对选择题的考题要求很严。第一次也是唯一一次提出“得负分”的评分要求。‎ 第二是选择题的设计，命题人第一次考虑到选择题“淘汰法”解题方法。比如第1小题，排除3个错误答案比选择1个正确答案要迅速得多。可是，在刚刚出现选择题（1983年第一次用选择题）的考场上，考生几乎没有这种解题思想。许多交白卷的考生，首先就被第1题挡住了“去路”。‎ 二．（本题满分24分）本题共6小题，每一个小题满分4分只要求直接写出结果）‎ ‎1．已知圆柱的侧面展开图是边长为2与4的矩形，求圆柱的体积 答：‎ ‎2.函数在什么区间上是增函数？‎ 答：x＜-2.‎ ‎3．求方程的解集 答：‎ ‎4．求的展开式中的常数项 答：-20‎ ‎5．求的值 答：0‎ ‎6．要排一张有6个歌唱节目和4个舞蹈节目的演出节目单，任何两个舞蹈节目不得相邻，问有多少种不同的排法（只要求写出式子，不必计算）‎ 答：‎ 编者说明 ‎1984年的第二大题，含6个小题，比1983年的2个小题多出了4个，从而使整个试卷的题量比1983年多出了3道。题目很活，题量又大，多数考生在规定的时间不能完成解答，这也是1984年数学得分很低的原因之一。‎ 三．（本题满分12分）本题只要求画出图形 ‎1．设画出函数y=H(x-1)的图象 ‎2．画出极坐标方程的曲线 解（1） （2）‎ ‎1. 2.‎ 解：‎ 编者说明 ‎1984年的第三大题，是1983年第二大题的发展。虽然仍为作图题，但比1983年的考题难得多。1983年的题设式子是简单式子，看式便可作图；而1984年的题设式子是“复杂式子”，需要首先将式子变形化简，从而增加了试题难度。‎ 四．（本题满分12分）‎ 已知三个平面两两相交，有三条交线求证这三条交线交于一点或互相平行 证：设三个平面为α，β，γ，且 从而c与b或交于一点或互相平行 ‎1．若c与b交于一点，设 ‎，∴所以，b，c交于一点（即P点）‎ ‎2.若c∥b，则由所以，b，c互相平行 编者说明 ‎1984年的第四大题，考查立体几何内容。题目从表面看去，似乎不难。然而，由于命题人故意没有给“题图”，使得广大考生不知如何画图，从而陷入困境。‎ 五．（本题满分14分）‎ 设c，d，x为实数，c≠0，x为未知数讨论方程在什么情况下有解有解时求出它的解 解：原方程有解的充要条件是：‎ 由条件（4）知，所以再由c≠0，可得 ‎ 又由及x＞0，知，即条件（2）包含在条件（1）及（4）中 再由条件（3）及，知因此，原条件可简化为以下的等价条件组：‎ 由条件（1）（6）知这个不等式仅在以下两种情形下成立：‎ ‎①c＞0，1-d＞0，即c＞0，d＜1；②c＜0，1-d＜0，即c＜0，d＞1.‎ 再由条件（1）（5）及（6）可知 编者说明 ‎1984年的第五题，考查对数函数。具体考查对数方程的有解条件。然而设计“创新到了对数底数”，使得一直看惯了“底数只为单一字母”的考生不知所云。‎ 从而，当c＞0，d＜1且时，或者当c＜0，d＞1且时，原方程有解，它的解是 六．（本题满分16分）‎ ‎1．设，实系数一元二次方程有两个虚数根z1，z2.再设z1，z2在复平面内的对应点是Z1，Z2求以Z1，Z2为焦点且经过原点的椭圆的长轴的长（7分）‎ ‎2．求经过定点M（1，2），以y轴为准线，离心率为的椭圆的左顶点的轨迹方程（9分）‎ 解：1.因为p，q为实数，，z1，z2为虚数，所以 由z1，z2为共轭复数，知Z1，Z2关于x轴对称，‎ 所以椭圆短轴在x轴上又由椭圆经过原点，‎ 可知原点为椭圆短轴的一端点 根据椭圆的性质，复数加、减法几何意义及一元二次方程根与系数的关系，可得椭圆的 短轴长=2b=|z1+z2|=2|p|，‎ 焦距离=‎2c=|z1-z2|=，‎ 长轴长=‎2a=‎ ‎2.因为椭圆经过点M（1，2），且以y轴为准线，所以椭圆在y轴右侧，长轴平行于x轴 设椭圆左顶点为A（x，y），因为椭圆的离心率为，‎ 所以左顶点A到左焦点F的距离为A到y轴的距离的，‎ 从而左焦点F的坐标为 设d为点M到y轴的距离，则d=1‎ 根据及两点间距离公式，可得 ‎ 这就是所求的轨迹方程编者说明 ‎1984年的第六题，考查解析几何。第1小题将椭圆参数藏在复数方程的根中；第2小题求椭圆的轨迹方程，给出的“衍生轨迹”而不是“直接轨迹”。使得广大考生无模式可套。本题得分率也很低。事实上，当年考生，能解答到本卷第六大题的人很少。‎ 七．（本题满分15分）‎ 在△ABC中，∠A，∠B，∠C所对的边分别为，b，c，且c=10，‎ ‎，P为△ABC的内切圆上的动点求点P到顶点A，B，C的距离的平方和的最大值与最小值 解：由，运用正弦定理，有 因为A≠B，所以‎2A=π-2B，即A+B=由此可知△ABC是直角三角形 由c=10，‎ 如图，设△ABC的内切圆圆心为O＇，切点分别为D，E，F，则 AD+DB+EC=但上式中AD+DB=c=10，所以内切圆半径r = EC = 2.‎ 如图建立坐标系，则内切圆方程为：(x-2)2+(y-2)2=4‎ 设圆上动点P的坐标为(x，y)，则 因为P点在内切圆上，所以，‎ 于是S最大值=88-0=88，S最小值=88-16=72‎ 解二：同解一，设内切圆的参数方程为 从而 因为，所以 S最大值=80+8=88，‎ S最小值=80-8=72‎ 编者说明 ‎1984年的第七大题，已经进入后三大题的范畴，是一道典型的综合题。它是三角、解析几何和代数内容的交叉。由于考查的内容常规，本题的设计难度并不大，满分15分，比上一题第六题还少一分。但由于多数考生已被前面的低档、中档题所难倒，因此，大部分考生无缘与第七题见面，因而，从第七题开始，交白卷的甚多。‎ 八．（本题满分12分）‎ 设＞2，给定数列{xn}，其中x1=，求证：‎ ‎1．‎ ‎2．‎ ‎3．‎ ‎1．证：先证明xn＞2(n=1，2，…）用数学归纳法 由条件＞2及x1=知不等式当n=1时成立 假设不等式当n=k(k≥1)时成立 当n=k+1时，因为由条件及归纳假设知 再由归纳假设知不等式成立，所以不等式也成立 从而不等式xn＞2对于所有的正整数n成立 ‎(归纳法的第二步也可这样证：‎ 所以不等式xn>2(n=1，2，…）成立）‎ 再证明由条件及xn>2(n=1，2，…）知 因此不等式也成立 ‎（也可这样证：对所有正整数n有 还可这样证：对所有正整数n有 所以）‎ ‎2．证一：用数学归纳法由条件x1=≤3知不等式当n=1时成立 假设不等式当n=k(k≥1)时成立 当n=k+1时，由条件及知 再由及归纳假设知，上面最后一个不等式一定成立，所以不等式也成立，‎ 从而不等式对所有的正整数n成立 证二：用数学归纳法证不等式当n=k+1时成立用以下证法：‎ 由条件知再由及归纳假设可得 ‎3．证：先证明若这是因为 然后用反证法若当时，有则由第1小题知 因此，由上面证明的结论及x1=可得 即，这与假设矛盾所以本小题的结论成立 编者说明 ‎1984年的第八大题，是本卷正卷的压轴题，是当年正卷上难度最大的题目。考查的内容是数列与不等式的综合。数列不是用通项公式给定，而是用递推式给定。递推式实为教材的延伸，使得绝大多数考生可望而不可及。90%以上的考生与此题无缘，当年在北京本题得满分的仅仅只有两人。‎ 本题的递推数列对以后的若干年影响很大，在全国高中数学界掀起了研究递推数列的热潮。‎ 九．（附加题，本题满分10分，不计入总分）‎ ‎⌒‎ 如图，已知圆心为O、半径为1的圆与直线l相切于点A，一动点P自切点A沿直线l向右移动时，取弧AC的长为，直线PC与直线AO交于点M又知当AP=时，点P的速度为v 求这时点M的速度 解：作CD⊥AM，并设AP = x，AM = y，∠COD=θ 由假设，‎ AC的长为，半径OC=1，可知θ 考虑 ‎∵△APM∽△DCM，‎ 而 编者说明 这是1984年的附加题，在1983年中断一年以后。附加题的重现，是经过了一番讨论的，主要是北大、清华的命题人坚持用附加题选拔尖子学生。当然，这个目的并没有达到，因为考生们连正题都没有完成，所以基本上无人光顾这道附加题，使得此题成为虚设。‎ ‎1984年的数学试题创造了建国以来的难度之最。考后，不少的人（界内和界外）对试题提出了置疑，经过了长达半年的讨论，才基本上在全国统一了看法：难的原因是因为新而活，这个方向是非常正确的，必须坚持，不足之处就是要求急了一点。这种结论对从1985年以后的数学命题取到了良好的导向作用。‎ ‎（有资料表明八四年试题为历年来最难的一次）‎