- 2021-05-13 发布 |
- 37.5 KB |
- 3页


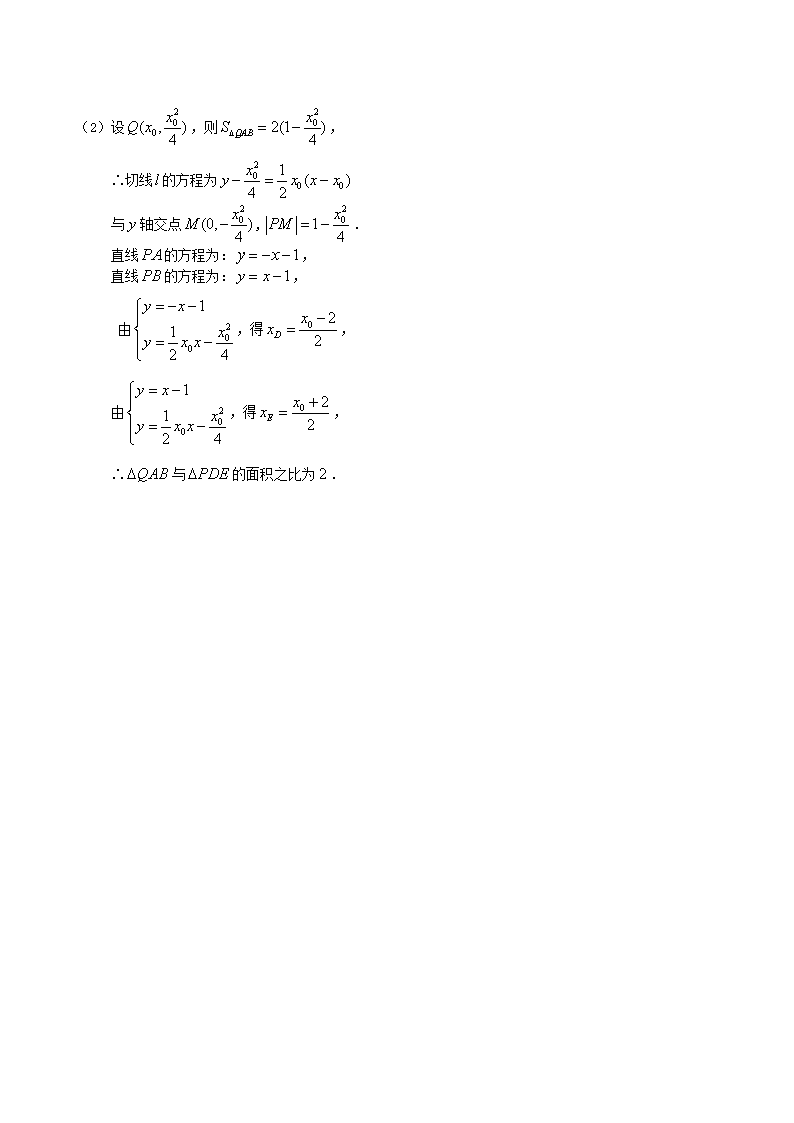
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三维设计广东文人教版2014高考数学第一轮复习考案 轨迹方程的求法 文
第68课 轨迹方程的求法 1.(2019广州二模)高和的两根旗杆笔直地竖在水平地面上, 且相距 , 则地面上观察两旗杆顶端仰角相等的点的轨迹为( ) A. 圆 B. 椭圆 C. 双曲线 D. 抛物线 【答案】A 【解析】设两根旗杆在水平地面上的点分别为 设为轨迹上的点,仰角为, 则,∴, ∴,轨迹是圆. ∴ 所求的轨迹是抛物线. 2.已知点在以原点为圆心的单位圆上运动,则点的轨迹是( ) A.圆 B.抛物线 C.椭圆 D.双曲线 【答案】B 【解析】点在以原点为圆心的单位圆上运动,∴,, 点为 ∴ 所求轨迹方程是抛物线. 3.已知轴上一定点,为椭圆上一动点,求中点的轨迹方程. 【解析】设, ∵是的中点,∴, ∵为椭圆上的点,∴, ∴,即, ∴点的轨迹方程为. 4.已知两圆:,圆:,动圆同时与圆和圆相外切,求动圆的圆心的轨迹方程. 【解析】(1)由已知,点,,,, 如图,设动圆的半径是,则 ∵ 圆与圆外切,∴ ,, ∴ ,即到两定点的距离之差为常数, ∴ 的轨迹是双曲线的左支,,, ∴ ,∴ 动圆圆心的轨迹方程是. 5.(2019珠海二模)已知圆方程:,垂直于轴的直线与圆相切于点(在圆心的右侧),平面上有一动点,若,垂足为,且. (1)求点的轨迹方程; (2)已知为点的轨迹曲线上第一象限弧上一点,为原点,、分别为点的轨迹曲线与轴的正半轴的交点,求四边形的最大面积及点坐标. 【解析】(1)设点坐标为 则, 化简得, ∴点的轨迹方程是. (2)∵、分别为点的轨迹曲线与轴的正半轴的交点, 设点的坐标为, ∴,即, ∴四边形的面积的最大值为, 当四边形的面积的取得最大值时,,即, 此时点坐标为. 6.(2019江西高考)已知三点,曲线上任意一点满足 (1)求曲线的方程; (2)点是曲线上动点,曲线在点处的切线为,点的坐标是,与分别交于点,求与的面积之比. 【解析】(1),, ∴曲线的方程为. (2)设,则, ∴切线的方程为 与轴交点,. 直线的方程为:, 直线的方程为:, 由,得, 由,得, ∴与的面积之比为.查看更多