- 2021-05-13 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考大题空间几何
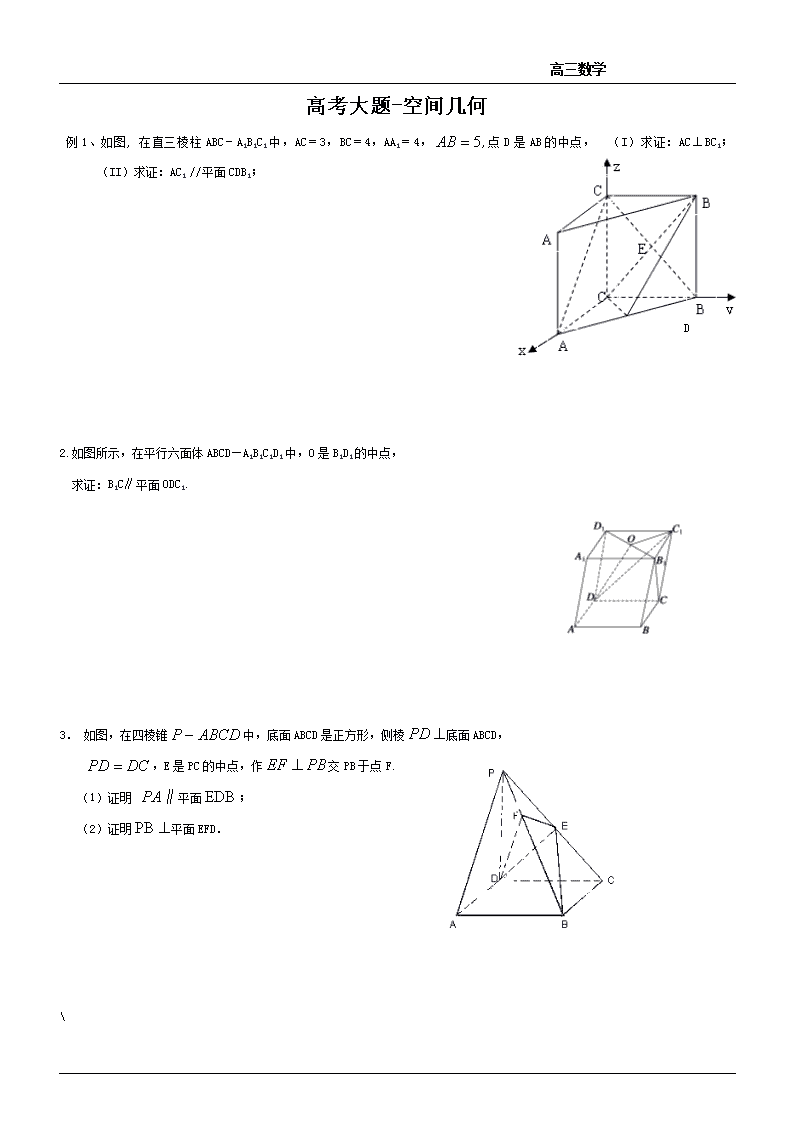
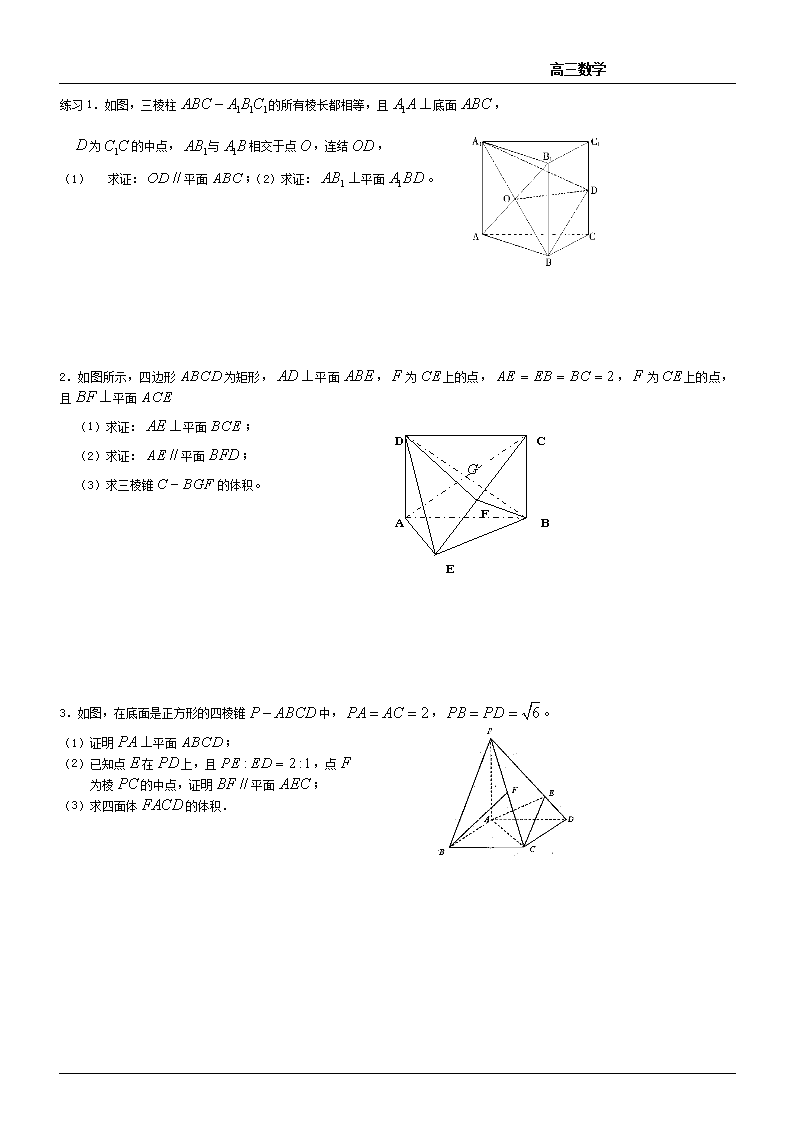
高三数学 高考大题-空间几何 例1、如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,,点D是AB的中点, (I)求证:AC⊥BC1; (II)求证:AC1 //平面CDB1; D 2.如图所示,在平行六面体ABCD—A1B1C1D1中,O是B1D1的中点, 求证:B1C∥平面ODC1. 3. 如图,在四棱锥中,底面ABCD是正方形,侧棱底面ABCD, ,E是PC的中点,作交PB于点F. (1)证明 平面; (2)证明平面EFD. 高三数学 练习1.如图,三棱柱的所有棱长都相等,且底面, 为的中点,与相交于点,连结, (1) 求证:平面;(2)求证:平面。 2.如图所示,四边形为矩形,平面,为上的点,,为上的点,且平面 B A D C F E (1)求证:平面; (2)求证:平面; (3)求三棱锥的体积。 3.如图,在底面是正方形的四棱锥中,,。 (1)证明平面; (2)已知点在上,且,点 为棱的中点,证明平面; (3)求四面体的体积. 高三数学 4. 矩形中,、分别是线段、 第22题图 C D B A P E F 的中点,平面. (1)证明:; (2)在上找一点,使得平面. 5. 如图,在直三棱柱中,,,,. A B C A1 B1 C1 D (1)证明:平面; (2)若是棱的中点,在棱上是否存在一点 ,使平面?证明你的结论. 1.证明:(1)取的中点,连结、,可以证明,故平面. 高三数学 (2)由题意四边形是正方形,则.连结、, 易证得≌,故, 又为的中点,故,∴平面 B A D C F E 2.(1)证明:∵平面,, ∴平面,则 又平面,则 平面 (2)证明:由题意可得是的中点,连接 平面,则, 而,是中点 在中,,平面 (3)解:平面,, 而平面,平面 是中点,是中点, 且, 平面,, 中,, 。 3.(1)证明:因为在正方形中 ∴ 可得在中,。 所以,同理可得, 故平面 (2)取中点,连接,, 连接交于,连接, ∵ 、分别是、的中点, ∴ , ∴ 平面, 高三数学 又是的中点,故, ∴ 平面,故平面平面 ∴ 平面 (3)连接,则,因为平面,则平面 所以,又的面积为,故四面体的体积. 4. (1) 证明:连结,在矩形中,,是线段的中点,故. 第22题图 C D B A P E F 又∵平面,∴ . ∴平面,∴ . (2) 过作交于,则平面, 且. 再过点作交于, 则平面,且. ∴ 平面平面.∴ 平面.故满足的点为所找. 5. (1)证明:∵,∴.∵三棱柱为直三棱柱,∴. ∵,∴平面.∵平面,∴, E F A B C A1 B1 C1 D ∵,则. 在中,,,∴. ∵,∴四边形为正方形. ∴.∵,∴平面 (2)当点为棱的中点时,平面.证明如下: 取的中点,连、、, ∵ 、、分别为、、的中点, ∴.∵平面,平面,∴平面. 同理可证平面. ∵, ∴平面平面. ∵平面, ∴平面.查看更多