中考数学压轴题及答案4

中考数学压轴题及答案4

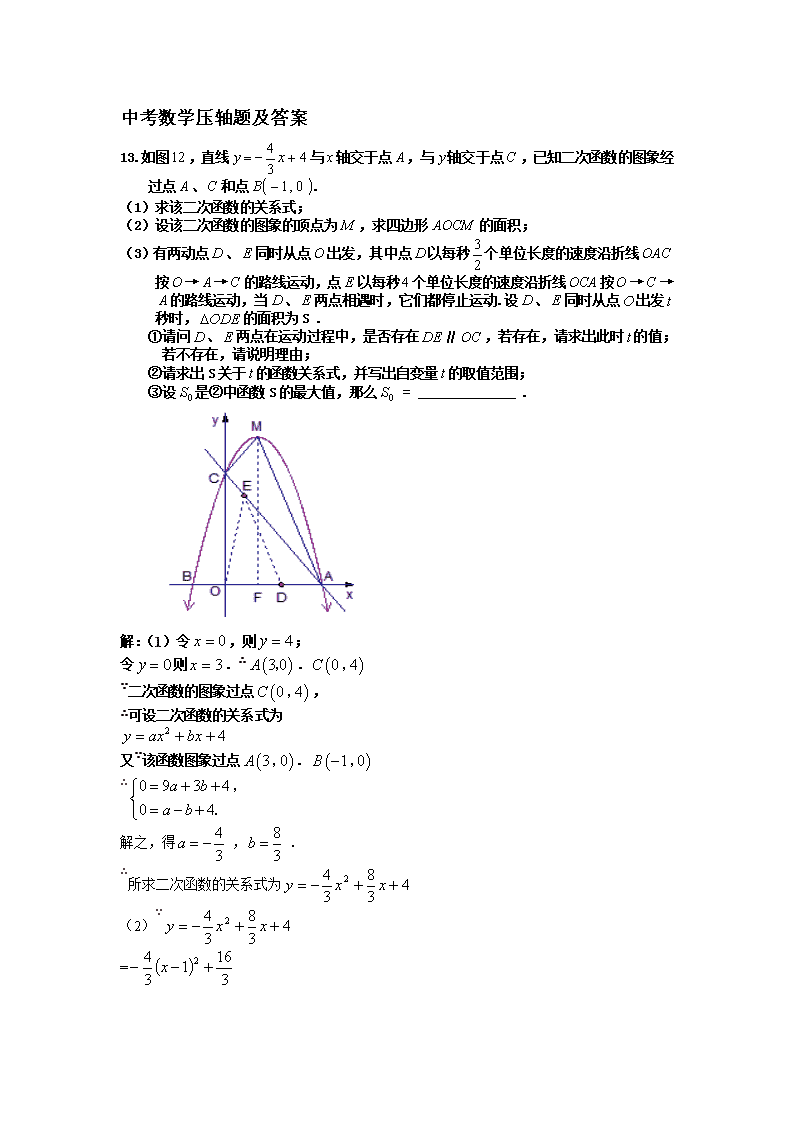
中考数学压轴题及答案 ‎13.如图，直线与轴交于点，与轴交于点，已知二次函数的图象经过点、和点.‎ ‎（1）求该二次函数的关系式；‎ ‎（2）设该二次函数的图象的顶点为，求四边形的面积；‎ ‎（3）有两动点、同时从点出发，其中点以每秒个单位长度的速度沿折线 按→→的路线运动，点以每秒个单位长度的速度沿折线按→→的路线运动，当、两点相遇时，它们都停止运动.设、同时从点出发秒时，的面积为S .‎ ‎①请问、两点在运动过程中，是否存在∥，若存在，请求出此时的值；若不存在，请说明理由；‎ ‎②请求出S关于的函数关系式，并写出自变量的取值范围；‎ ‎③设是②中函数S的最大值，那么 = .‎ 解：（1）令，则；‎ 令则．∴．‎ ‎∵二次函数的图象过点，‎ ‎∴可设二次函数的关系式为 又∵该函数图象过点．‎ ‎∴‎ 解之，得，．‎ ‎∴所求二次函数的关系式为 ‎ ‎（2）∵‎ ‎=‎ ‎∴顶点M的坐标为 ‎ 过点M作MF轴于F ‎∴‎ ‎=‎ ‎∴四边形AOCM的面积为10 ‎ ‎（3）①不存在DE∥OC ‎ ‎∵若DE∥OC，则点D，E应分别在线段OA，CA上，此时，在中，．‎ 设点E的坐标为∴，∴ ∵，‎ ‎∴ ∴ ‎ ‎∵>2，不满足．‎ ‎∴不存在．‎ ‎②根据题意得D，E两点相遇的时间为 ‎（秒）‎ 现分情况讨论如下：‎ ⅰ）当时，；‎ ⅱ）当时，设点E的坐标为 ‎∴，∴‎ ‎∴ ‎ ⅲ）当2 <<时，设点E的坐标为，类似ⅱ可得 设点D的坐标为 ‎∴，‎ ‎∴‎ ‎∴‎ ‎= ‎ ‎③‎ ‎14.已知：如图，抛物线经过、、三点．‎ ‎（1）求抛物线的函数关系式；‎ ‎（2）若过点C的直线与抛物线相交于点E （4，m），请求出△CBE的面积S的值；‎ ‎（3）在抛物线上求一点使得△ABP0为等腰三角形并写出点的坐标；‎ ‎（4）除（3）中所求的点外，在抛物线上是否还存在其它的点P使得△ABP为等腰三角形？若存在，请求出一共有几个满足条件的点（要求简要说明理由，但不证明）；若不存在这样的点，请说明理由．‎ 解：（1）∵抛物线经过点、，‎ ‎∴．‎ 又∵抛物线经过点，‎ ‎∴，．‎ ‎∴抛物线的解析式为．‎ ‎（2）∵E点在抛物线上，‎ ‎∴m = 42–4×6+5 = -3．‎ ‎∵直线y = kx+b过点C（0， 5）、E（4， –3），‎ ‎∴ 解得k = -2，b = 5． ‎ 设直线y=-2x+5与x轴的交点为D，‎ 当y=0时，-2x+5=0，解得x=．‎ ‎∴D点的坐标为（，0）． ‎ ‎∴S=S△BDC + S△BDE ‎=‎ ‎=10．‎ ‎（3）∵抛物线的顶点既在抛物线的对称轴上又在抛物线上，‎ ‎∴点为所求满足条件的点．‎ ‎（4）除点外，在抛物线上还存在其它的点P使得△ABP为等腰三角形．‎ 理由如下：‎ ‎∵，‎ ‎∴分别以、为圆心半径长为4画圆，分别与抛物线交于点、、、、、、、，除去、两个点外，其余6个点为满足条件的点 ‎15.如图，在直角坐标系中，点A的坐标为(－2，0)，连接OA，将线段OA绕原点O顺时针旋转120°，得到线段OB．‎ ‎(1)求点B的坐标；‎ ‎(2)求经过A、O、B三点的抛物线的解析式；‎ ‎(3)在(2)中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由；‎ ‎(4)如果点P是(2)中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．‎ 解：（1）过点B作BD⊥x轴于点D，由已知可得：‎ OB＝OA=2，∠BOD＝60°‎ 在Rt△OBD中，∠ODB＝90°，∠OBD＝30°‎ ‎ ∴OD＝1，DB＝‎ ‎ ∴点B的坐标是（1，）‎ ‎（2）设所求抛物线的解析式为，由已知可得：‎ ‎ 解得：‎ ‎∴所求抛物线解析式为 ‎ ‎（备注：a、b的值各得1分）‎ ‎（3）存在 由 配方后得：‎ ‎∴抛物线的对称轴为 ‎ ‎（也可用顶点坐标公式求出）‎ ‎∵点C在对称轴上，△BOC的周长＝OB+BC+CO；‎ ‎∵OB=2，要使△BOC的周长最小，必须BC+CO最小，‎ ‎∵点O与点A关于直线对称，有CO=CA ‎△BOC的周长＝OB+BC+CO＝OB+BC+CA ‎∴当A、C、B三点共线，即点C为直线AB与抛物线对称轴的交点时，BC+CA最小，此时△BOC的周长最小。‎ 设直线AB的解析式为，则有：‎ 解得：‎ ‎∴直线AB的解析式为 当时，‎ ‎∴所求点C的坐标为（－1，）‎ ‎（4）设P（），则 ①‎ 过点P作PQ⊥y轴于点Q， PG⊥x轴于点G，过点A作AF⊥PQ轴于点F，过点B作BE⊥PQ轴于点E，则PQ=，PG=，由题意可得：‎ ‎ ‎ ‎＝‎ ‎=‎ ‎＝ ②‎ ‎ 将①代入②，化简得： ‎ ‎＝‎ ‎∴当时，△PAB得面积有最大值，最大面积为。‎ 此时 ‎∴点P的坐标为