中考真题训练反比例函数答案

中考真题训练反比例函数答案

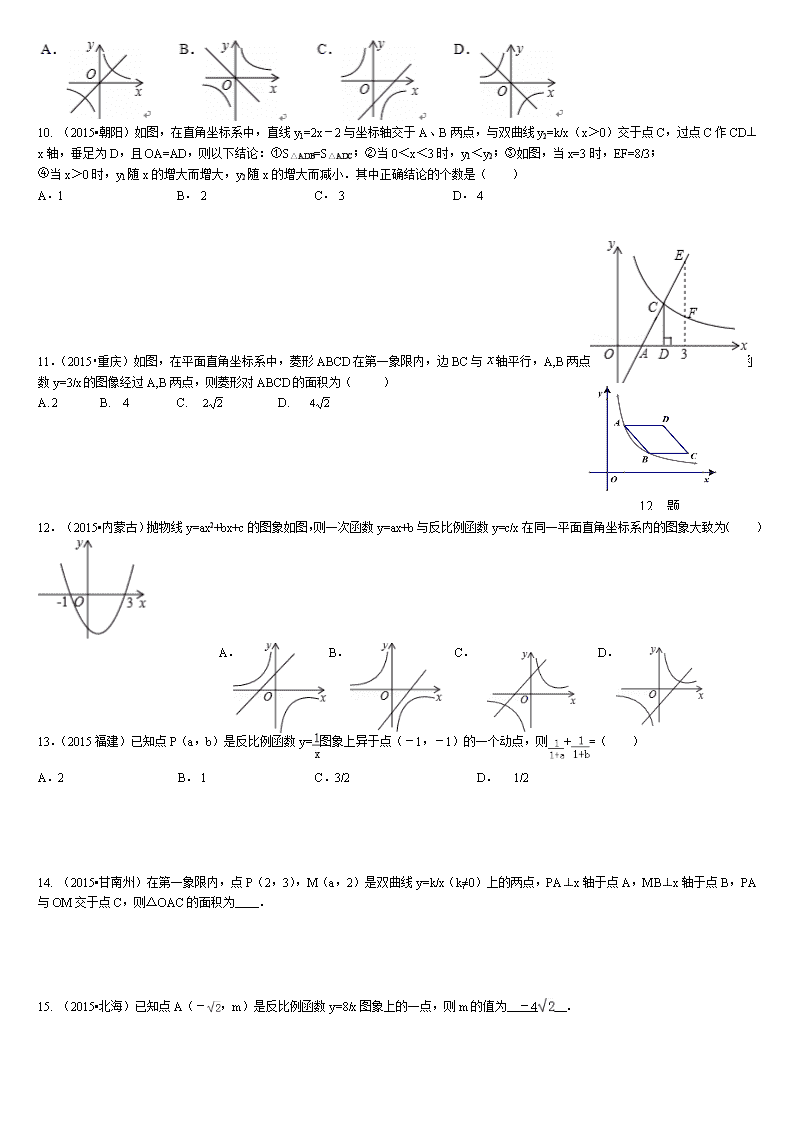
‎1. （2015•福建）如图，已知点A是双曲线y=2/x在第一象限的分支上的一个动点，连接AO并延长交另一分支于点B，过点A作y轴的垂线，过点B作x轴的垂线，两垂线交于点C，随着点A的运动，点C的位置也随之变化．设点C的坐标为（m，n），则m，n满足的关系式为（　　）A．n=﹣2m B． n=﹣2/m C．n=﹣4m D．n=﹣4/m ‎2. （2015，广西钦州）对于函数，下列说法错误的是（　　）‎ A．这个函数的图象位于第一、第三象限B．这个函数的图象既是轴对称图形又是中心对称图形 C．当x＞0时，y随x的增大而增大 D．当x＜0时，y随x的增大而减小 故选：C．‎ ‎3. （2015，广西玉林）如图，反比例函数y=k/x的图象经过二次函数y=ax2+bx图象的顶点（﹣1/2，m）（m＞0），则有（　　）‎ ‎　 A． a=b+2k B． a=b﹣2k C． k＜b＜0 D． a＜k＜0‎ ‎4. （2015，广西）反比例函数y1= m/x(x＞0)的图象与一次函数y2=-x+b的图象交于A、B两点,其中A(1,2),当y2>y1时,x的取值范围(     )‎ A.x＜1 B.1＜x＜2 C.x＞2 D.x＜1或＞2‎ ‎5．（2015•丹东）一次函数y=﹣x+a﹣3（a为常数）与反比例函数y=﹣4/x的图象交于A、B两点，当A、B两点关于原点对称时a的值是（　　） A． 0 B． ﹣3 C． 3 D． 4‎ ‎6. （2015•哈尔滨）点A（﹣1，y1），B（﹣2，y2）在反比例函数y=2/x的图象上，则y1，y2的大小关系是（　　）‎ A． y1＞y2 B． y1=y2 C． y1＜y2 D． 不能确定 ‎7. （2015•青海）已知一次函数y=2x﹣3与反比例函数y=﹣，那么它们在同一坐标系中的图象可能是（　　）‎ ‎　 A． B． C． D． ‎ ‎8. （2015•天津）己知反比例函数y=6/x，当1＜x＜3时，y的取值范围是（　　）‎ A．0＜y＜l B． 1＜y＜2 C． 2＜y＜6 D． y＞6‎ ‎9. （2015•贵州省）若ab＜0，则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是（　　）‎ ‎10. （2015•朝阳）如图，在直角坐标系中，直线y1=2x﹣2与坐标轴交于A、B两点，与双曲线y2=k/x（x＞0）交于点C，过点C作CD⊥x轴，垂足为D，且OA=AD，则以下结论：①S△ADB=S△ADC；②当0＜x＜3时，y1＜y2；③如图，当x=3时，EF=8/3；‎ ‎④当x＞0时，y1随x的增大而增大，y2随x的增大而减小．其中正确结论的个数是（　　）‎ A．1 B． 2 C． 3 D． 4‎ ‎12题图 ‎11．（2015•重庆）如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与轴平行，A,B两点的纵坐标分别为3,1，反比例函数y=3/x的图像经过A,B两点，则菱形对ABCD的面积为（ ）‎ A. 2 B. 4 C. D. ‎ ‎12． （2015•内蒙古）抛物线y=ax2+bx+c的图象如图，则一次函数y=ax+b与反比例函数y=c/x在同一平面直角坐标系内的图象大致为（　　）‎ ‎　 A． B． C． D． ‎ ‎13．（2015福建）已知点P（a，b）是反比例函数y=图象上异于点（﹣1，﹣1）的一个动点，则+=（　　）‎ A．2 B． 1 C．3/2 D． 1/2‎ ‎14. （2015•甘南州）在第一象限内，点P（2，3），M（a，2）是双曲线y=k/x（k≠0）上的两点，PA⊥x轴于点A，MB⊥x轴于点B，PA与OM交于点C，则△OAC的面积为　　．‎ ‎15. （2015•北海）已知点A（﹣，m）是反比例函数y=8/x图象上的一点，则m的值为　﹣4　．‎ ‎16. （2015•齐齐哈尔）如图，点A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点C、D在x轴上，且BC∥AD，四边形ABCD的面积为3，则这个反比例函数的解析式为　 　．‎ ‎17. （2015•宁德）如图，在平面直角坐标系中，反比例函数y=k/x（x＞0）的图象交矩形OABC的边AB于点D，交边BC于点E，且BE=2EC．若四边形ODBE的面积为6，则k=　．‎ ‎19．（2015•铁岭）如图，点A（m，2），B（5，n）在函数y=k/x（k＞0，x＞0）的图象上，将该函数图象向上平移2个单位长度得到一条新的曲线，点A、B的对应点分别为A′、B′．图中阴影部分的面积为8，则k的值为　 ．‎ ‎20．（2015•抚顺）如图，过原点O的直线AB与反比例函数y=k/x（k＞0）的图象交于A、B两点，点B坐标为（﹣2，m），过点A作AC⊥y轴于点C，OA的垂直平分线DE交OC于点D，交AB于点E．若△ACD的周长为5，则k的值为　　．‎ ‎．‎ ‎21． （2015•酒泉）如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y=k/x（k＞x，x＞0）的图象上，点D的坐标为（4，3）．（1）求k的值；（2）若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在函数y=k/x（k＞0，x＞0）的图象上时，求菱形ABCD沿x轴正方向平移的距离．‎ ‎．‎ ‎22. （2015•甘南州）如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴上，函数y=k/x的图象过点P（4，3）和矩形的顶点B（m，n）（0＜m＜4）．（1）求k的值；（2）连接PA，PB，若△ABP的面积为6，求直线BP的解析式．‎ ‎23. （2015•甘南州）如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A，C分别在坐标轴上，点B的坐标为（4，2），直线y=﹣x/2+3交AB，BC于点M，N，反比例函数y=k/x的图象经过点M，N．‎ ‎（1）求反比例函数的解析式；（2）若点P在x轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．‎ ‎24. （2015，广西柳州）如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y=k/x（k＞0）的图象与BC边交于点E．‎ ‎（1）当F为AB的中点时，求该函数的解析式；（2）当k为何值时，△EFA的面积最大，最大面积是多少？‎ ‎25．（2015•湖北十堰）如图，点A（1﹣，1+）在双曲线y=k/x（x＜0）上．（1）求k的值；‎ ‎（2）在y轴上取点B（0，1），为双曲线上是否存在点D，使得以AB，AD为邻边的平行四边形ABCD的顶点C在x轴的负半轴上？若存在，求出点D的坐标；若不存在，请说明理由．‎ ‎．‎ ‎27．（2015•吉林）如图，点A（3，5）关于原点O的对称点为点C，分别过点A，C作y轴的平行线，与反比例函数y=k/x（0＜k＜15）的图象交于点B，D，连接AD，BC，AD与x轴交于点E（﹣2，0）．（1）求k的值；（2）直接写出阴影部分面积之和．‎ ‎28. （2015•黄冈）如图，反比例函数y=k/x的图象经过点A（-1,4),直线y=-x + b(b≠0) 与双曲线y=k/x在第二、四象限分别相交于P，Q 两点，与x 轴、y 轴分别相交于C,D 两点.(1)求k 的值;(2)当b=-2 时，求△OCD 的面积；‎ ‎(3)连接OQ，是否存在实数b,使得S△ODQ=S△OCD？ 若存在，请求出b 的值；若不存在，请说明理由. ‎ ‎30. （2015•贵州）已知反比例函数y=k/x与一次函数y=x+b的图象在第一象限相交于点A（1，﹣k+4）．‎ ‎（1）试确定这两个函数的表达式；（2）求出这两个函数图象的另一个交点B的坐标，并求△A0B的面积．‎ ‎31. （2015•黑龙江）如图，一次函数y=kx+b的图象与反比例函数y=﹣7/x的图象交于A（﹣1，m）、B（n，﹣1）两点 ‎（1）求一次函数的解析式；（2）求△AOB的面积．‎ ‎32．（2015•广东）如图，反比例函数y=k/x（k≠0，x＞0）的图象与直线y=3x相交于点C，过直线上点A（1，3）作AB⊥x轴于点B，交反比例函数图象于点D，且AB=3BD．（1）求k的值；（2）求点C的坐标；‎ ‎（3）在y轴上确定一点M，使点M到C、D两点距离之和d=MC+MD最小，求点M的坐标．‎ ‎33. （2015大连）如图，在平面坐标系中，∠AOB=90°，AB∥x轴，OB=2，双曲线y=k/x经过点B.将△AOB绕点B逆时针旋转，使点O的对应点D落在X轴的正半轴上。若AB的对应线段CB恰好经过点O. ‎ （1） 点B的坐标和双曲线的解析式。(2)判断点C是否在双曲线上，并说明理由。 ‎ ‎ ‎ ‎34. （2015•四川）如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（–3，3/2 ），AB=1，AD=2 ‎ ‎（1）直接写出B、C、D三点的坐标； （2）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数y= k/x(x>0)的图象上，得矩形A＇B＇C＇D＇.求矩形ABCD的平移距离m和反比例函数的解析式。 ‎ ‎ ‎ ‎ ‎ ‎ ‎