中考专题复习坐标找规律

中考专题复习坐标找规律

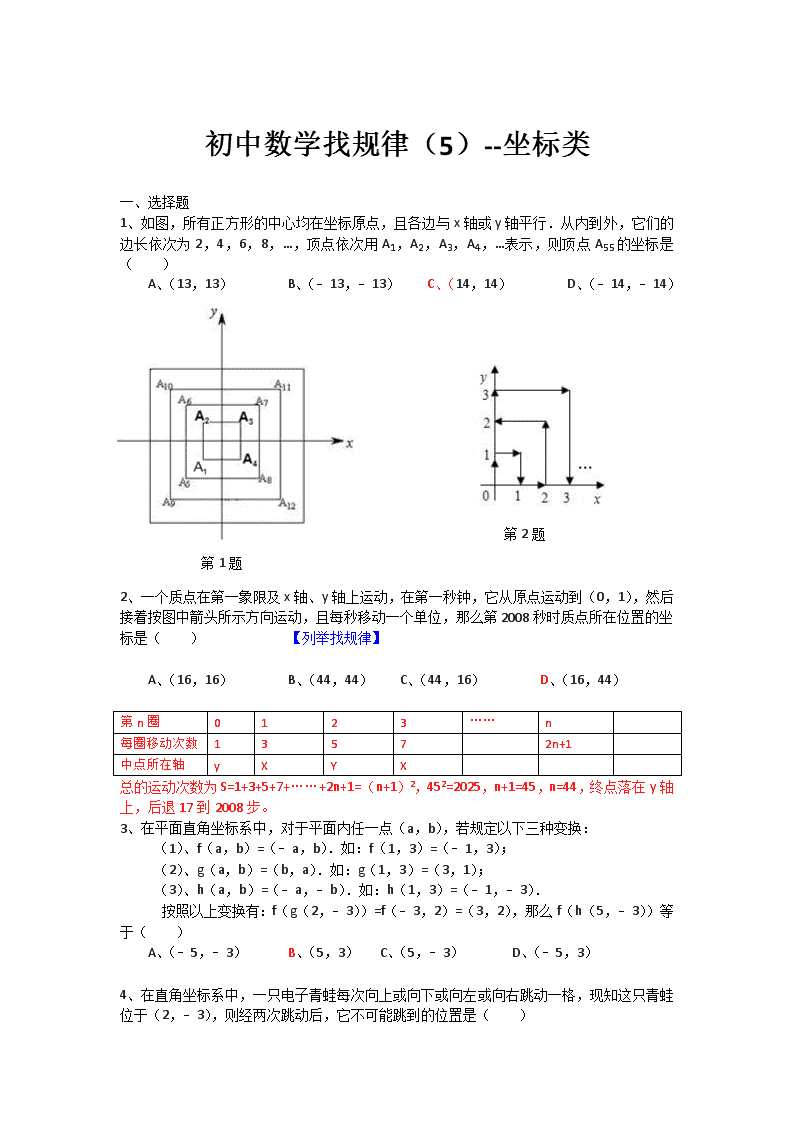
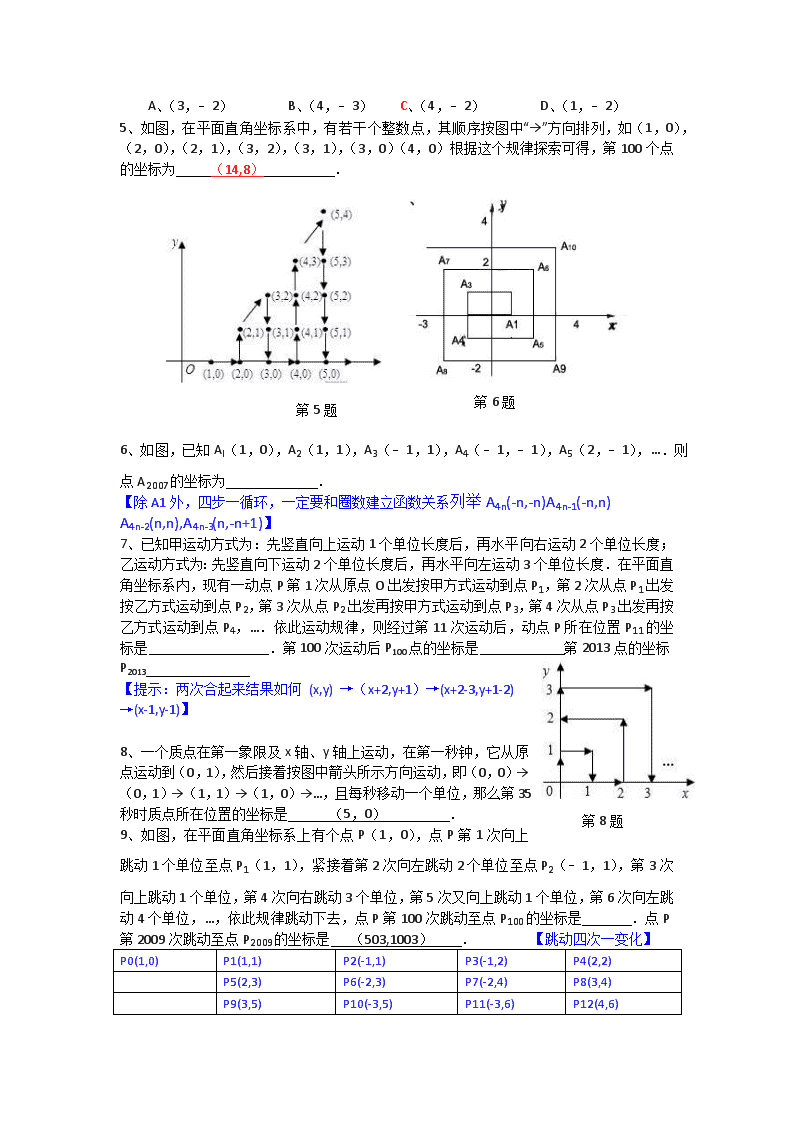
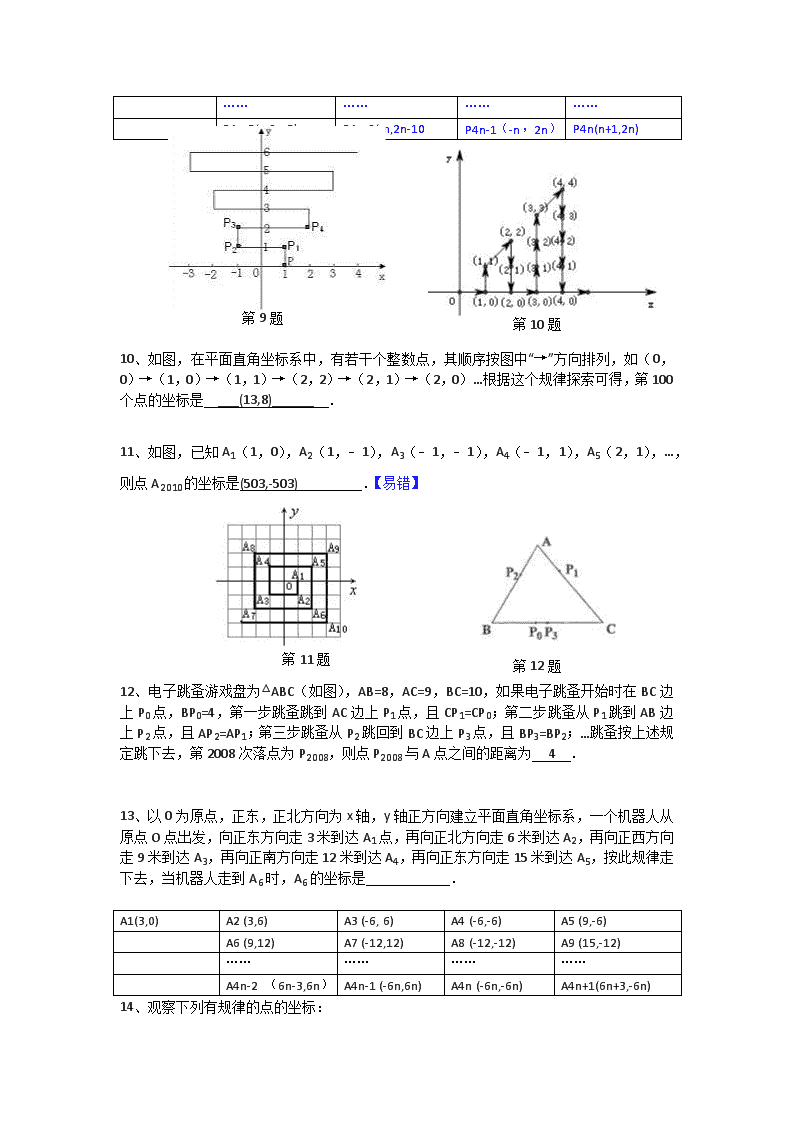
初中数学找规律（5）--坐标类 一、选择题 ‎1、如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1，A2，A3，A4，…表示，则顶点A55的坐标是（　　）‎ 第1题 ‎ A、（13，13） B、（﹣13，﹣13） C、（14，14） D、（﹣14，﹣14）‎ ‎ ‎ ‎ ‎ 第2题 ‎2、一个质点在第一象限及x轴、y轴上运动，在第一秒钟，它从原点运动到（0，1），然后接着按图中箭头所示方向运动，且每秒移动一个单位，那么第2008秒时质点所在位置的坐标是（　　） 【列举找规律】‎ ‎ A、（16，16） B、（44，44） C、（44，16） D、（16，44）‎ 第n圈 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎……‎ n 每圈移动次数 ‎1‎ ‎3‎ ‎5‎ ‎7‎ ‎2n+1‎ 中点所在轴 y X Y X 总的运动次数为S=1+3+5+7+……+2n+1=（n+1）2，452=2025，n+1=45，n=44，终点落在y轴上，后退17到2008步。 ‎ ‎3、在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换：‎ ‎（1）、f（a，b）=（﹣a，b）．如：f（1，3）=（﹣1，3）；‎ ‎（2）、g（a，b）=（b，a）．如：g（1，3）=（3，1）；‎ ‎（3）、h（a，b）=（﹣a，﹣b）．如：h（1，3）=（﹣1，﹣3）．‎ ‎ 按照以上变换有：f（g（2，﹣3））=f（﹣3，2）=（3，2），那么f（h（5，﹣3））等 于（　　）‎ ‎ A、（﹣5，﹣3） B、（5，3） C、（5，﹣3） D、（﹣5，3）‎ ‎4、在直角坐标系中，一只电子青蛙每次向上或向下或向左或向右跳动一格，现知这只青蛙位于（2，﹣3），则经两次跳动后，它不可能跳到的位置是（　　）‎ ‎ A、（3，﹣2） B、（4，﹣3） C、（4，﹣2） D、（1，﹣2）‎ ‎5、如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0）（4，0）根据这个规律探索可得，第100个点的坐标为　 （14,8） 　．‎ 第5题 ‎ 第6题 ‎ ‎ ‎ ‎6、如图，已知Al（1，0），A2（1，1），A3（﹣1，1），A4（﹣1，﹣1），A5（2，﹣1），…．则点A2007的坐标为　 　．‎ ‎【除A1外，四步一循环，一定要和圈数建立函数关系列举A4n(-n,-n)A4n-1(-n,n)‎ A4n-2(n,n),A4n-3(n,-n+1)】‎ 第8题 ‎ ‎7、已知甲运动方式为：先竖直向上运动1个单位长度后，再水平向右运动2个单位长度；乙运动方式为：先竖直向下运动2个单位长度后，再水平向左运动3个单位长度．在平面直角坐标系内，现有一动点P第1次从原点O出发按甲方式运动到点P1，第2次从点P1出发按乙方式运动到点P2，第3次从点P2出发再按甲方式运动到点P3，第4次从点P3出发再按乙方式运动到点P4，…．依此运动规律，则经过第11次运动后，动点P所在位置P11的坐标是　 　 ．第100次运动后P100点的坐标是 第2013点的坐标P2013 ‎ ‎【提示：两次合起来结果如何 (x,y) →（x+2,y+1）→(x+2-3,y+1-2) →(x-1,y-1)】‎ ‎8、一个质点在第一象限及x轴、y轴上运动，在第一秒钟，它从原点运动到（0，1），然后接着按图中箭头所示方向运动，即（0，0）→（0，1）→（1，1）→（1，0）→…，且每秒移动一个单位，那么第35秒时质点所在位置的坐标是　 （5，0）　 ．‎ ‎9、如图，在平面直角坐标系上有个点P（1，0），点P第1次向上跳动1个单位至点P1（1，1），紧接着第2次向左跳动2个单位至点P2（﹣1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P第100次跳动至点P100的坐标是　 　．点P第2009次跳动至点P2009的坐标是　 （503,1003） 　． 【跳动四次一变化】‎ P0(1,0)‎ P1(1,1)‎ P2(-1,1)‎ P3(-1,2)‎ P4(2,2)‎ P5(2,3)‎ P6(-2,3)‎ P7(-2,4)‎ P8(3,4)‎ P9(3,5)‎ P10(-3,5)‎ P11(-3,6)‎ P12(4,6)‎ ‎……‎ ‎……‎ ‎……‎ ‎……‎ P4n-3(n,2n-3)‎ P4n-2(-n,2n-10‎ P4n-1（-n，2n）‎ P4n(n+1,2n)‎ 第9题 ‎ 第10题 ‎ ‎ ‎ ‎ ‎ ‎10、如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（0，0）→（1，0）→（1，1）→（2，2）→（2，1）→（2，0）…根据这个规律探索可得，第100个点的坐标是　___(13,8)______　．‎ ‎11、如图，已知A1（1，0），A2（1，﹣1），A3（﹣1，﹣1），A4（﹣1，1），A5（2，1），…，则点A2010的坐标是(503,-503) 　．【易错】‎ 第11题 ‎ 第12题 ‎ ‎ ‎ ‎ ‎ ‎12、电子跳蚤游戏盘为△ABC（如图），AB=8，AC=9，BC=10，如果电子跳蚤开始时在BC边上P0点，BP0=4，第一步跳蚤跳到AC边上P1点，且CP1=CP0；第二步跳蚤从P1跳到AB边上P2点，且AP2=AP1；第三步跳蚤从P2跳回到BC边上P3点，且BP3=BP2；…跳蚤按上述规定跳下去，第2008次落点为P2008，则点P2008与A点之间的距离为　 4　．‎ ‎13、以0为原点，正东，正北方向为x轴，y轴正方向建立平面直角坐标系，一个机器人从原点O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2，再向正西方向走9米到达A3，再向正南方向走12米到达A4，再向正东方向走15米到达A5，按此规律走下去，当机器人走到A6时，A6的坐标是　 　．‎ A1(3,0)‎ A2 (3,6)‎ A3 (-6, 6)‎ A4 (-6,-6)‎ A5 (9,-6)‎ A6 (9,12)‎ A7 (-12,12)‎ A8 (-12,-12)‎ A9 (15,-12)‎ ‎……‎ ‎……‎ ‎……‎ ‎……‎ A4n-2 （6n-3,6n）‎ A4n-1 (-6n,6n)‎ A4n (-6n,-6n)‎ A4n+1(6n+3,-6n)‎ ‎14、观察下列有规律的点的坐标：‎ 依此规律，A11的坐标为　 ，A12的坐标为　 　．‎ ‎【析：观察图中数据，分下标为奇数和偶数两种情况分析解答．‎ 解答：解：观察点的坐标可以得到以下规律：点的横坐标的值就等于对应的点下标的数值；‎ 纵坐标，当下标是奇数时是正数，后一偶数项的纵坐标依次比前一偶数项的纵坐标多3，故A11的坐标为（11，16），‎ 当下标是偶数时纵坐标是负数，后一偶数项的纵坐标依次为前一偶数项的纵坐标的、、…，故A12的坐标为（12，﹣）．故答案分别为：（11，16）、（12，﹣）．】‎ ‎15、设坐标平面内有一个质点从原点出发，沿x轴跳动，每次向正方向或负方向跳动1个单位，经过5次跳动质点落在点（3，0）（允许重复过此点）处，则质点不同的运动方案共有　 　种．【注意列举】‎ 第17题 ‎16、已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（10，0）、C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为 ．‎ 第16题 ‎ ‎ ‎17．（2013•湛江）如图，所有正三角形的一边平行于x轴，一顶点在y轴上．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1、A2、A3、A4…表示，其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位，则顶点A3的坐标是　_________　，A92的坐标是　_________　．‎ ‎18在平面直角坐标系中，一动点从原点0出发，按向上，向右，向下，向右的方向不断移动，每次移动一个单位长度，得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),……那么点A(4n﹢1）（n为自然数）的坐标为什么？‎ 第18题 ‎19、（2012•泰安）如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（1，1），（1，2），（2，2）…根据这个规律，第2012个点的横坐标为 ‎ 第19题 ‎【解：根据图形，以最外边的正方形边长上的点为准，点的总个数等于x轴上右下角的点的横坐标的平方， 例如：右下角的点的横坐标为1，共有1个，1=12， 右下角的点的横坐标为2时，共有4个，4=22， 右下角的点的横坐标为3时，共有9个，9=32， 右下角的点的横坐标为4时，共有16个，16=42， … 右下角的点的横坐标为n时，共有n2个， ∵452=2025，45是奇数，】‎ 练习1（综合题）如图，在平面直角坐标系中，点A的坐标为（1，1），点B的坐标为（11，1），若点C到直线AB的距离为4，且△ABC是直角三角形，则满足条件的点C有若干个． （1）请在坐标系中把所有这样的点C都找出来，画上实心点，这些点用C1，C2，…表示； （2）写出这些点C1，C2，…对应的坐标． 【问题解决的大致步骤已经知道，只是想问一下，根据A、B两点的坐标特点，直线AB∥x轴，则到直线AB的距离为4的点在平行于直线AB的直线上且距离为4，有两条直线，根据直角三角形斜边上的中线等于斜边的一半，以AB的中点为圆心，半径5画弧与两直线的交点即为直角三角形的第三个顶点，这样的作法的理论依据是什么。‎ 若AB是直角边，则满足条件的有4个点（1，5），（1，-3），（11，5）（11，-3） 若AB是斜边，设C(x，5)，过C作AB边上的高，由射影定理，得， 42=(x-1)(11-x) ‎ 若AB是斜边，设C(x，5)，过C作AB边上的高CE， 由△ACE∽△CBE,得， AE/CE=CE/BE, 即CE2=AE*BE 解得x1=3,x2=9 所以有（3，5），（9，5） ‎ 根据对称性，得另外两点（3，-3）（9，-3） 所以共有8个点符合要求】‎ ‎2、如图，有一系列有规律的点，它们分别是以O为顶点，边长为正整数的正方形的顶点，A1（0，1）、A2（1，1）、A3（1，0）、A4（2，0）、A5（2，2）、A6（0，2）、A7（0，3）、A8（3，3）…，依此规律，点A20的坐标为（　　）‎ · A. （7，0） B. （0，7） C. （7，7） D. （8，8）‎