中考数学专题圆与一次函数代几综合

中考数学专题圆与一次函数代几综合

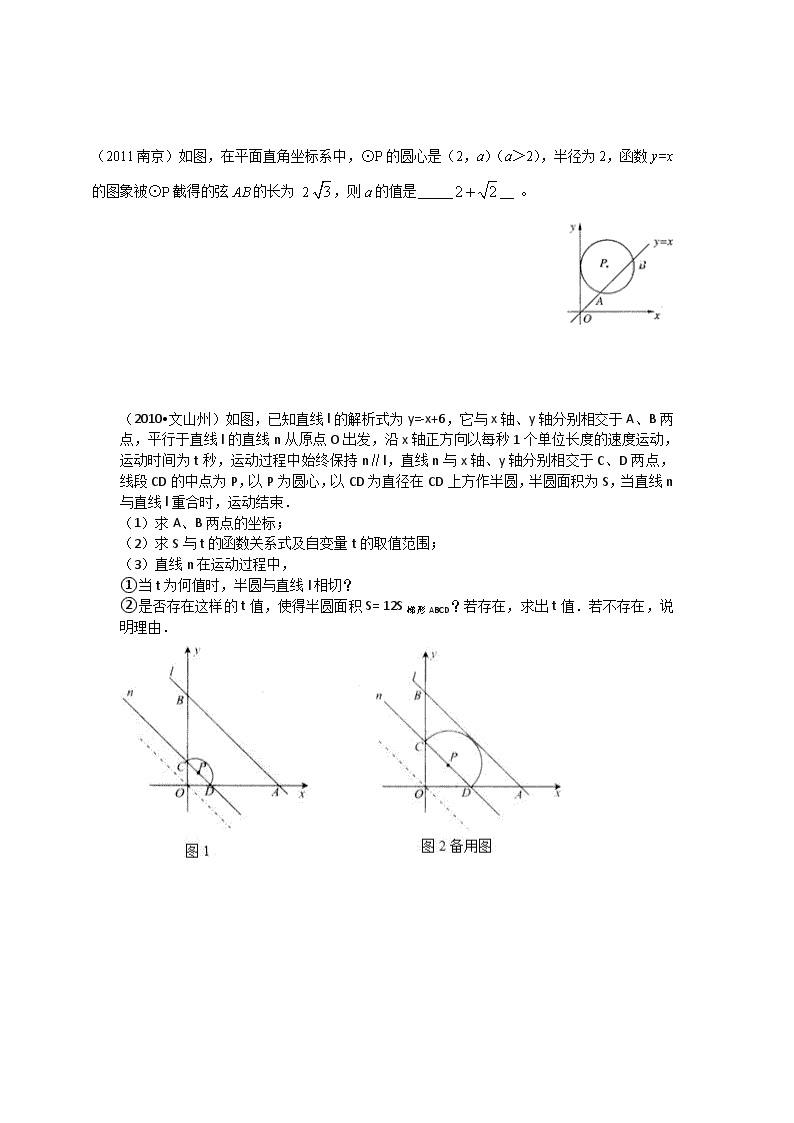
‎（2011南京）如图，在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y=x的图象被⊙P截得的弦AB的长为 2，则a的值是 。‎ ‎（2010•文山州）如图，已知直线l的解析式为y=-x+6，它与x轴、y轴分别相交于A、B两点，平行于直线l的直线n从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，运动时间为t秒，运动过程中始终保持n∥l，直线n与x轴、y轴分别相交于C、D两点，线段CD的中点为P，以P为圆心，以CD为直径在CD上方作半圆，半圆面积为S，当直线n与直线l重合时，运动结束． （1）求A、B两点的坐标； （2）求S与t的函数关系式及自变量t的取值范围； （3）直线n在运动过程中， ①当t为何值时，半圆与直线l相切？ ②是否存在这样的t值，使得半圆面积S= 12S梯形ABCD？若存在，求出t值．若不存在，说明理由． ‎ ‎(2011四川达州，21，6分)如图，在△ABC中，∠A=90°，∠B=60°，AB=3，点D从点A以每秒1个单位长度的速度向点B运动(点D不与B重合)，过点D作DE∥BC交AC于点E．以DE为直径作⊙O，并在⊙O内作内接矩形ADFE，设点D的运动时间为秒．‎ ‎(1)用含的代数式表示△DEF的面积S；‎ ‎(2)当为何值时，⊙O与直线BC相切?‎ ‎【答案】解：（1）∵DE∥BC，∴∠ADE=∠B=60°‎ 在△ADE中，∵∠A=90°‎ ‎∴‎ ‎∵AD=，∴AE= ‎ 又∵四边形ADFE是矩形，‎ ‎∴S△DEF=S△ADE=（‎ ‎∴S=（ ‎ ‎（2）过点O作OG⊥BC于G，过点D作DH⊥BC于H，‎ ‎∵DE∥BC，∴OG=DH，∠DHB=90°‎ 在△DBH中，‎ ‎∵∠B=60°，BD=，AD=，AB=3，‎ ‎∴DH=，∴OG= ‎ 当OG=时，⊙O与BC相切，‎ 在△ADE中，∵∠A=90°，∠ADE=60°，∴，‎ ‎∵AD=，∴DE=2AD=，‎ ‎∴，‎ ‎∴‎ ‎∴当时，⊙O与直线BC相切 ‎（2011湖南娄底，25,10分） 在等腰梯形ABCD中，AD∥BC，且AD=2，以CD为直径作⊙O1，交BC于点E，过点E作EF⊥AB于F，建立如图12所示的平面直角坐标系，已知A，B两点的坐标分别为A(0，2)，B(-2，0).‎ ‎ （1）求C，D两点的坐标.‎ ‎ （2）求证：EF为⊙O1的切线.‎ ‎ （3）探究：如图13，线段CD上是否存在点P，使得线段PC的长度与P点到y轴的距离相等？如果存在，请找出P点的坐标；如果不存在，请说明理由.‎ ‎【答案】（1）连结DE，∵CD是⊙O1的直径，‎ ‎∴DE⊥BC，‎ ‎∴四边形ADEO为矩形.‎ ‎∴OE=AD=2，DE=AO=2.‎ 在等腰梯形ABCD中，DC=AB.‎ ‎∴CE=BO=2，CO=4.‎ ‎∴C(4，0)，D(2，2).‎ ‎（2）连结O1E，在⊙O1中，O1E=O‎1C，‎ ‎∠O1EC=∠O1CE，‎ 在等腰梯形ABCD中，∠ABC=∠DCB.‎ ‎∴O1E∥AB,‎ 又∵EF⊥AB，‎ ‎∴O1E⊥EF.‎ ‎∵E在AB上，‎ ‎∴EF为⊙O1的切线 ‎（3）解法一：存在满足条件的点P.‎ 如右图，过P作PM⊥y轴于M，作PN⊥x轴于N，依题意得PC=PM,‎ 在矩形OMPN中，ON=PM，‎ 设ON=x，则PM=PC=x，CN=4-x，‎ M N P tan∠ABO=.‎ ‎∴∠ABO=60°，‎ ‎∴∠PCN =∠ABO =60°.‎ 在Rt△PCN中，‎ cos∠PCN =，‎ 即,‎ ‎∴x=.‎ ‎∴PN=CN·tan∠PCN=(4-)·=.‎ ‎∴满足条件的P点的坐标为(，).‎ 解法二：存在满足条件的点P，‎ 如右图，在Rt△AOB中，AB=.‎ 过P作PM⊥y轴于M，作PN⊥x轴于N，依题意得PC=PM,‎ 在矩形OMPN中，ON=PM，‎ 设ON=x，则PM=PC=x，CN=4-x，‎ ‎∵∠PCN=∠ABO，∠PCN=∠AOB=90°.‎ ‎∴△PNC∽△AOB，‎ ‎∴，即.‎ 解得x=.‎ 又由△PNC∽△AOB，得 ‎，‎ ‎∴PN= .‎ ‎∴满足条件的P点的坐标为(，).‎ ‎（2010•泰州）如图，⊙O是O为圆心，半径为 5的圆，直线y=kx+b交坐标轴于A、B两点．‎ ‎（1）若OA=OB ‎①求k；‎ ‎②若b=4，点P为直线AB上一点，过P点作⊙O的两条切线，切点分别为C、D，若∠CPD=90°，求点P的坐标；‎ ‎（2）若 k=-12，且直线y=kx+b分⊙O的圆周为1：2两部分，求b．‎ ‎（2010•连云港）如图，在平面直角坐标系中，O为坐标原点，⊙C的圆心坐标为（-2，-2），半径为 2．函数y=-x+2的图象与x轴交于点A，与y轴交于点B，点P为AB上一动点．‎ ‎（1）连接CO，求证：CO⊥AB；‎ ‎（2）若△POA是等腰三角形，求点P的坐标；‎ ‎（3）当直线PO与⊙C相切时，求∠POA的度数；当直线PO与⊙C相交时，设交点为E、F，点M为线段EF的中点，令PO=t，MO=s，求s与t之间的函数关系，并写出t的取值范围．‎ ‎（2009•永州）如图，在平面直角坐标系内，O为原点，点A的坐标为（-3，0），经过A、O两点作半径为 5/2的⊙C，交y轴的负半轴于点B．‎ ‎（1）求B点的坐标；‎ ‎（2）过B点作⊙C的切线交x轴于点D，求直线BD的解析式．‎ ‎•鄂尔多斯）如图，在平面直角坐标系中，直线y= 3/4 x-3与x轴、y轴分别交于A，B两点．现有半径为1的动圆位于原点处，以每秒1个单位的速度向右作平移运动，则经过 7/3或 17/373或 173‎ 秒，动圆与直线AB相切 如图，在平面直角坐标系中，点O1的坐标为（-4，0），以点O1为圆心，8为半径的圆与x轴交于A，B两点，过A作直线l与x轴负方向相交成60°的角，且交y轴于C点，以点O2（13，5）为圆心的圆与x轴相切于点D． （1）求直线l的解析式； （2）将⊙O2以每秒1个单位的速度沿x轴向左平移，当⊙O2第一次与⊙O1外切时，求⊙O2平移的时间．‎ 1. ‎（东营）在△ABC中，∠A＝90°，AB＝4，AC＝3，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．令AM＝x．（1）用含x的代数式表示△ＭNP的面积S；（2）当x为何值时，⊙O与直线BC相切？（3）在动点M的运动过程中，记△ＭNP与梯形BCNM重合的面积为y，试求y关于x的函数表达式，并求x为何值时，y的值最大，最大值是多少？‎ 解：（1）∵MN∥BC，∴∠AMN=∠B，∠ANM＝∠C． ‎ A B C M N P 图 1‎ O ‎ ∴ △AMN ∽ △ABC．‎ ‎∴ ，即．‎ ‎∴ AN＝x． ‎ ‎∴ =．（0＜＜4） ‎ A B C M N D 图 2‎ O Q ‎（2）如图2，设直线BC与⊙O相切于点D，连结AO，OD，则AO =OD =MN．‎ 在Rt△ABC中，BC ＝=5．‎ ‎ 由（1）知 △AMN ∽ △ABC． ‎ ‎∴ ，即． ‎ ‎∴ ，∴ ． ‎ 过M点作MQ⊥BC 于Q，则． 在Rt△BMQ与Rt△BCA中，∠B是公共角，‎ ‎∴ △BMQ∽△BCA．∴ ．∴ ，． ‎ ‎∴ x＝． ∴ 当x＝时，⊙O与直线BC相切． ‎ A B C M N P 图 3‎ O ‎（3）随点M的运动，当P点落在直线BC上时，连结AP，则O点为AP的中点．‎ ‎∵ MN∥BC，∴ ∠AMN=∠B，∠AOM＝∠APC．‎ ‎∴ △AMO ∽ △ABP． ‎ ‎∴ ． AM＝MB＝2． ‎ 故以下分两种情况讨论： ‎ ‎① 当0＜≤2时，． ‎ ‎∴ 当＝2时， ‎ ‎② 当2＜＜4时，设PM，PN分别交BC于E，F．‎ A B C M N P 图 4‎ O E F ‎∵ 四边形AMPN是矩形， ‎ ‎∴ PN∥AM，PN＝AM＝x． ‎ 又∵ MN∥BC， ‎ ‎∴ 四边形MBFN是平行四边形． ‎ ‎∴ FN＝BM＝4－x． ‎ ‎∴ ． ‎ 又△PEF ∽ △ACB． ‎ ‎∴ ．∴＝．‎ 当2＜＜4时，． ‎ ‎ ∴ 当时，满足2＜＜4，． 综上所述，当时，值最大，最大值是2．‎ ‎（无锡）如图，已知点A从（1，0）出发，以1个单位长度/秒的速度沿x轴向正方向运动，以O，A为顶点作菱形OABC，使点B，C在第一象限内，且∠AOC=600，；以P（0，3）为圆心，PC为半径作圆．设点A运动了t秒，求：（1）点C的坐标（用含t的代数式表示）；（2）当点A在运动过程中，所有使⊙P与菱形OABC的边所在直线相切的t的值．‎ ‎ 解：（1）过作轴于，‎ ‎，，‎ ‎，，‎ 点的坐标为． （2分）‎ B A D O P C x y 图1‎ ‎（2）①当与相切时（如图1），切点为，此时，‎ y x B C P O A E 图2‎ ‎，，‎ ‎②当与，即与轴相切时（如图2），则切点为，，‎ 过作于，则， ，．‎ ‎③当与所在直线相切时（如图3），设切点为，交于，‎ 则，，．‎ y x A F C B P O G H 图3‎ 过作轴于，则，‎ ‎，‎ 化简，得，‎ 解得，‎ ‎，．所求的值是，和．‎ ‎2010 山东淄博）如图，在直角坐标系中，以坐标原点为圆心、半径为1的⊙O与x轴交于A，B两点，与y轴交于C，D两点．E为⊙O上在第一象限的某一点，直线BF交⊙O于点F，且∠ABF＝∠AEC，则直线BF对应的函数表达式为　　　　　　　　　　　． ‎ E B O A y x ‎(第17题)‎ C D ‎【答案】，‎ ‎23、如图，在直角坐标系中，点A，B，C的坐标分别为（-1，0），（3，0），（0，3），D（1，a）在直线BC上，⊙A是以A为圆心，AD为半径的圆． （1）求a的值； （2）求证：⊙A与BC相切； （3）在x负半轴上是否存在点M，使MC与⊙A相切，若存在，求点M的坐标；若不存在，说明理由； （4）线段AD与y轴交于点E，过点E的任意一直线交⊙A于P、Q两点，问是否存在一个常数K，始终满足PE•QE=K，如果存在，请求出K的值；若不存在，请说明理由 ‎．‎ ‎（2010安徽蚌埠）已知⊙过点（3，4）,点与点关于轴对称，过作⊙的切线交轴于点。⑴ 求的值；‎ O C P F y G D E x B ‎⑵ 如图，设⊙与轴正半轴交点为，点、是线段上的动点（与点不重合），连接并延长、交⊙于点、，直线交轴于点，若是以为底的等腰三角形，试探索的大小怎样变化，请说明理由。‎ y H A D O x ‎【答案】‎ ‎⑴ ‎ ‎ ‎ ‎（2）试探索的大小怎样变化，请说明理由.‎ 解：当、两点在上运动时（与点不重合），的值不变 过点作于，并延长交于，连接，‎ 交于。‎ 因为为等腰三角形， ，‎ 所以平分 所以弧BN=弧CN，所以， ‎ 所以 ‎ 所以=‎ M N T B O C P F y G D E X 即当、两点在上运动时（与点不重合），的值不变。‎ ‎（2010云南红河哈尼族彝族自治州）如图9，在直角坐标系xoy中，O是坐标原点，点A在x正半轴上，OA=cm，点B在y轴的正半轴上，OB=12cm，动点P从点O开始沿OA以cm/s的速度向点A移动，动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动，移动时间为t（0＜t＜6）s.‎ ‎（1）求∠OAB的度数.‎ ‎（2）以OB为直径的⊙O‘与AB交于点M，当t为何值时，PM与⊙O‘相切？‎ ‎（3）写出△PQR的面积S随动点移动时间t的函数关系式，并求s的最小值及相应的t值.‎ ‎（4）是否存在△APQ为等腰三角形，若存在，求出相应的t值，若不存在请说明理由.‎ ‎ ‎ ‎【答案】解：（1）在Rt△AOB中：tan∠OAB=∴∠OAB=30°‎ ‎（2）如图10，连接O‘P，O‘M. 当PM与⊙O‘相切时，有∠PM O‘=∠PO O‘=90°， △PM O‘≌△PO O‘。 （1）知∠OBA=60°，∵O‘M= O‘B，∴△O‘BM是等边三角形，∴∠B O‘M=60°，可得∠O O‘P=∠M O‘P=60°，∴OP= O O‘·tan∠O O‘P=6×tan60°=，又∵OP=t，∴t=，t=3，即：t=3时，PM与⊙O‘相切.。‎ ‎（3）如图9，过点Q作QE⊥x于点E ∵∠BAO=30°，AQ=4t ∴QE=AQ=2t AE=AQ·cos∠OAB=4t×∴OE=OA-AE=-t ∴Q点的坐标为（-t，2t）‎ S△PQR= S△OAB -S△OPR -S△APQ -S△BRQ =‎ ‎ = = （）‎ ‎ 当t=3时，S△PQR最小=‎ ‎ （4）分三种情况：如图11.‎ 当AP=AQ1=4t时，‎ ‎∵OP+AP=‎ ‎∴t+4t=‎ ‎∴t=‎ 或化简为t=-18‎ 当PQ2=AQ2=4t时 ‎ 过Q2点作Q2D⊥x轴于点D，‎ ‎∴PA=2AD=2A Q2·cosA=t 即t+t =‎ ‎∴t=2‎ 当PA=PQ3时，过点P作PH⊥AB于点H ‎ AH=PA·cos30°=（-t）·=18-3t AQ3=2AH=36-6t 得36-6t=4t，‎ ‎∴t=3.6‎ ‎ 综上所述，当t=2，t=3.6，t=-18时，△APQ是等腰三角形.‎ ‎40。（2010云南楚雄）已知：如图，⊙与轴交于C、D两点，圆心的坐标为（1，0），⊙的半径为，过点C作⊙的切线交于点B（－4，0）．‎ ‎（1）求切线BC的解析式；‎ ‎（2）若点P是第一象限内⊙上一点，过点P作⊙A的切线与直线BC相交于点G，且∠CGP＝120°，求点的坐标；‎ ‎（3）向左移动⊙（圆心始终保持在上），与直线BC交于E、F，在移动过程中是否存在点，使得△AEF是直角三角形？若存在，求出点 的坐标，若不存在，请说明理由．‎ ‎【答案】解：（1）连接，∵是⊙A的切线，∴．‎ ‎∴．‎ ‎∵，∴，∴．‎ ‎∴△∽△，∴．‎ 即，∴．∴点坐标是（0，2）．‎ 设直线的解析式为，∵该直线经过点B（－4，0）与点（0，2），‎ ‎∴ 解得 ‎ ‎ ∴该直线解析式为．‎ ‎（2）连接，过点作．‎ 由切线长定理知 ‎．‎ 在中，∵，‎ ‎∴．‎ 在中，由勾股定理得 ‎ ‎．‎ ‎∴ ．‎ 又∵．‎ ‎∴∽，∴，‎ ‎∴．‎ 则是点的纵坐标，‎ ‎∴，解得．‎ ‎∴点的坐标．‎ ‎ (3)如图示，‎ 当在点的右侧时 ‎ ∵、在⊙上，∴．‎ 若△是直角三角形，则，且为等腰直角三角形．‎ 过点作，在中由三角函数可知 ‎．‎ 又∵∽ ，‎ ‎∴ ，‎ ‎∴．‎ ‎∴，‎ ‎∴点 坐标是．‎ 当在点的左侧时：同理可求点 坐标是．‎ ‎（2010广东深圳）如图10，以点M（—1，0）为圆心的圆与轴、轴分别交于点A、B、C、D，直线与⊙M相切于点H，交轴于点E，求轴于点F。‎ ‎（1）请直接写出OE、⊙M的半径r、CH的长；（3分）‎ ‎（2）如图11，弦HQ交轴于点P，且DP：PH=3：2，求cos∠QHC的值；（3分）‎ ‎（3）如图12，点K为线段EC上一动点（不与E、C重合），连接BK交⊙M于点T，弦AT交轴于点N。是否存在一个常数，始终满足MN·MK，如果存在，请求出的值；如果不存在，请说明理由。（3分）‎ ‎【答案】【答案】‎ ‎（1）、如图①，OE=5，，CH=2‎ ‎（2）、如图②，连接QC、QD，则，‎ 易知，故，‎ F 图①‎ ‎，，由于，‎ ‎；‎ ‎（3）、如图③，连接AK，AM，延长AM，‎ 与圆交于点G，连接TG，则 ‎，‎ 图②‎ F 由于，故，；‎ 而，故 在和中，；‎ 故；‎ ‎;‎ 即：‎ 故存在常数，始终满足 F 图③‎ ‎1‎ 常数 ‎（2010广东茂名）已知⊙O1的半径为R，周长为C．‎ ‎（1）在⊙O1内任意作三条弦，其长分别是、、．求证：++< C； （3分）‎ ‎（备用图）‎ ‎（2）如图，在直角坐标系O中，设⊙O1的圆心为O1．①当直线：与⊙O1相切时，求的值；②当反比例函数的图象与⊙O1有两个交点时，求的取值范围． ‎ ‎（第25题备用图）‎ ‎：‎ ‎【答案】（1）证明：，，．++，因此，++< C．‎ ‎（2）解：①如图，根据题意可知⊙O1与轴、轴分别相切，设直线与⊙O1相切于点M，则O1M⊥l，过点O1作直线NH⊥轴，与交于点N，与轴交于点H，又∵直线与轴、轴分别交于点E（，0）、F（0，），∴OE＝OF＝，∴∠NEO＝45o，∴∠ENO1＝45o，在Rt△O1MN中，O1N＝O1Msin45o＝，∴点N的坐标为N（R，），把点N坐标代入得：，解得：，‎ ‎②如图，设经过点O、O1的直线交⊙O1于点A、D，则由已知，直线OO1：是圆与反比例函数图象的对称轴，当反比例函数的图象与⊙O1直径AD相交时（点A、D除外），则反比例函数的图象与⊙O1有两个交点．过点A作AB⊥轴交轴于点B，过O1作O1C⊥轴于点C，OO1＝O1Csin45o＝，OA＝，所以OB＝AB＝sin45o＝，‎ 因此点A的坐标是A，将点A的坐标 代入，解得：．同理可求得点D的坐标为D，将点D的坐标代入，解得： 。所以当反比例函数的图象与⊙O1有两个交点时，的取值范围是：‎