泰州市2015年中考数学卷

泰州市2015年中考数学卷

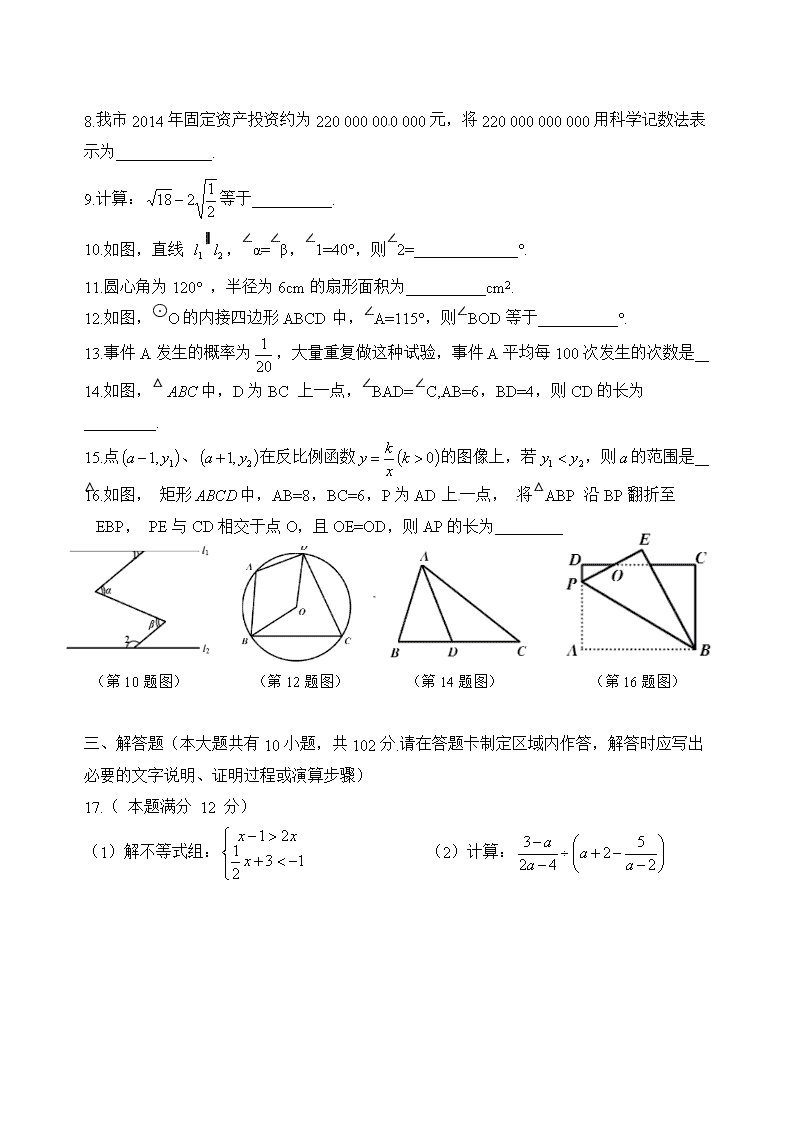
泰州市二〇一五年初中毕业、升学统一考试 数学试卷 第一部分 选择题（共18分）‎ 一、选择题（本大题共有5小题，每小题3分，共18分。在每小题所给出的四个选项中，恰有一项是符合题目要求的）‎ ‎1.的绝对值是 A.-3 B. C. D.3‎ ‎2.下列 4 个数： 其中无理数是 A. B. C.π D.‎ ‎3.描述一组数据离散程度的统计量是 A.平均数 B.众数 C.中位数 D.方差 ‎4.一个几何体的表面展开图如图所示， 则这个几何体是 A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱 ‎ (第4题图) (第5题图) (第6题图)‎ ‎5.如图，在平面直角坐标系xOy中，△由△绕点P旋转得到，则点P的坐标为 A.（ 0， 1） B.（ 1， -1） C.（ 0， -1） D.（ 1， 0）‎ ‎6.如图，△中，AB=AC，D是BC的中点，AC的垂直平分线分别交 AC、AD、AB于点E、O、F，则图中全等的三角形的对数是 A.1对 B.2对 C.3对 D.4对 第二部分 非选择题（共132分）‎ 二、 填空题（本大题共有10小题，每小题3分，共30分）‎ ‎7.=___________.‎ ‎8.我市2014年固定资产投资约为220 000 000 000元，将220 000 000 000用科学记数法表示为____________.‎ ‎9.计算：等于__________.‎ ‎10.如图，直线 ∥，∠α=∠β，∠1=40°，则∠2=_____________°.‎ ‎11.圆心角为120° ，半径为6cm的扇形面积为__________cm2.‎ ‎12.如图，⊙O的内接四边形ABCD中，∠A=115°，则∠BOD等于__________°.‎ ‎13.事件A发生的概率为，大量重复做这种试验，事件A平均每100次发生的次数是 ‎ ‎14.如图，△中，D为BC 上一点，∠BAD=∠C,AB=6，BD=4，则CD的长为_________.‎ ‎15.点、在反比例函数的图像上，若，则的范围是 ‎ 16. 如图， 矩形中，AB=8，BC=6，P为AD上一点， 将△ABP 沿BP翻折至△EBP， PE与CD相交于点O，且OE=OD，则AP的长为__________.‎ ‎ （第10题图） （第12题图） （第14题图） （第16题图）‎ 三、解答题（本大题共有10小题，共102分.请在答题卡制定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎17.（ 本题满分 12 分）‎ ‎（1）解不等式组： （2）计算：‎ ‎18.（本题满分8分）‎ 已知：关于的方程。‎ ‎（1）不解方程：判断方程根的情况；‎ ‎（2）若方程有一个根为3，求的值.‎ ‎19.（本题满分8分）‎ 为了解学生参加社团的情况，从2010年起，某市教育部门每年都从全市所有学生中随机 抽取2000名学生进行调查.图①、图②是部分调查数据的统计图（参加社团的学生每人只能报一项，根据统计图提供的信息解决下列问题：‎ ‎（1）求图②中“科技类”所在扇形的圆心角的度数；‎ ‎（2）该市 2012 年抽取的学生中，参加体育类与理财类社团的学生共有多少人？‎ ‎（3）该市 2014 年共有 50000 名学生，请你估计该市2014年参加社团的学生人数.‎ ‎20.（ 本题满分8分）‎ 一只不透明袋子中装有1个红球、2个黄球，这些球除颜色外都相同。小明搅匀后从中意摸出一个球，记录颜色后放回、搅匀，再从中任意摸出1个球。用画树状图或列表法列出摸出球的所有等可能情况，并求两次摸出的球都是红球的概率。‎ ‎21.（本题满分10分）‎ 某校七年级社会实践小组去商场调查商品销售情况，了解到该商场以每件80元的价格购 进了某品牌衬衫500件， 并以每件120元的价格销售了400件.商场准备采取促销措施，将剩下的衬衫降价销售.请你帮商场计算一下，每件衬衫降价多少元时，销售完这批衬衫正好达到盈利45%的预期目标？‎ ‎22.（ 本题满分10分）‎ 已知二次函数的图像经过点，对称轴是经过且平行于轴的直线。（1）求、的值；‎ ‎（2）如图，一次函数的图像经过点，与轴相交于点，与二次函数的图像相交于另一点B，点B在点P的右侧，， 求一次函数的表达式。‎ ‎23.（ 本题满分 10 分）‎ 如图，某仓储中心有一斜坡AB，其坡度为，顶部A处的高AC为4m，B、C在同一水平地面上。‎ ‎（1）求斜坡AB的水平宽度BC；‎ ‎（2）矩形DEFG为长方形货柜的侧面图，其中DE=2.5m，EF=2m.将该货柜沿斜坡向上运送，当BF=3.5m时，求点D离地面的高。‎ ‎（，结果精确到0.1m）‎ ‎24.（ 本题满分 10 分）‎ 如图，△ABC 中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F。‎ ‎（1）试说明DF是⊙O的切线；‎ ‎（2）若 AC=3AE，求。‎ ‎25.（ 本题满分 12 分）‎ 如图，正方形ABCD的边长为8cm，E、F、G、H分别是AB、BC、CD、DA 上的动点，且AE=BF=CG=DH.‎ ‎（1）求证：四边形EFGH是正方形；‎ ‎（2）判断直线EG是否经过一个定点，并说明理由；‎ ‎（3）求四边形EFGH面积的最小值。‎ ‎26.（ 本题满分 14 分）‎ 已知一次函数的图像与 轴、轴分别相交于点A、B，点P在该函数图像上， P到轴、轴的距离分别为、。‎ ‎（1）当P为线段AB的中点时，求的值；‎ ‎（2）直接写出的范围，并求当时点P的坐标；‎ ‎（3）若在线段AB 上存在无数个P点，使（为常数）， 求的值.‎ 参考答案