2014云南昆明中考数学

2014云南昆明中考数学

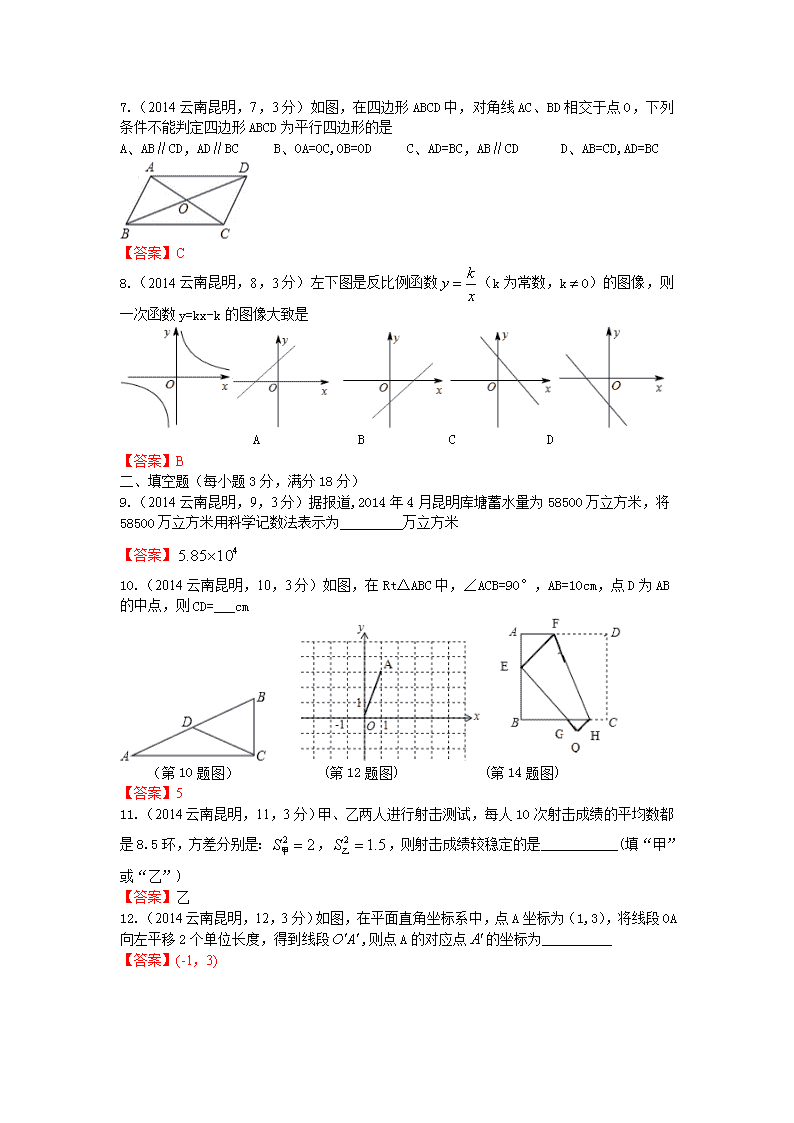
云南昆明市2014年初中学业水平考试 一、 选择题（每小题3分，共24分）‎ ‎1.（2014云南昆明，1，3分）的相反数是 A、 ‎ B、 C、2 D、-2‎ ‎【答案】B 2. ‎（2014云南昆明，2，3分）左下图是由3个完全相同的小正方形体组成的立体图形，它的主视图是 ‎ A． B． C． D．‎ ‎【答案】B 3. ‎（2014云南昆明，3，3分）已知，是一元二次方程的两个实数根，则等于 A、 ‎-4 B、-1 C、1 D、4‎ ‎【答案】C 4. ‎（2014云南昆明，4，3分）下列运算正确的是 A、 B、 C、 D、‎ ‎【答案】D ‎5.（2014云南昆明，5，3分）如图，在△ABC中，∠A=50°，∠ABC=70°，BD平分∠ABC，则∠BDC的度数是 A、85° B、80° C、75° D、70°‎ ‎【答案】A 6. ‎（2014云南昆明，6，3分）某果园2011年水果产量为100吨，2013年水果产量为144吨，求该果园水果产量的年平均增长率，设该果园水果产量的年平均增长率为x，则根据题意可列方程为 A、 ‎ B、 C、 D、‎ ‎【答案D 7. ‎（2014云南昆明，7，3分）如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是 A、 AB∥CD，AD∥BC B、OA=OC,OB=OD C、AD=BC，AB∥CD D、AB=CD,AD=BC ‎【答案】C 8. ‎（2014云南昆明，8，3分）左下图是反比例函数（k为常数，k0）的图像，则一次函数y=kx-k的图像大致是 ‎ ‎ ‎ A B C D ‎【答案】B 二、 填空题（每小题3分，满分18分） ‎ ‎9.（2014云南昆明，9，3分）据报道,2014年4月昆明库塘蓄水量为58500万立方米，将58500万立方米用科学记数法表示为_________万立方米 ‎【答案】‎ ‎10.（2014云南昆明，10，3分）如图，在Rt△ABC中，∠ACB=90°，AB=10cm，点D为AB的中点，则CD=___cm ‎ ‎ ‎（第10题图） (第12题图) (第14题图)‎ ‎【答案】5‎ 11. ‎（2014云南昆明，11，3分）甲、乙两人进行射击测试，每人10次射击成绩的平均数都是8.5环，方差分别是：，，则射击成绩较稳定的是___________(填“甲”或“乙”)‎ ‎【答案】乙 12. ‎（2014云南昆明，12，3分）如图，在平面直角坐标系中，点A坐标为（1,3），将线段OA向左平移2个单位长度，得到线段,则点A的对应点的坐标为__________ ‎ ‎【答案】(-1，3)‎ 11. ‎（2014云南昆明，13，3分）要使分式有意义，则x的取值范围是_______‎ ‎【答案】‎ 12. ‎（2014云南昆明，14，3分）如图，将边长为6cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在点Q处，EQ与BC交于点G，则△EBG的周长是_______cm ‎【答案】12‎ 三、 解答题（共9题，满分58分）‎ ‎15.（2014云南昆明，15，5分）计算：‎ ‎【答案】解：原式==3‎ ‎16（2014云南昆明，16，5分）已知：如图，点A、B、C、D在同一直线上，AB=CD，AE∥CF且AE=CF 求证：∠E=∠F ‎【答案】（1）证明： AE∥CF，则∠A=∠FCD ‎ ‎ 在△ABE与△DFE中 ‎ ‎ ‎ ‎ ∴△ABE≌△CDF ‎ ‎ ∴∠E=∠F ‎17.（2014云南昆明，17，5分）先化简，再求值：，其中 ‎【答案】解：原式===‎ 18. ‎（2014云南昆明，18，6分）某校计划开设4门选修课：音乐、绘画、体育、舞蹈,学校采取随机抽样的方法进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门）对调查结果进行统计后，绘制了如下两幅不完整的统计图 根据以上统计图提供的信息，回答下列问题：‎ （1） 此次调查抽取的学生人数为a=_____人，其中选择“绘画”的学生人数占抽样人数的百分比为b=_______‎ （2） 补全条形统计图 （3） 若该校有2000名学生，请估计全校选择“绘画”的学生大约有多少人？‎ ‎【答案】解：解：（1）100 40%‎ ‎ （2） 作图如上所示 （3）大约有2000*40%=800 ‎ 19. ‎（2014云南昆明，19，6分）九年级某班同学在毕业晚会中进行抽奖活动，在一个不透明的口袋中有三个完全相同的小球，把它们分别标号为1,2,3，随机摸出一个小球记下标号后放回摇匀，再从中随机摸出一个小球记下标号 （1） 请用列表或画树形图的方法（只选择其中一种），表示两次摸出小球上的标号的所有结果 （2） 规定当两次摸出的小球标号相同时中奖，求中奖的概率 ‎【答案】解：解：（1）画树状图得： 则共有9种等可能的结果； （2）“两次取的小球的标号相同”的概率为，即中奖概率为 20. ‎（2014云南昆明，20，6分）如图，在数学实践课中，小明为了测量学校旗杆CD的高度，在地面A处放置高度为1.5米的测角仪AB，测得旗杆顶端D的仰角为32°，AC=22米，求旗杆CD的高度（结果精确到0.1米，参考数据：sin32°=0.53，cos32°=0.85，tan32°=0.62）‎ ‎【答案】解：由题意得AC=BE=22，∠EBD=32°，DE=BEtan32°≈13.64m． CD=EC+ED=13.64+1.5≈15.14m． 答：旗杆高度约15.14m．‎ ‎21（2014云南昆明，21，8分）某校运动会需要购买A、B两种奖品，若购买A种奖品3件和B种奖品2件，共需60元；若购买A种奖品5件和B种奖品3件，共需95元 （1） 求A、B两种奖品的单价各是多少元？‎ （2） 学校计划购买A、B两种奖品共100件，购买费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍，设购买A种奖品m件，购买费用为W元，写出W（元）与m(件)之间的函数关系式，求出自变量m的取值范围，并确定最少费用W的值 ‎【答案】解：（1）设A种奖品每件x元，B种奖品每件y元依题意得：‎ ‎ 解得：‎ ‎ （2）设A种奖品m件，则B种奖品100-m件 ，依题意得 ‎ 解得：70《m《75‎ W=10m+15（100-m）=1500-5m(70《m《75)‎ 当m=75的时候w最小=1125‎ 答：A种奖品每件10元，B种奖品每件15元，当m=75的时候w最小=1125‎ ‎22（2014云南昆明，22，8分）如图，在△ABC中，∠ABC=90°，D是边AC上的一点，连接BD，使∠A=2∠1，E是BC上的一点，以BE为直径的圆O经过点D （1） 求证：AC是圆O的切线 （2） 若∠A=60°，圆O的半径为2，求阴影部分的面积（结果保留根号和π）‎ ‎【答案】证明：（1）如图，连接OD，OB=OD，则∠1=∠BDO ‎ ∠DOC=2∠1=∠A 在Rt△ABC中，∠A+∠C=90°，即∠DOC+∠C=90°‎ ‎ ∴∠ODC=90°即OD⊥DC ‎ ∴AC为圆O的切线 ‎ （2）当∠A=60°时，即在Rt△OCD中，∠C=30°，OD=r=2‎ ‎ ∴∠DOC=60°，CD=2‎ ‎ =2 =‎ 23. ‎（2014云南昆明，23，9分）如图，在平面直角坐标系中，抛物线与x轴交于点A（-2,0）、B（4,0）两点，与y轴交于点C （1） 求抛物线的解析式 （2） 点P从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个也停止运动，当△PBQ存在时，求运动多少秒使△PBQ的面积最大，最大面积是多少？‎ （3） 当△PBQ的面积最大时，在BC下方的抛物线上存在点M，使，求M点坐标 ‎【答案】解：（1）经过A（-2,0）、B（4,0）‎ ‎ 解得：‎ ‎ ∴‎ ‎ （2）设经过t秒时，可知PB=6-3t BQ=t ,B（4,0）C（0，-3），则BC=5过Q点作 ‎ ‎ QK⊥X轴于K点 ‎ 可知：△BKQ∽△BOC ‎ ∴ 即 ∴KQ=‎ ‎ ∴==‎ ‎ 当t=1的时候取最大值为 ‎ （3）当取最大值时，，即 ‎ M在抛物线上，且在BC下方设M（t，） ‎ ‎ 过M点作y轴的平行线交BC于N点,交x轴于R点，因为B（4.0），C（0，-3）则BC直线解析式为：y=x-3‎ 则N点坐标为（t,t-3）‎ ‎ ===‎ ‎∴3=‎ 解得t=2 ∴M（2，-3）‎