广西北海中考数学试卷和答案
2018年广西北部湾经济区六市同城初中毕业升学统一考试
(六市:南宁、北海、钦州、防城港、崇左和来宾市)
数 学
(考试时间:120分钟 满分:120分)
一、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的)
1. -3的倒数是 ( )
A. -3 B. 3 C. D.
2. 下列美丽的壮锦图案是中心对称图形的是 ( )
A B C D
3. 2018年俄罗斯世界杯开幕式于6月14日在莫斯科卢日尼基球场举行,该球场可容纳81000名观众,其中数据81000用科学记数法表示为 ( )
A. 81×103 B. 8.1×103 C. 8.1×104 D. 0.81×105
4. 某球员参加一场篮球比赛,比赛分4节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分
A. 7分 B. 8分 ( )
C. 9分 D. 10分
5. 下列运算正确的是 ( )
A. a(a+1) = a2+1 B. (a2)3 = a5 C. 3a2+a=4a3 D. a5÷a2 = a3
6. 如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于 ( )
A. 40° B. 45°
C. 50° D. 55°
7. 若m>n,则下列不等式正确的是 ( )
A. m-2
-8n
8. 从-2,-1, 2这三个数中任取两个不同的数相乘,积为正数的概率是 ( )
A. B. C. D.
9. 将抛物线向左平移2个单位后,得到新抛物线的解析式为 ( )
A. B. C. D.
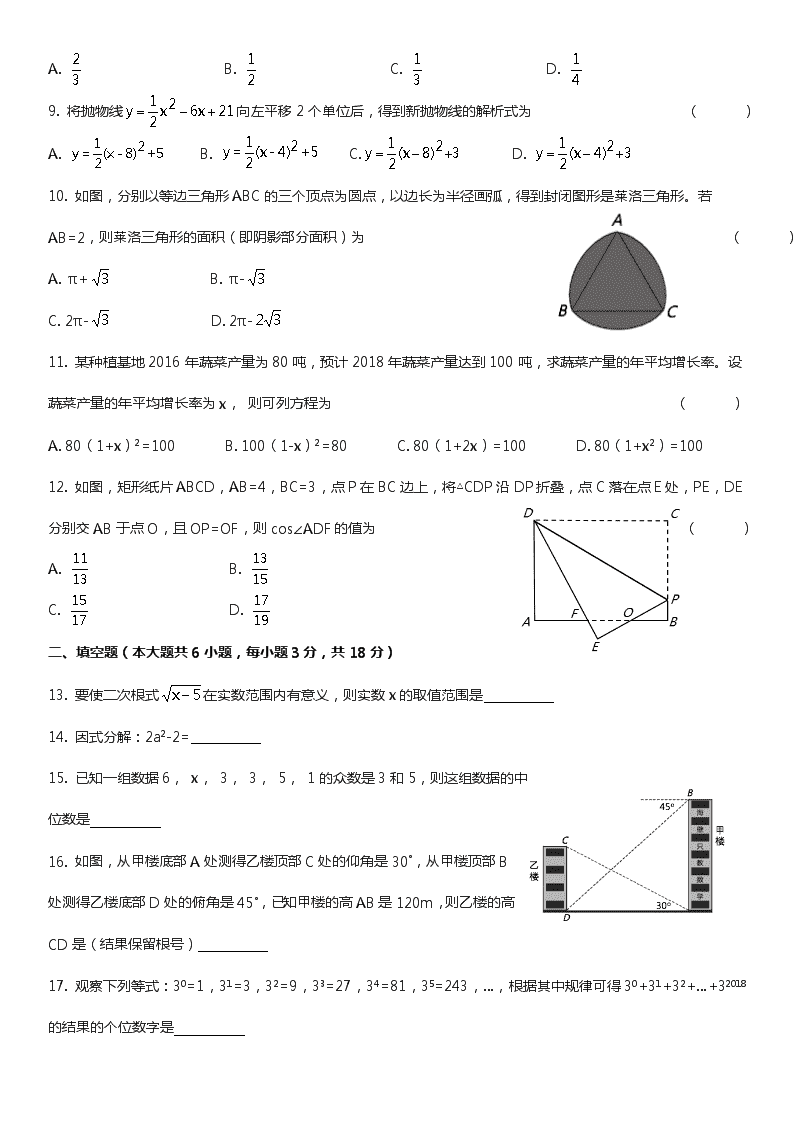
10. 如图,分别以等边三角形ABC的三个顶点为圆点,以边长为半径画弧,得到封闭图形是莱洛三角形。若AB=2,则莱洛三角形的面积(即阴影部分面积)为 ( )
A. π+ B. π-
C. 2π- D. 2π-
11. 某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率。设蔬菜产量的年平均增长率为x, 则可列方程为 ( )
A. 80(1+x)2=100 B. 100(1-x)2=80 C. 80(1+2x)=100 D. 80(1+x2)=100
12. 如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O,且OP=OF,则cos∠ADF的值为 ( )
A. B.
C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
13. 要使二次根式在实数范围内有意义,则实数x的取值范围是
14. 因式分解:2a2-2=
15. 已知一组数据6, x, 3, 3, 5, 1的众数是3和5,则这组数据的中位数是
16. 如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是(结果保留根号)
17. 观察下列等式:30=1,31=3,32=9,33=27,34=81,35=243,…,根据其中规律可得30+31+32+…+32018的结果的个位数字是
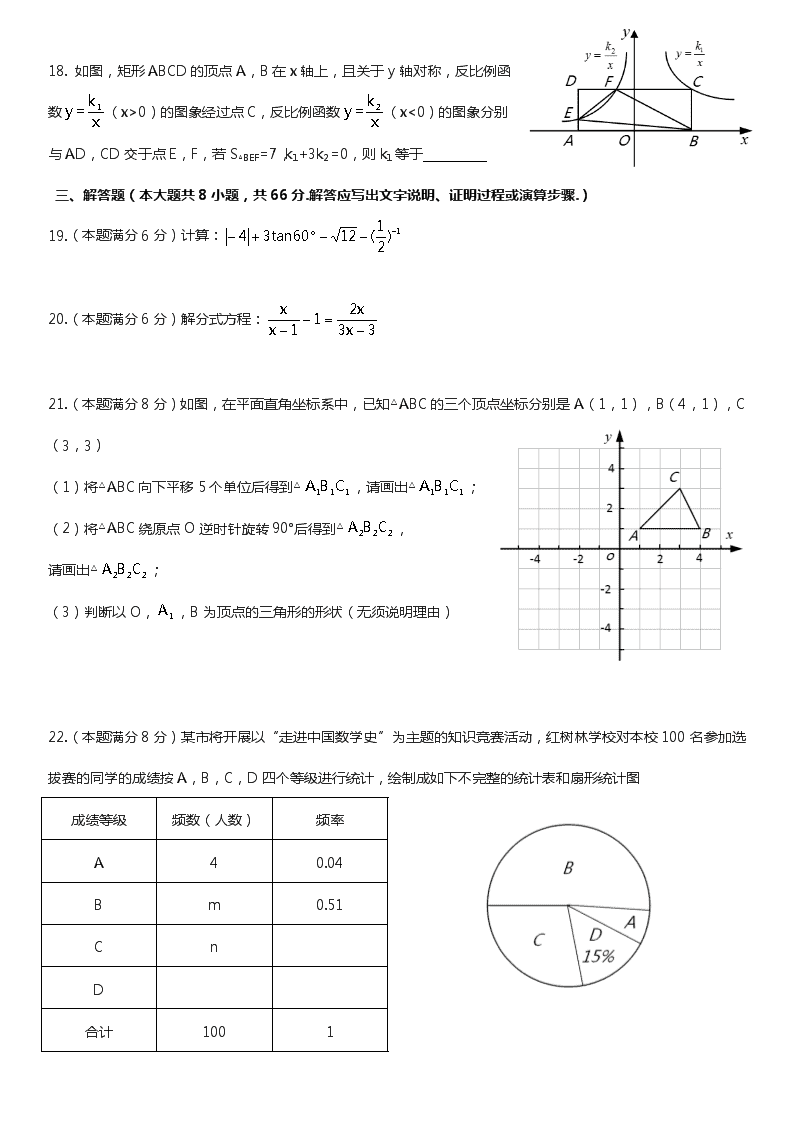
18. 如图,矩形ABCD的顶点A,B在x轴上,且关于y轴对称,反比例函数(x>0)的图象经过点C,反比例函数(x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于
三、解答题(本大题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
19.(本题满分6分)计算:
20.(本题满分6分)解分式方程:
21.(本题满分8分)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3)
(1)将△ABC向下平移5个单位后得到△,请画出△;
(2)将△ABC绕原点O逆时针旋转90°后得到△,
请画出△;
(3)判断以O,,B为顶点的三角形的形状(无须说明理由)
22.(本题满分8分)某市将开展以“走进中国数学史”为主题的知识竞赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图
成绩等级
频数(人数)
频率
A
4
0.04
B
m
0.51
C
n
D
合计
100
1
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应圆心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或列表法求出恰好选中“1男1女”的概率
23.(本题满分8分)如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF
(1)求证:平行四边形ABCD是菱形;
(2)若AB=5,AC=6. 求平行四边形ABCD的面积
24.(本题满分10分)某公司在甲,乙两仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨
(1)求甲,乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲,乙两仓库到工厂的运价分别为120元/吨和100元/吨,经协商,从甲仓库到工厂的运价可优惠a元/吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明,随着m的增大,W的变化情况
25.(本题满分10分)如图,△ABC内接于⊙O,∠CBG =∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD
(1)求证:PG与⊙O相切;
(2)若,求的值;
(3)在(2)的条件下,若⊙O的半径为8,PD= OD,求OE的长
26.(本题满分10分)如图,抛物线y=ax²-5ax+c与坐标轴分别交于A,C,E三点,其中A(-3,0),C(0,4)。点B在x轴上, AC=BC, 过点B做BD⊥x轴交抛物线于点D,点M,N分别是线段CO, BC上的动点,且CM=BN,连接MN,AM,AN
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值