- 2021-05-10 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013中考数学冲刺模拟卷5
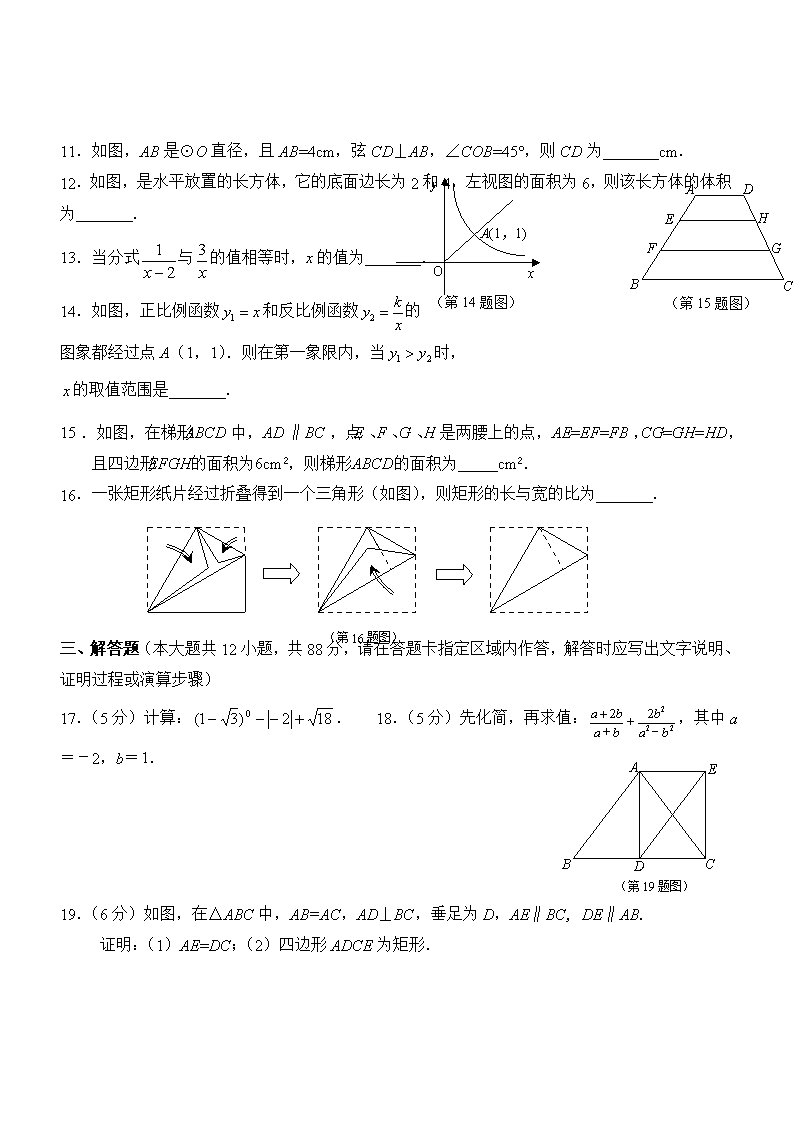
2013中考数学冲刺模拟卷5 选择题(本大题共有6小题,每小题2分,共12分) 1.的相反数是( ).A. B. C.5 D. 2.下列运算正确的是( ).A. B. C. D. 3.为迎接2014年青奥会,在未来两到三年时间内,一条长53公里,总面积约11000亩的鸀色长廊将串起南京的观音门、仙鹤门、沧波门等8座老城门遗址.数据11000用科学记数法可表示为( ). A. B. C. D. 4.如图,不等式组的解集在数轴上表示正确的是( ). -1 0 1 A. -1 0 1 B. -1 0 1 C. -1 0 1 D. 5.如图,在网格的两个格点上任意摆放黑、白两个棋子,且两棋子不在同一条格线上.其中恰好如图示位置摆放的概率是( ).A. B. C. D. O A B l (第6题图) (第5题图) 6.如图,在扇形纸片AOB中,OA =10,ÐAOB=36°,OB在桌面内的直线l上.现将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA落在l上时,停止旋转.则点O所经过的路线长为( ). A. B. C. D. 二、填空题(本大题共10个小题,每小题2分,共20分.不需写出解答过程,请把正确答案直接填写在答题纸相应位置上) 7.数据3,5,5,,1,1,1的众数是 . 8.分解因式的结果是 . 9.如图,已知AB∥CD,°, 则为 °. 10.观察:,…,则 (n为正整数). (第9题图) A B C D F E 4 2 (第12题图) (第11题图) A C D O B 11.如图,AB是⊙O直径,且AB=4cm,弦CD⊥AB,∠COB=45°,则CD为 cm. D B C E F A G H (第15题图) (第14题图) O A(1,1) y x 12.如图,是水平放置的长方体,它的底面边长为2和4,左视图的面积为6,则该长方体的体积为 . 13.当分式与的值相等时,x的值为 . 14.如图,正比例函数和反比例函数的 图象都经过点A(1,1).则在第一象限内,当时, 的取值范围是 . 15.如图,在梯形ABCD中,AD∥BC,点E、F、G、H是两腰上的点,AE=EF=FB,CG=GH=HD,且四边形EFGH的面积为6cm2,则梯形ABCD的面积为 cm2. 16.一张矩形纸片经过折叠得到一个三角形(如图),则矩形的长与宽的比为 . (第16题图) 三、解答题(本大题共12小题,共88分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤) A B C D E (第19题图) 17.(5分)计算:. 18.(5分)先化简,再求值:,其中a=-2,b=. 19.(6分)如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AE∥BC, DE∥AB. 证明:(1)AE=DC;(2)四边形ADCE为矩形. 20.(6分)某区为了解全区2800名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分24分,得分均为整数),制成下表: 分数段(x分) x≤16 17≤x≤18 19≤x≤20 21≤x≤22 23≤x≤24 人 数 10 15 35 112 128 (1)填空:①本次抽样调查共抽取了 名学生;②学生成绩的中位数落在 分数段; ③若用扇形统计图表示统计结果,则分数段为x≤16的人数所对应扇形的圆心角为 °; (2)如果将21分以上(含21分)定为优秀,请估计该区九年级考生成绩为优秀的人数. 21.(6分)某初级中学准备随机选出七、八、九三个年级各1名学生担任领操员.现已知这三个年级分别选送一男、一女共6名学生为备选人.(1)请你利用树状图或表格列出所有可能的选法; (2)求选出“两男一女”三名领操员的概率. (第22题图) 调整前: 调整后: 调整方案: 加收1元燃油附加费,其它收费标准保持不变. 路程x/km 车费y/元 0 1 2 3 4 5 6 16 15 14 13 12 11 10 9 22.(6分)受国际原油价格持续上涨影响,某市对出租车的收费标准进行调整. . (1)调整前出租车的起步价为 元,超过3km收费 元/km; (2)求调整后的车费y(元)与行驶路程x(km)(x>3)之间的函数关系式,并在图中画出其函数图象. 23.(8分) 现有一张宽为12cm练习纸,相邻两条格线间的距离均为0.8cm.调皮的小聪在纸的左上角用印章印出一个矩形卡通图案,图案的顶点恰好在四条格线上(如图),测得∠α=32°. (1)求矩形图案的面积; (2)若小聪在第一个图案的右 边以同样的方式继续盖印 (如图),最多能印几个完整的图案? (参考数据: sin32°≈0.5,cos32°≈0.8, tan32°≈0.6) 0.8cm …… 12cm α (第23题图) 型 号 A B 进 价 1200元/部 1000元/部 售 价 1380元/部 1200元/部 24.(8分)某手机专营店代理销售A、B两种型号手机.手机的进价、售价如下表:(1)第一季度:用36000元购进 A、B两种型号的手机,全部售完后获利6300元, D B C A O (第25题图) (1)求第一季度购进A、B两种型号手机的数量; (2)第二季度:计划购进A、B两种型号手机共34部,且不超出第一季度的购机总费用,则A型号手机最多能购多少部? 25. (8分)如图,在△ABC中,AB=AC,点O为底边上的中点,以点O为圆心, 1为半径的半圆与边AB相切于点D. (1)判断直线AC与⊙O的位置关系,并说明理由; (2)当∠A=60°时,求图中阴影部分的面积. 26.(9分)已知二次函数的图象与x轴相交于A、B两点(A左B右),与y轴相交于点C,顶点为D. (1)求m的取值范围;(2)当点A的坐标为,求点B的坐标;(3)当BC⊥CD时,求m的值. 27.(9分) 操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计: 说明: 方案一图形中的圆过点A、B、C; 方案二直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点. A B C 方案一 方案二 纸片利用率=×100% 发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由. (2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程. 探究:(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率. 方案三 说明: 方案三中的每条边均过其中两个正方形的顶点. 28.(12分)如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一点,且AD=3cm,动点E从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为x s.作∠DEF=45°,与边BC相交于点F.设BF长为ycm. A B C D E F (第28题图) (第28题备用图) A B C D (1)当x= s时,DE⊥AB; (2)求在点E运动过程中,y与x之间的 函数关系式及点F运动路线的长; (3)当△BEF为等腰三角形时, 求x的值. 一、选择题(每小题2分,共计12分) 题号 1 2 3 4 5 6 答案 C C B B C A 二、填空题(每小题2分,共计20分) 7.1 8. 9.100 10. 11.2 12.24 13.3 14.x>1 15.18 16.2︰(或或) 三、解答题(本大题共12小题,共计88分) 17.(本题5分解:原式=1-2+3 3分 =-1+3 5分 18.(本题5分)解:原式 2分 3分 4分 A B C D E 当a=-2,b=1时,原式= = 5分 19.(本题6分) 证明:(1)在△ABC中,∵AB=AC,AD⊥BC, ∴BD=DC 1分 ∵AE∥BC, DE∥AB, ∴四边形ABDE为平行四边形 2分 ∴BD=AE, 3分 ∵BD=DC ∴AE = DC. 4分 (2)解法一:∵AE∥BC,AE = DC, ∴四边形ADCE为平行四边形. 5分 又∵AD⊥BC, ∴∠ADC=90°, ∴四边形ADCE为矩形. 6分 解法二:∵AE∥BC,AE = DC, ∴四边形ADCE为平行四边形 5分 又∵四边形ABDE为平行四边形 ∴AB=DE.∵AB=AC,∴DE=AC. ∴四边形ADCE为矩形. 6分 20.(本题6分)解法一:(1)用表格列出所有可能结果: 七年级 八年级 九年级 结果 男 男 男 (男,男,男) 男 男 女 (男,男,女) 男 女 男 (男,女,男) 男 女 女 (男,女,女) 女 女 女 (女,女,女) 女 女 男 (女,女,男) 女 男 女 (女,男,女) 女 男 男 (女,男,男) 3分 (2)从上表可知:共有8种结果,且每种结果都是等可能的,其中“两男一女”的结果有3种. 5分 所以,P(两男一女)=. 6分 解法二:(1)用树状图列出所有可能结果: (男,男,男) (男,男,女) 男 女 男 (男,女,男) (男,女,女) 男 女 (女,男,男) (女,男,女) 男 女 男 (女,女,男) (女,女,女) 男 女 女 男 女 开始 七年级 八年级 九年级 结果 3分 (2)从上图可知:共有8种结果,且每种结果都是等可能的,其中“两男一女”的结果有3种. 5分 所以,P(两男一女)=. 6分 21.(本题6分)(1)①300 1分 ②21≤x≤22 3分 ③12 4分 (2)2800×=2240(人) 5分 答:该区所有学生中口语成绩为满分的人数约为2240人. 6分 22.(本题6分)解:(1)9;2.5; 2分 (2)y=10+2.5(x-3)=2.5x+2.5 5分 调整后的图像如图: 调整前: 调整后: 路程x/km 车费y/元 0 1 2 3 4 5 6 16 15 14 13 12 11 10 9 6分 23.(本题8分) (1)如图,在Rt△BCE中, ∵sinα=,∴BC = = = 1.6 2分 ∵矩形ABCD中,∴∠BCD=90°,∴∠BCE+∠FCD=90°, 又∵在Rt△BCE中,∴∠EBC+∠BCE=90°,∴∠FCD=32°. 在Rt△FCD中,∵cos∠FCD=,∴CD===2 4分 E …… 0.8cm 12cm α B A C D F G H ∴橡皮的长和宽分别为2cm和1.6cm. (2)如图,在Rt△ADH中,易求得∠DAH=32°.∵cos∠DAH=, ∴AH===2 5分 在Rt△CGH中,∠GCH=32°.∵tan∠GCH=, ∴GH=CG tan32°= 0.8×0.6 = 0.48 7分 又∵6×2+0.48>12,5×2+0.48<12,3×4+0.9616,∴最多能摆放5块橡皮. 8分 24.(本题8分) (1)解:设该专营店第一季度购进A、B两种型号手机的数量分别为x部和y部. 1分 由题意可知: 3分 解得: 答:该专营店本次购进A、B两种型号手机的数分别为15部和18部. 4分 (2)解:设第二季度购进A型号手机a部. 5分 由题意可知:1200a+1000(34-a)≤36000, 6分 解得:a≤10 7分 E D B C A O ● ● 不等式的最大整数解为10 答:第二季度最多能购A型号手机10部. 8分 25.(本题8分) 解:(1)直线AC与⊙O相切. 1分 理由是: 连接OD,过点O作OE⊥AC,垂足为点E. ∵⊙O与边AB相切于点D, ∴OD⊥AB. 2分 ∵AB=AC,点O为底边上的中点, ∴AO平分∠BAC 3分 又∵OD⊥AB,OE⊥AC ∴OD= OE 4分 ∴OE是⊙O的半径. 又∵OE⊥AC,∴直线AC与⊙O相切. 5分 (2)∵AO平分∠BAC,且∠BAC=60°, ∴∠OAD=∠OAE=30°, ∴∠AOD=∠AOE=60°, 在Rt△OAD中,∵tan∠OAD = ,∴AD==,同理可得AE= ∴S四边形ADOE =×OD×AD×2=×1××2= 6分 又∵S扇形形ODE==π 7分 ∴S阴影= S四边形ADOE -S扇形形ODE=-π. 8分 26.(本题9分) 解:(1)∵二次函数的图象与x轴相交于A、B两点 ∴b2-4ac>0,∴4+4m>0, 2分 解得:m>-1 3分 (2)解法一: ∵二次函数的图象的对称轴为直线x=-=1 4分 ∴根据抛物线的对称性得点B的坐标为(5,0) 6分 解法二: 把x=-3,y=0代入中得m=15 4分 ∴二次函数的表达式为 令y=0得 5分 O y x A B C D E 解得x1=-3,x2=5 ∴点B的坐标为(5,0) 6分 (3)如图,过D作DE⊥y轴,垂足为E.∴∠DEC=∠COB=90°, 当BC⊥CD时,∠DCE +∠BCO=90°, ∵∠DEC=90°,∴∠DCE +∠EDC=90°,∴∠EDC=∠BCO. ∴△DEC∽△COB,∴=. 7分 由题意得:OE=m+1,OC=m,DE=1,∴EC=1.∴ =. ∴OB=m,∴B的坐标为(m,0). 8分 将(m,0)代入得:-m 2+2 m + m=0. 解得:m1=0(舍去), m2=3. 9分 27.(本题9分) 发现:(1)小明的这个发现正确. 1分 理由:解法一:如图一:连接AC、BC、AB,∵AC=BC=,AB= ∴AC2+BC2=AB2 ∴∠BAC=90°, 2分 ∴AB为该圆的直径. 3分 解法二:如图二:连接AC、BC、AB.易证△AMC≌△BNC,∴∠ACM=∠CBN. 又∵∠BCN+∠CBN=90°,∴∠BCN+∠ACM=90°,即∠BAC=90°, 2分 ∴AB为该圆的直径. 3分 C B A D E F H 图三 图一 M 图二 N (2)如图三:易证△ADE≌△EHF,∴AD=EH=1. 4分 ∵DE∥BC,∴△ADE∽△ACB,∴=∴=,∴BC=8. 5分 ∴S△ACB=16. 6分 ∴该方案纸片利用率=×100%=×100%=37.5% 7分 探究:(3) 9分 28.(本题12分)解:(1) 2分 (2)∵在△ABC中,∠C=90°,AC=BC=4. ∴∠A=∠B=45°,AB=4,∴∠ADE+∠AED=135°; 又∵∠DEF=45°,∴∠BEF+∠AED=135°,∴∠ADE=∠BEF; ∴△ADE∽△BEF 4分 ∴=, ∴=,∴y=-x2+x 5分 ∴y=-x2+x=-( x-2)2+ ∴当x=2时,y有最大值= 6分 ∴点F运动路程为cm 7分 A B C D E F 第28题(1)(2)图 A B C D E F 第28题(3)①图 (3)这里有三种情况: ①如图,若EF=BF,则∠B=∠BEF; 又∵△ADE∽△BEF,∴∠A=∠ADE=45° ∴∠AED=90°,∴AE=DE=, ∵动点E的速度为1cm/s ,∴此时x=s; ②如图,若EF=BE,则∠B=∠EFB; 又∵△ADE∽△BEF,∴∠A=∠AED=45° ∴∠ADE=90°,∴AE=3, ∵动点E的速度为1cm/s ∴此时x=3s; A B C D E F 第28题(3)②图 A B C D E F 第28题(3)③图 ③如图,若BF=BE,则∠FEB=∠EFB; 又∵△ADE∽△BEF,∴∠ADE=∠AED ∴AE=AD=3, ∵动点E的速度为1cm/s ∴此时x=3s; 综上所述,当△BEF为等腰三角形时,x的值为s或3s或3s. (注:求对一个结论得2分,求对两个结论得4分,求对三个结论得5分)查看更多