- 2021-05-10 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
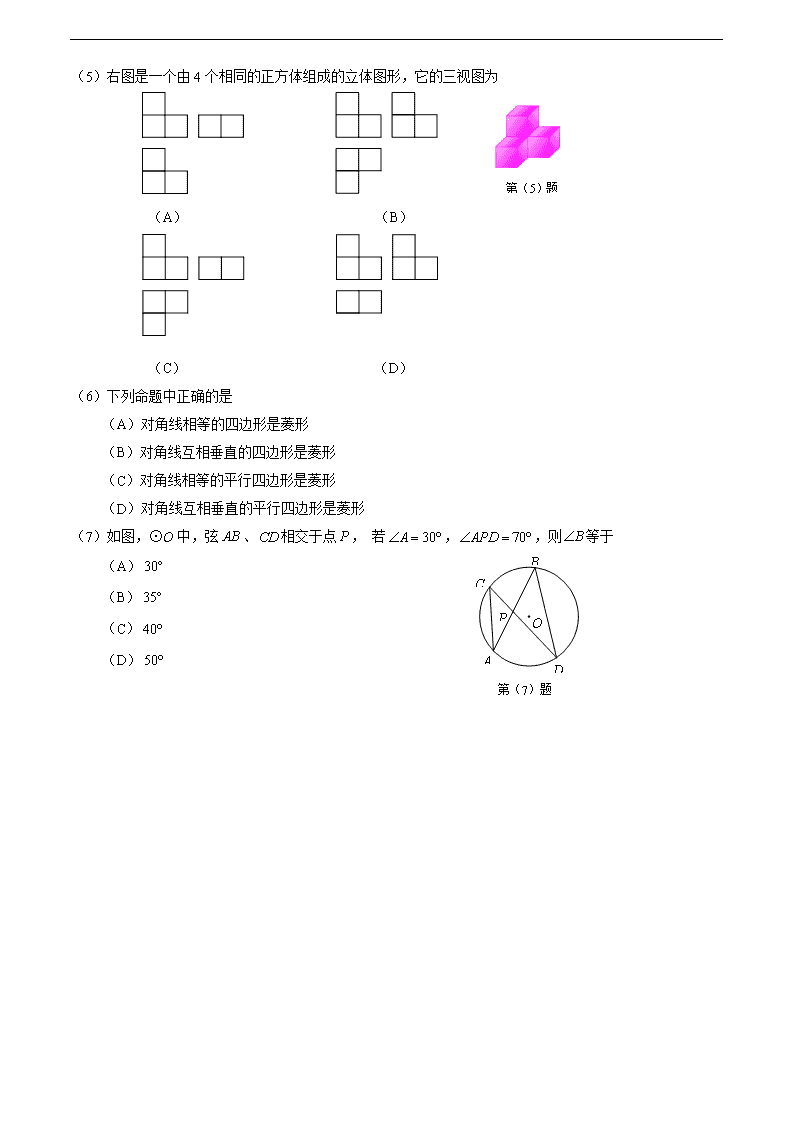
2010年天津市初中毕业生学业考试试卷
2010年天津市初中毕业生学业考试试卷 数 学 本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。第Ⅰ卷第1页至第3页,第Ⅱ卷第4页至第8页。试卷满分120分。考试时间100分钟。 答卷前,考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上,并在规定位置粘贴考试用条形码。答题时,务必将答案涂写在“答题卡”上,答案答在试卷上无效。考试结束后,将本试卷和“答题卡”一并交回。 祝各位考生考试顺利! 第Ⅰ卷(选择题 共30分) 注意事项: 每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。 一、 选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的. (1)的值等于 (A) (B) (C) (D)1 (2)下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为 (A) (B) (C) (D) (3)上海世博会是我国第一次举办的综合类世界博览会.据统计自2010年5月1日开 幕至5月31日,累计参观人数约为8 030 000人,将8 030 000用科学记数法表示 应为 (A) (B) (C) (D) (4)在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是7环,其中甲的成绩的方差为1.21,乙的成绩的方差为3.98,由此可知 (A)甲比乙的成绩稳定 (B)乙比甲的成绩稳定 (C)甲、乙两人的成绩一样稳定 (D)无法确定谁的成绩更稳定 (5)右图是一个由4个相同的正方体组成的立体图形,它的三视图为 第(5)题 (A) (B) (C) (D) (6)下列命题中正确的是 (A)对角线相等的四边形是菱形 (B)对角线互相垂直的四边形是菱形 (C)对角线相等的平行四边形是菱形 (D)对角线互相垂直的平行四边形是菱形 第(7)题 B C A D P O (7)如图,⊙O中,弦、相交于点, 若,,则等于 (A) (B) (C) (D) (8)比较2,,的大小,正确的是 (A) (B) (C) (D) (9)如图,是一种古代计时器——“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间.若用表示时间,表示壶底到水面的高度,下面的图象适合表示一小段时间内与的函数关系的是(不考虑水量变化对压力的影响) 第(9)题 y O x y O x y O x y O x (A) (B) (C) (D) (10)已知二次函数()的图象如图所示,有下列结论: 第(10)题 y x O ①; ②; ③; ④. 其中,正确结论的个数是 (A)1 (B)2 (C)3 (D)4 2010年天津市初中毕业生学业考试试卷 数 学 第Ⅱ卷(非选择题 共90分) 注意事项: 用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。 二、填空题:本大题共8小题,每小题3分,共24分. 第(13)题 A C D B E F (11)若,则的值为 . (12)已知一次函数与的图象交于点, 则点的坐标为 . 第(14)题 E A D B C (13)如图,已知,,点A、D、B、F在一 条直线上,要使△≌△,还需添加一个条件, 这个条件可以是 . (14)如图,已知正方形的边长为3,为边上一点, .以点为中心,把△顺时针旋转,得 △,连接,则的长等于 . (15)甲盒装有3个乒乓球,分别标号为1,2,3;乙盒装有2个乒乓球,分别标号为 1,2.现分别从每个盒中随机地取出1个球,则取出的两球标号之和为4的概率是 . (16)已知二次函数()中自变量和函数值的部分对应值如下表: … 0 1 … … 0 … 第(17)题 D C A F B E G 则该二次函数的解析式为 . (17)如图,等边三角形中,、分别为、边上 的点,,与交于点,于点, 则的值为 . (18)有一张矩形纸片ABCD,按下面步骤进行折叠: 第一步:如图①,将矩形纸片折叠,使点B、D重合,点C落在点处,得折痕EF; 第二步:如图②,将五边形折叠,使AE、重合,得折痕DG,再打开; 第三步:如图③,进一步折叠,使AE、均落在DG上,点A、落在点处,点E、F落在点处,得折痕MN、QP. 第(18)题 A D C B E F G A D C B E F 图① 图② 图③ D F C A E N P B M Q G 这样,就可以折出一个五边形. (Ⅰ)请写出图①中一组相等的线段 (写出一组即可); (Ⅱ)若这样折出的五边形DMNPQ(如图③)恰好是一个正五边形,当,,时,有下列结论: ①; ②; ③; ④. 其中,正确结论的序号是 (把你认为正确结论的序号都填上). 三、解答题:本大题共8小题,共66分.解答应写出文字说明、演算步骤或证明过程. (19)(本小题6分) 解不等式组 (20)(本小题8分) 已知反比例函数(为常数,). (Ⅰ)若点在这个函数的图象上,求的值; (Ⅱ)若在这个函数图象的每一支上,随的增大而减小,求的取值范围; (Ⅲ)若,试判断点,是否在这个函数的图象上,并说明理由. (21)(本小题8分) 第(21)题 户数 月均用水量/t 1 2 3 4 0 6 6.5 7 7.5 8 我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图. (Ⅰ)求这10个样本数据的平均数、众数和中位数; (Ⅱ)根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户. (22)(本小题8分) 已知是⊙的直径,是⊙的切线,是切点,与⊙交于点. (Ⅰ)如图①,若,,求的长(结果保留根号); A B C O P 图① A B C O P D 图② 第(22)题 (Ⅱ)如图②,若为的中点,求证直线是⊙的切线. (23)(本小题8分) A B C D 45° 60° 第(23)题 永乐桥摩天轮是天津市的标志性景观之一.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C处测得摩天轮的最高点A的仰角为,再往摩天轮的方向前进50 m至D处,测得最高点A的仰角为. 求该兴趣小组测得的摩天轮的高度AB(, 结果保留整数). (24)(本小题8分) 注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答. 青山村种的水稻2007年平均每公顷产8 000 kg,2009年平均每公顷产9 680 kg,求该村水稻每公顷产量的年平均增长率. 解题方案: 设该村水稻每公顷产量的年平均增长率为. (Ⅰ)用含的代数式表示: ① 2008年种的水稻平均每公顷的产量为 ; ② 2009年种的水稻平均每公顷的产量为 ; (Ⅱ)根据题意,列出相应方程 ; (Ⅲ)解这个方程,得 ; (Ⅳ)检验: ; (Ⅴ)答:该村水稻每公顷产量的年平均增长率为 %. (25)(本小题10分) 在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在轴、 轴的正半轴上,,,D为边OB的中点. 温馨提示:如图,可以作点D关于轴的对称点,连接与轴交于点E,此时△的周长是最小的.这样,你只需求出的长,就可以确定点的坐标了. (Ⅰ)若为边上的一个动点,当△的周长最小时,求点的坐标; 第(25)题 y B O D C A x E y B O D C A x (Ⅱ)若、为边上的两个动点,且,当四边形的周长最小时,求点、的坐标. (26)(本小题10分) 在平面直角坐标系中,已知抛物线与轴交于点、(点在点的左侧),与轴的正半轴交于点,顶点为. (Ⅰ)若,,求此时抛物线顶点的坐标; (Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足 S△BCE = S△ABC,求此时直线的解析式; (Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足 S△BCE = 2S△AOC,且顶点恰好落在直线上,求此时抛物线的解析式. 2010年天津市初中毕业生学业考试 数学试题参考答案及评分标准 评分说明: 1.各题均按参考答案及评分标准评分。 2.若考生的非选择题答案与参考答案不完全相同但言之有理,可酌情评分,但不得超过该题所分配的分数。 一、选择题:本大题共10小题,每小题3分,共30分. (1)A (2)B (3)C (4)A (5)B (6)D (7)C (8)C (9)B (10)D 二、填空题:本大题共8小题,每小题3分,共24分. (11) (12)(3,0) (13)(答案不惟一,也可以是或) (14) (15) (16) (17) (18)(Ⅰ)(答案不惟一,也可以是等);(Ⅱ)①②③ 三、解答题:本大题共8小题,共66分. (19)(本小题6分) ① ② 解: ∵ 解不等式①,得. ……………………………………… 2分 解不等式②,得. ……………………………………… 4分 ∴ 原不等式组的解集为. ……………………………………… 6分 (20)(本小题8分) 解:(Ⅰ)∵ 点在这个函数的图象上, ∴ .解得. ..............................2分 (Ⅱ)∵ 在函数图象的每一支上,随的增大而减小, ∴ .解得. ..............................4分 (Ⅲ)∵ ,有. ∴ 反比例函数的解析式为. 将点的坐标代入,可知点的坐标满足函数关系式, ∴ 点在函数的图象上. 将点的坐标代入,由,可知点的坐标不满足函数关系式, ∴ 点不在函数的图象上. ..............................8分 (21)(本小题8分) 解:(Ⅰ)观察条形图,可知这组样本数据的平均数是 . ∴ 这组样本数据的平均数为. ∵ 在这组样本数据中,出现了4次,出现的次数最多, ∴ 这组数据的众数是. ∵ 将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是, 有 , ∴ 这组数据的中位数是. ..............................6分 (Ⅱ)∵ 10户中月均用水量不超过7 t的有7户, 有 . ∴ 根据样本数据,可以估计出小刚所在班50名同学家庭中月均用水量不超过7 t的约有35户. ..............................8分 (22)(本小题8分) 解:(Ⅰ)∵ 是⊙的直径,是切线, ∴ . 在Rt△中,,, ∴ . 由勾股定理,得. ..................5分 (Ⅱ)如图,连接、, A B C O P D ∵ 是⊙的直径, ∴ ,有. 在Rt△中,为的中点, ∴ . ∴ . 又 ∵, ∴. ∵ , ∴ . 即 . ∴ 直线是⊙的切线. ..............................8分 (23)(本小题8分) 解:根据题意,可知,,. 在Rt△中,由,得. 在Rt△中,由, 得. ..............................6分 又 ∵ , ∴ ,即. ∴ . 答:该兴趣小组测得的摩天轮的高度约为118 m. .....................8分 (24)(本小题8分) 解:(Ⅰ)①;②; (Ⅱ); ........................4分 (Ⅲ),; (Ⅳ),都是原方程的根,但不符合题意,所以只取; (Ⅴ)10 . ........................8分 (25)(本小题10分) 解:(Ⅰ)如图,作点D关于轴的对称点,连接与轴交于点E,连接. 若在边上任取点(与点E不重合),连接、、. y B O D C A x E 由, 可知△的周长最小. ∵ 在矩形中,,,为的中点, ∴ ,,. ∵ OE∥BC, ∴ Rt△∽Rt△,有. ∴ . ∴ 点的坐标为(1,0). ................................6分 y B O D C A x E G F (Ⅱ)如图,作点关于轴的对称点,在边上截取,连接与轴交于点,在上截取. ∵ GC∥EF,, ∴ 四边形为平行四边形,有. 又 、的长为定值, ∴ 此时得到的点、使四边形的周长最小. ∵ OE∥BC, ∴ Rt△∽Rt△, 有 . ∴ . ∴ . ∴ 点的坐标为(,0),点的坐标为(,0). ...............10分 (26)(本小题10分) 解:(Ⅰ)当,时,抛物线的解析式为,即. ∴ 抛物线顶点的坐标为(1,4). .................2分 (Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点在对称轴上,有, ∴ 抛物线的解析式为(). ∴ 此时,抛物线与轴的交点为,顶点为. ∵ 方程的两个根为,, ∴ 此时,抛物线与轴的交点为,. E y x F B D A O C 如图,过点作EF∥CB与轴交于点,连接,则S△BCE = S△BCF. ∵ S△BCE = S△ABC, ∴ S△BCF = S△ABC. ∴ . 设对称轴与轴交于点, 则. 由EF∥CB,得. ∴ Rt△EDF∽Rt△COB.有. ∴ .结合题意,解得 . ∴ 点,. 设直线的解析式为,则 解得 ∴ 直线的解析式为. .........................6分 (Ⅲ)根据题意,设抛物线的顶点为,(,) 则抛物线的解析式为, 此时,抛物线与轴的交点为, 与轴的交点为,.() 过点作EF∥CB与轴交于点,连接, 则S△BCE = S△BCF. 由S△BCE = 2S△AOC, ∴ S△BCF = 2S△AOC. 得. 设该抛物线的对称轴与轴交于点. 则 . 于是,由Rt△EDF∽Rt△COB,有. ∴ ,即. 结合题意,解得 . ① ∵ 点在直线上,有. ② ∴ 由①②,结合题意,解得. 有,. ∴ 抛物线的解析式为. .........................10分查看更多