中考数学压轴题练习正方形问题

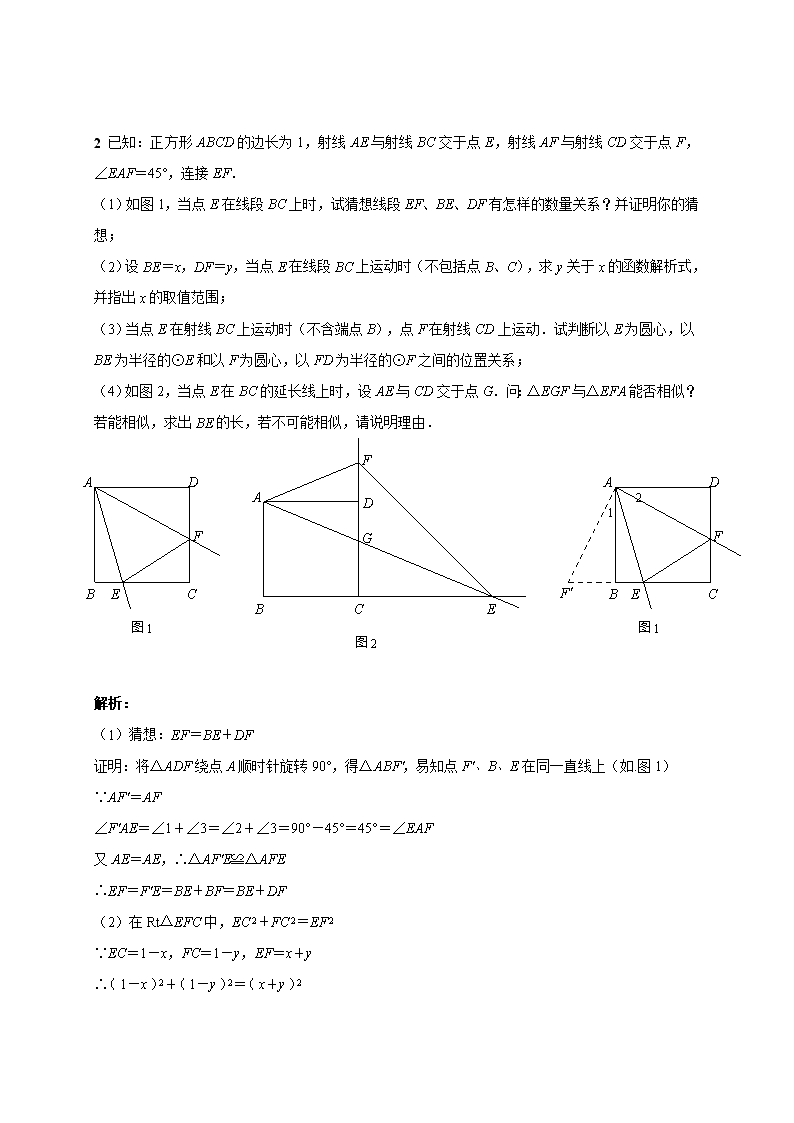
中考数学压轴题练习正方形问题

N K G C E D F A B P M ‎1 如图，在边长为6的正方形ABCD的两侧作正方形BEFG和正方形DMNK，恰好使得N、A、F三点在一直线上，连接MF交线段AD于点P，连接NP，设正方形BEFG的边长为x，正方形DMNK的边长为y．‎ ‎（1）求y关于x的函数关系式及自变量x的取值范围；‎ ‎（2）当△NPF的面积为32时，求x的值；‎ ‎（3）以P为圆心，AP为半径的圆能否与以G为圆心，GF为半径的圆相切？如果能，请求出x的值，如果不能，请说明理由．‎ 解析：（1）∵正方形BEFG、正方形DMNK、正方形ABCD ‎∴∠E＝∠F＝90O ，AE∥MC，MC∥NK ‎∴AE∥NK，∴∠KNA＝∠EAF ‎∴△KNA∽△EAF，∴ ＝ ，即 ＝ ‎∴y＝x＋6（0＜x ≤6）‎ ‎（2）由（1）知NK＝AE，∴AN＝AF ‎∵正方形DMNK，∴AP∥NM，∴ ＝ ＝1‎ ‎∴FP＝PM，∴S△MNP ＝S△NPF ＝32‎ ‎∴S正方形DMNK ＝2S△MNP ＝64‎ ‎∴y＝8，∴x＝2‎ ‎（3）连接PG，延长FG交AD于点H，则GH⊥AD 易知：AP＝ ，AH＝x，PH＝ －x，HG＝6；PG＝AP＋GF＝ ＋x ‎①当两圆外切时 在Rt△GHP中，PH 2＋HG 2＝PG 2，即( －x )2＋6 2＝( ＋x )2‎ 解得：x＝－3－3 （舍去）或x＝－3＋3 ‎②当两圆内切时 在Rt△GHP中，PH 2＋HG 2＝PG 2，即( －x )2＋6 2＝( －x )2‎ 方程无解 所以，当x＝3 －3时，两圆相切 ‎2 已知：正方形ABCD的边长为1，射线AE与射线BC交于点E，射线AF与射线CD交于点F，∠EAF＝45°，连接EF．‎ ‎（1）如图1，当点E在线段BC上时，试猜想线段EF、BE、DF有怎样的数量关系？并证明你的猜想；‎ ‎（2）设BE＝x，DF＝y，当点E在线段BC上运动时（不包括点B、C），求y关于x的函数解析式，并指出x的取值范围；‎ ‎（3）当点E在射线BC上运动时（不含端点B），点F在射线CD上运动．试判断以E为圆心，以BE为半径的⊙E和以F为圆心，以FD为半径的⊙F之间的位置关系；‎ ‎（4）如图2，当点E在BC的延长线上时，设AE与CD交于点G．问：△EGF与△EFA能否相似？若能相似，求出BE的长，若不可能相似，请说明理由．‎ A B D C E F G 图2‎ A B D C E F 图1‎ F′‎ ‎1‎ ‎2‎ A B D C E F 图1‎ 解析：‎ ‎（1）猜想：EF＝BE＋DF 证明：将△ADF绕点A顺时针旋转90°，得△ABF′，易知点F′、B、E在同一直线上（如.图1）‎ ‎∵AF′＝AF ‎∠F′AE＝∠1＋∠3＝∠2＋∠3＝90°－45°＝45°＝∠EAF 又AE＝AE，∴△AF′E≌△AFE ‎∴EF＝F′E＝BE＋BF＝BE＋DF ‎（2）在Rt△EFC中，EC 2＋FC 2＝EF 2‎ ‎∵EC＝1－x，FC＝1－y，EF＝x＋y ‎∴( 1－x )2＋( 1－y )2＝( x＋y )2‎ ‎∴y＝ （0＜x ＜1）‎ ‎（3）①当点E在点B、C之间时，由（1）知EF＝BE＋DF，故此时⊙E与⊙F外切；‎ ‎②当点E在点C时，DF＝0，⊙F不存在.‎ ‎③当点E在BC延长线上时，将△ADF绕点A顺时针旋转90°，得△ABF′（如图2）‎ 则AF′＝AF，∠1＝∠2，BF′＝DF，∠F′AF＝90°‎ ‎∴∠F′AE＝∠EAF＝45°‎ 又AE＝AE，∴△AF′E≌△AFE ‎∴EF＝EF′＝BE－BF′＝BE－DF ‎∴此时⊙E与⊙F内切 综上所述，当点E在线段BC上时，⊙E与⊙F外切；当点E在BC延长线上时，⊙E与⊙F内切 A B D C E F G 图2‎ F′‎ ‎1‎ ‎2‎ ‎（4）△EGF与△EFA能够相似，只要当∠EFG＝∠EAF＝45° 即可 此时CE＝CF 设BE＝x，DF＝y，由（3）知EF＝x－y 在Rt△CFE中，CE 2＋CF 2＝EF 2‎ ‎∴( x－1 )2＋( 1＋y )2＝( x－y )2‎ ‎∴y＝ （x ＞1）‎ 由CE＝CF，得x－1＝1＋y，即x－1＝1＋ 化简得x 2－2x－1＝0，解得x1＝1－ （舍去），x2＝1＋ ‎∴△EGF与△EFA能够相似，此时BE的长为1＋ ‎3 已知：如图，在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝2，BC＝6，AB＝3．E为BC边上一点，以BE为边作正方形BEFG，使正方形BEFG和梯形ABCD在BC的同侧．‎ ‎（1）当正方形的顶点F恰好落在对角线AC上时，求BE的长；‎ ‎（2）将（1）问中的正方形BEFG沿BC向右平移，记平移中的正方形BEFG为正方形B′EFG，当点E与点C重合时停止平移．设平移的距离为t，正方形B′EFG的边EF与AC交于点M，连接B′D，B′M，DM．是否存在这样的t，使△B′DM是直角三角形？若存在，求出t的值；若不存在，请说明理由；‎ ‎（3）在（2）问的平移过程中，设正方形B′EFG与△ADC重叠部分的面积为S，请直接写出S与t 之间的函数关系式以及自变量t的取值范围．‎ B A C D 备用图 B A C D 解析：（1）如图①，设正方形BEFG的边长为x 则BE＝FG＝BG＝x B A C D 图①‎ E F G ‎∵AB＝3，BC＝6，∴AG＝AB－BG＝3－x ‎∵GF∥BE，∴△AGF∽△ABC ‎∴ ＝ ，即 ＝ 解得x＝2，即BE＝2‎ ‎（2）存在满足条件的t，理由如下：‎ 如图②，过D作DH⊥BC于点H 则BH＝AD＝2，DH＝AB＝3‎ 由题意得：BB′＝HE＝t，HB′＝|t－2|，EC＝4－t B A C D 图②‎ E F G H B′‎ M N 在Rt△B′ME中，B′M 2＝B′E 2＋ME 2＝2 2＋( 2－ t )2＝ t 2－2t＋8‎ ‎∵EF∥AB，∴△MEC∽△ABC ‎∴ ＝ ，即 ＝ ，∴ME＝2－ t 在Rt△DHB′ 中，B′D 2＝DH 2＋B′H 2＝3 2＋( t－2 )2＝t 2－4t＋13‎ 过M作MN⊥DH于点N 则MN＝HE＝t，NH＝ME＝2－ t ‎∴DN＝DH－NH＝3－( 2－ t )＝ t＋1‎ 在Rt△DMN中，DM 2＝DN 2＋MN 2＝ t 2＋t＋1‎ ‎（ⅰ）若∠DB′M＝90°，则DM 2＝B′M 2＋B′D 2‎ 即 t 2＋t＋1＝( t 2－2t＋8 )＋( t 2－4t＋13 )，解得t＝ ‎（ⅱ）若∠B′MD＝90°，则B′D 2＝B′M 2＋DM 2‎ 即t 2－4t＋13＝( t 2－2t＋8 )＋( t 2＋t＋1 )，解得t1＝－3＋ ，t2＝－3－ ‎∵0≤t ≤4，∴t＝－3＋ ‎（ⅲ）若∠B′DM＝90°，则B′M 2＝B′D 2＋DM 2‎ 即 t 2－2t＋8＝( t 2－4t＋13 )＋( t 2＋t＋1 )，此方程无解 B A C D 图③‎ E F G B′‎ H 综上所述，当t＝ 或－3＋ 时，△B′DM是直角三角形 ‎（3）当0≤t ≤ 时，S＝ t 2‎ 当 ≤t ≤2时，S＝－ t 2＋t－ 当2≤t ≤ 时，S＝－ t 2＋2t－ B A C D 图④‎ E F G B′‎ H 当 ≤t ≤4时，S＝－ t＋ 提示：‎ 当点F落在CD上时，如图③‎ FE＝2，EC＝4－t，DH＝3，HC＝4‎ 由△FEC∽△DHC，得 ＝ 即 ＝ ，∴t＝ 当点G落在AC上时，点G也在DH上（即DH与AC的交点）‎ B A C D 图⑤‎ E F G B′‎ M N t＝2‎ 当点G落在CD上时，如图④‎ GB′＝2，B′C＝6－t 由△GB′C∽△DHC，得 ＝ 即 ＝ ，∴t＝ 当点E与点C重合时，t＝4‎ B A C D 图⑥‎ E F G B′‎ M N P Q ‎①当0≤t ≤ 时，如图⑤‎ ‎∵MF＝t，FN＝ t ‎∴S＝S△FMN ＝ ·t· t＝ t 2‎ ‎②当 ≤t ≤2时，如图⑥‎ ‎∵PF＝t－ ，FQ＝ PF＝ t－1‎ B A C D 图⑦‎ E F G B′‎ P Q M N ‎∴S△FPQ ＝ ( t－ )( t－1 )＝ t 2－t＋ ‎∴S＝S△FMN －S△FPQ ＝ t 2－( t 2－t＋ )＝－ t 2＋t－ ‎③当2≤t ≤ 时，如图⑦‎ ‎∵B′M＝ B′C＝ ( 6－t )＝3－ t ‎∴GM＝2－( 3－ t )＝ t－1‎ ‎∴S梯形GMNF ＝ ( t－1＋ t )×2＝t－1‎ ‎∴S＝S梯形GMNF －S△FPQ ＝( t－1 )－( t 2－t＋ )＝－ t 2＋2t－ B A C D 图⑧‎ E F G B′‎ P Q N M ‎④当 ≤t ≤4时，如图⑧‎ ‎∵PB′＝ B′C＝ ( 6－t )＝ － t ‎∴GP＝2－( － t )＝ t－ ‎∴S梯形GPQF ＝ ( t－ ＋ t－1 )×2＝ t－ ‎∴S＝S梯形GMNF －S梯形GPQF ＝( t－1 )－( t－ )＝－ t＋