中考数学易错题目综合专题目四

中考数学易错题目综合专题目四

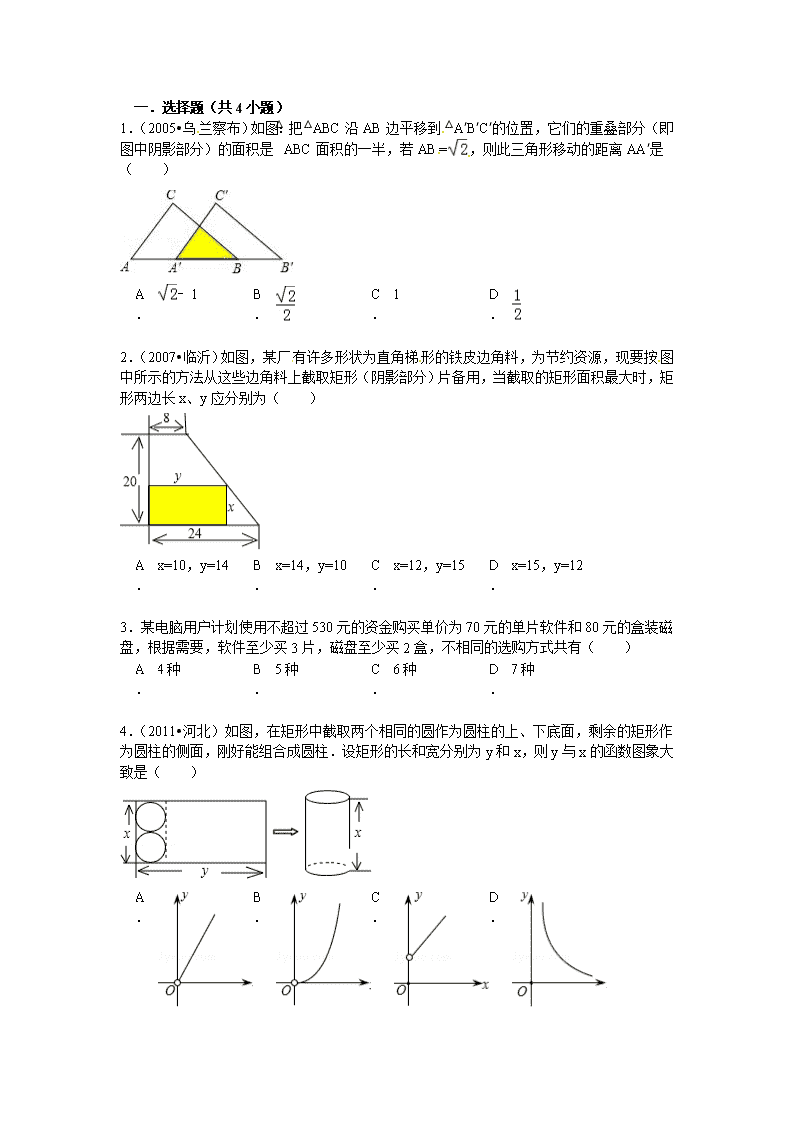
‎　一．选择题（共4小题）‎ ‎1．（2005•乌兰察布）如图：把△ABC沿AB边平移到△A′B′C′的位置，它们的重叠部分（即图中阴影部分）的面积是△ABC面积的一半，若AB=，则此三角形移动的距离AA′是（　　）‎ ‎　‎ A．‎ ‎﹣1‎ B．‎ C．‎ ‎1‎ D．‎ ‎　‎ ‎2．（2007•临沂）如图，某厂有许多形状为直角梯形的铁皮边角料，为节约资源，现要按图中所示的方法从这些边角料上截取矩形（阴影部分）片备用，当截取的矩形面积最大时，矩形两边长x、y应分别为（　　）‎ ‎　‎ A．‎ x=10，y=14‎ B．‎ x=14，y=10‎ C．‎ x=12，y=15‎ D．‎ x=15，y=12‎ ‎　‎ ‎3．某电脑用户计划使用不超过530元的资金购买单价为70元的单片软件和80元的盒装磁盘，根据需要，软件至少买3片，磁盘至少买2盒，不相同的选购方式共有（　　）‎ ‎　‎ A．‎ ‎4种 B．‎ ‎5种 C．‎ ‎6种 D．‎ ‎7种 ‎　‎ ‎4．（2011•河北）如图，在矩形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长和宽分别为y和x，则y与x的函数图象大致是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎　‎ 二．填空题（共2小题）‎ ‎5．二次函数y=ax2+bx+c若满足a﹣b+c=0，则其图象必经过点　_________　．‎ ‎　‎ ‎6．（2011•重庆）某步行街摆放有若干盆甲、乙、丙三种造型的盆景．甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成，乙种盆景由10朵红花和12朵黄花搭配而成，丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成．这些盆景一共用了2900朵红花，3750朵紫花，则黄花一共用了　_________　朵．‎ ‎　‎ ‎2013年5月402969905的初中数学组卷 参考答案与试题解析 ‎　‎ 一．选择题（共4小题）‎ ‎1．（2005•乌兰察布）如图：把△ABC沿AB边平移到△A′B′C′的位置，它们的重叠部分（即图中阴影部分）的面积是△ABC面积的一半，若AB=，则此三角形移动的距离AA′是（　　）‎ ‎　‎ A．‎ ‎﹣1‎ B．‎ C．‎ ‎1‎ D．‎ 考点：‎ 相似三角形的判定与性质；平移的性质．2611678‎ 分析：‎ 利用相似三角形面积的比等于相似比的平方先求出A′B，再求AA′就可以了．‎ 解答：‎ 解：设BC与A′C′交于点E，‎ 由平移的性质知，AC∥A′C′‎ ‎∴△BEA′∽△BCA ‎∴S△BEA′：S△BCA=A′B2：AB2=1：2‎ ‎∵AB=‎ ‎∴A′B=1‎ ‎∴AA′=AB﹣A′B=﹣1‎ 故选A．‎ 点评：‎ 本题利用了相似三角形的判定和性质及平移的性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．‎ ‎　‎ ‎2．（2007•临沂）如图，某厂有许多形状为直角梯形的铁皮边角料，为节约资源，现要按图中所示的方法从这些边角料上截取矩形（阴影部分）片备用，当截取的矩形面积最大时，矩形两边长x、y应分别为（　　）‎ ‎　‎ A．‎ x=10，y=14‎ B．‎ x=14，y=10‎ C．‎ x=12，y=15‎ D．‎ x=15，y=12‎ 考点：‎ 二次函数的应用．2611678‎ 专题：‎ 应用题．‎ 分析：‎ 由直角三角形相似得 ，得x=•（24﹣y），化简矩形面积S=xy的解析式为S=﹣（y﹣12）2+180，再利用二次函数的性质求出S 的最大值，以及取得最大值时x、y的值．‎ 解答：‎ 解：以直角梯形的下底直角边端点为原点，两直角边方向为x，y轴建立直角坐标系，过点D作DE⊥x轴于点E，‎ ‎∵NH∥DE，‎ ‎∴△CNH∽△CDE，‎ ‎∴=，‎ ‎∵CH=24﹣y，CE=24﹣8，DE=OA=20，NH=x，‎ ‎∴，得x=•（24﹣y），‎ ‎∴矩形面积S=xy=﹣（y﹣12）2+180，‎ ‎∴当y=12时，S有最大值，此时x=15．‎ 故选D．‎ 点评：‎ 本题考查的是直角梯形以及矩形的性质的相关知识点．‎ ‎　‎ ‎3．某电脑用户计划使用不超过530元的资金购买单价为70元的单片软件和80元的盒装磁盘，根据需要，软件至少买3片，磁盘至少买2盒，不相同的选购方式共有（　　）‎ ‎　‎ A．‎ ‎4种 B．‎ ‎5种 C．‎ ‎6种 D．‎ ‎7种 考点：‎ 一元一次不等式组的应用．2611678‎ 专题：‎ 应用题．‎ 分析：‎ 本题先由题意找出不等关系列出不等式组为得：，解出即可．‎ 解答：‎ 解：设买软件x片，磁盘y盒，x取正整数，‎ 得：70x+80y≤530，‎ 不相同的选购方式有（3，2），（3，3），（3，4），（4，2），（4，3），（5，2），共6种方案．‎ 故选C．‎ 点评：‎ 解决本题的关键是根据总价钱得到相应的关系式，易错点是得到整数解的个数．‎ ‎　‎ ‎4．（2011•河北）如图，在矩形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长和宽分别为y和x，则y与x的函数图象大致是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 一次函数综合题；正比例函数的定义．2611678‎ 专题：‎ 数形结合．‎ 分析：‎ 从y﹣等于该圆的周长，即列方程式，再得到关于y的一次函数，从而得到函数图象的大体形状．‎ 解答：‎ 解：由题意 即，‎ 所以该函数的图象大约为A中函数的形式．‎ 故选A．‎ 点评：‎ 本题考查了一次函数的综合运用，从y﹣‎ 等于该圆的周长，从而得到关系式，即解得．‎ ‎　‎ 二．填空题（共2小题）‎ ‎5．二次函数y=ax2+bx+c若满足a﹣b+c=0，则其图象必经过点　（﹣1，0）　．‎ 考点：‎ 二次函数图象上点的坐标特征．2611678‎ 专题：‎ 计算题．‎ 分析：‎ 把x=﹣1代入y=ax2+bx+c得到y=a﹣b+c=0，即过（﹣1，0）点，即可得到答案．‎ 解答：‎ 解：把x=﹣1代入y=ax2+bx+c得：y=a﹣b+c=0，‎ ‎∴图象必过点：（﹣1，0），‎ 故答案为：（﹣1，0）．‎ 点评：‎ 本题主要考查对二次函数图象上点的坐标特征的理解和掌握，能根据已知a﹣b+c=0得出过（﹣1，0）是解此题的关键．‎ ‎　‎ ‎6．（2011•重庆）某步行街摆放有若干盆甲、乙、丙三种造型的盆景．甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成，乙种盆景由10朵红花和12朵黄花搭配而成，丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成．这些盆景一共用了2900朵红花，3750朵紫花，则黄花一共用了　4380　朵．‎ 考点：‎ 三元一次方程组的应用．2611678‎ 专题：‎ 应用题．‎ 分析：‎ 题中有两个等量关系：甲种盆景所用红花的朵数+乙种盆景所用红花的朵数+丙种盆景所用红花的朵数=2900朵，甲种盆景所用紫花的朵数+丙种盆景所用紫花的朵数=3750朵．据此可列出方程组，设步行街摆放有甲、乙、丙三种造型的盆景分别有x盆、y盆、z盆，用含x的代数式分别表示y、z，即可求出黄花一共用的朵数．‎ 解答：‎ 解：设步行街摆放有甲、乙、丙三种造型的盆景分别有x盆、y盆、z盆．‎ 由题意，有，‎ 由①得，3x+2y+2z=580③，‎ 由②得，x+z=150④，‎ 把④代入③，得x+2y=280，‎ ‎∴2y=280﹣x⑤，‎ 由④得z=150﹣x⑥．‎ ‎∴4x+2y+3z=4x+（280﹣x）+3（150﹣x）=730，‎ ‎∴黄花一共用了：24x+12y+18z=6（4x+2y+3z）=6×730=4380．‎ 故黄花一共用了4380朵．‎ 点评：‎ 本题考查了三元一次方程组在实际生活中的应用．解题的关键是发掘等量关系列出方程组，难点是将方程组中的其中一个未知数看作常数，用含有一个未知数的代数式表示另外两个未知数，然后代入所求黄花的代数式．‎ ‎　‎