2011年贵州省安顺市中考数学试卷及答案

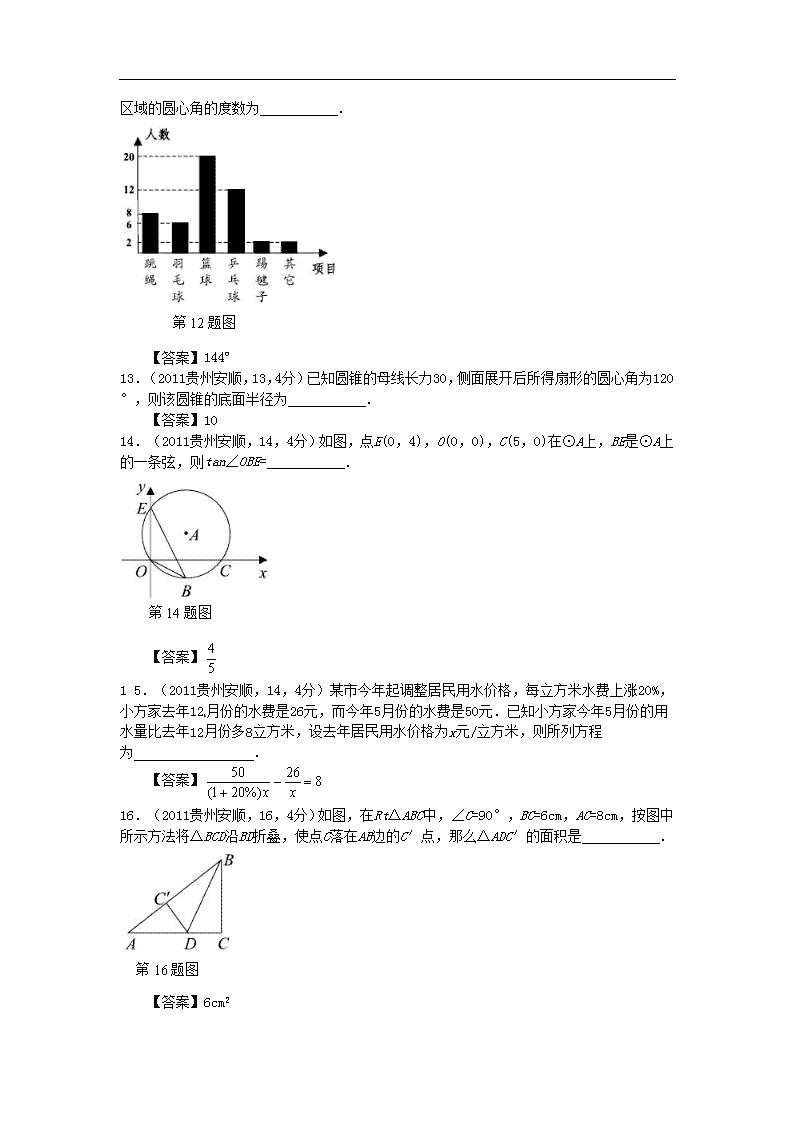
2011年贵州省安顺市中考数学试卷及答案

‎2011年贵州省安顺市初中毕业生学业招生考试 数 学 特别提示：‎ ‎ 1、本卷为数学科试题单，共27个题，满分150分．共4页．考试时间120分钟．‎ ‎ 2、考试采用闭卷形式，用笔在特制答题卡上答题，不能在本题单上作答．‎ ‎ 3、答题时请仔细阅读答题卡上的注意事项，并根据本题单各题的编号在答题卡上找到答题的对应位置，用规定的笔进行填涂和书写．‎ 一、单项选择题（共30分，每小题3分）‎ ‎1． （2011贵州安顺，1，3分）－4的倒数的相反数是（ ）‎ A．－4 B．‎4 ‎ C．－ D．‎ ‎【答案】D ‎2．（2011贵州安顺，2，3分）已知地球距离月球表面约为383900千米，那么这个距离用科学记数法表示为（保留三个有效数字）（ ）‎ A．3.84×104千米 B．3.84×105千米 C．3.84×106千米 D．38.4×104千米 ‎【答案】B ‎3．（2011贵州安顺，3，3分）如图，己知AB∥CD，BE平分∠ABC，∠CDE=150°，则∠C的度数是（ ）‎ A．100° B．110° C．120° D．150°‎ 第3题图 ‎【答案】C ‎4．（2011贵州安顺，4，3分）我市某一周的最高气温统计如下表：21世纪教育网 最高气温（℃）‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ 天 数 ‎1‎ ‎1‎ ‎2‎ ‎3‎ 则这组数据的中位数与众数分别是（ ）‎ A．27，28 B．27.5，‎28 ‎ C．28，27 D．26.5，27‎ ‎【答案】A ‎5．（2011贵州安顺，5，3分）若不等式组有实数解，则实数m的取值范围是（ ）‎ A．m≤ B．m＜ C．m＞ D．m≥‎ ‎【答案】A ‎6． （2011贵州安顺，6，3分）如图是几个小立方块所搭的几何体俯视图，小正方形中的数字表示该位置上小立方块的个数，则这个几何体的主视图是（ ）‎ A． B． C． D．‎ ‎【答案】A21世纪教育网 ‎7． （2011贵州安顺，7，3分）函数中自变量x的取值范围是（ ）‎ ‎ A．x≥0 B．x <0且x≠l C．x<0 D．x≥0且x≠l ‎【答案】D ‎8． （2011贵州安顺，8，3分）在Rt△ABC中，斜边AB =4，∠B= 60°，将△ABC绕点B按顺时针方向旋转60°，顶点C运动的路线长是（ ）‎ A． B． C．π D．‎ ‎【答案】B ‎9． （2011贵州安顺，9，3分）正方形ABCD边长为1，E、F、G、H分别为边AB、BC、CD、DA上的点，且AE=BF=CG=DH．设小正方形EFGH的面积为y，AE=x. 则y关于x的函数图象大致是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎10．（2011贵州安顺，10，3分）一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到(0，1)，然后接着按图中箭头所示方向跳动[即(0，0)→(0，1) →(1，1) →（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（ ）‎ ‎ A．(4，O) B.(5，0) C．(0，5) D．(5，5)‎ 第10题图 ‎【答案】B 二、填空题（共32分，每小题4分）‎ ‎11．（2011贵州安顺，11，4分）因式分解：x3－9x= ．‎ ‎【答案】x ( x-3 )( x+3 )‎ ‎12．（2011贵州安顺，12，4分）小程对本班50名同学进行了“我最喜爱的运动项目”的调查 ‎，统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数．根据调查结果绘制了人数分布直方图．若将其转化为扇形统计图，那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为 ．‎ 第12题图 ‎【答案】144º ‎ ‎13．（2011贵州安顺，13，4分）已知圆锥的母线长力30，侧面展开后所得扇形的圆心角为120°，则该圆锥的底面半径为 ．‎ ‎【答案】10‎ ‎14．（2011贵州安顺，14，4分）如图，点E(0，4)，O(0，0)，C(5，0)在⊙A上，BE是⊙A上的一条弦，则tan∠OBE= ．‎ 第14题图 ‎【答案】‎ ‎1 5．（2011贵州安顺，14，4分）某市今年起调整居民用水价格，每立方米水费上涨20%，小方家去年12月份的水费是26元，而今年5月份的水费是50元．已知小方家今年5月份的用水量比去年12月份多8立方米，设去年居民用水价格为x元/立方米，则所列方程为 ．‎ ‎【答案】‎ ‎16．（2011贵州安顺，16，4分）如图，在Rt△ABC中，∠C=90°，BC=‎6cm，AC=‎8cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是 ．‎ 第16题图 ‎【答案】‎6cm2‎ ‎17．（2011贵州安顺，17，4分）已知：如图，O为坐标原点，四边形OABC为矩形，A(10，0)，C(0，4)，点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为 ．‎ 第17题图 ‎【答案】P（3，4）或（2，4）或（8，4）‎ ‎18．（2011贵州安顺，18，4分）如图，在Rt△ABC中，∠C=90°，CA=CB=4，分别以A、B、C为圆心，以AC为半径画弧，三条弧与边AB所围成的阴影部分的面积是 ．‎ ‎ 第18题图 21世纪教育网 ‎【答案】‎ 三、解答题（本大题共9个小题，共88分）‎ ‎19．（2011贵州安顺，19，8分）计算：‎ ‎【答案】原式==2 ．‎ ‎20．（2011贵州安顺，20，8分）先化简，再求值：，其中a=2－‎ ‎【答案】原式=‎ ‎= ‎ ‎=‎ 当=时，原式=．‎ ‎21．（2011贵州安顺，21，8分）一次数学活动课上，老师带领学生去测一条南北流向的河宽，如图所示，某学生在河东岸点A处观测到河对岸水边有一点C，测得C在A北偏西31°的方向上，沿河岸向北前行‎40米到达B处，测得C在B北偏西45°的方向上，请你根据以上数据，求这条河的宽度．（参考数值：tan31°≈）‎ 第21题图 ‎【答案】过点C作CDAB于D ，‎ 第21题图 D 由题意，，设CD = BD = x米，则AD =AB+BD =（40+x）米，‎ 在Rt中，tan=，则，解得x = 60（米）．‎ ‎21世纪教育网 ‎22．（2011贵州安顺，22，10分）有A、B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B布袋中有三个完全相同的小球，分别标有数字－l，－2和－3．小强从A布袋中随机取出一个小球，记录其标有的数字为a，再从B布袋中随机取出一个小球，记录其标有的数字为b，这样就确定点Q的一个坐标为（a，b）．‎ ‎ ⑴用列表或画树状图的方法写出点Q的所有可能坐标；‎ ‎ ⑵求点Q落在直线y=x－3上的概率．‎ ‎【答案】（1）列表或画树状图略，点Q的坐标有 ‎（1，-1），（1，-2），（1，-3），（2，-1），（2，-2），（2，-3）；‎ ‎（2）“点Q落在直线y = x-3上”记为事件，所以，‎ 即点Q落在直线y = x-3上的概率为．‎ ‎23．（2011贵州安顺，23，10分）如图，已知反比例函数的图像经过第二象限内的点A（－1，m），AB⊥x轴于点B，△AOB的面积为2．若直线y=ax+b经过点A，并且经过反比例函数的图象上另一点C（n，一2）．‎ ‎ ⑴求直线y=ax+b的解析式；‎ ‎⑵设直线y=ax+b与x轴交于点M，求AM的长．‎ ‎ ‎第23题图 ‎【答案】（1）∵点A（-1，m）在第二象限内，∴AB = m，OB = 1，∴‎ 即：，解得，∴A (-1,4)，‎ ‎∵点A (-1,4)，在反比例函数的图像上，∴4 =，解得，‎ ‎∵反比例函数为，又∵反比例函数的图像经过C（n，）‎ ‎∴，解得，∴C (2,-2)，‎ ‎∵直线过点A (-1,4)，C (2,-2)‎ ‎∴ 解方程组得 ‎ ‎∴直线的解析式为 ；‎ ‎（2）当y = 0时，即解得，即点M（1，0）‎ 在中，∵AB = 4，BM = BO +OM = 1+1 = 2，‎ 由勾股定理得AM=．‎ ‎24．（2011贵州安顺，24，10分）某班到毕业时共结余班费1800元，班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品，其余资金用于在毕业晚会上给50位同学每人购买一件T恤或一本影集作为纪念品．已知每件T恤比每本影集贵9元，用200元恰好可以买到2件T恤和5本影集．‎ ‎⑴求每件T恤和每本影集的价格分别为多少元？‎ ‎⑵有几种购买T恤和影集的方案？‎ ‎【答案】（1）设T恤和影集的价格分别为元和元．则 ‎ ‎ 解得 答：T恤和影集的价格分别为35元和26元．‎ ‎（2）设购买T恤件，则购买影集 (50-) 本，则 解得，∵为正整数，∴= 23，24，25，‎ 即有三种方案．第一种方案：购T恤23件，影集27本；‎ 第二种方案：购T恤24件，影集26本；‎ 第三种方案：购T恤25件，影集25本．‎ ‎25．（2011贵州安顺，25，10分）如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，且AF=CE=AE．‎ ‎⑴说明四边形ACEF是平行四边形；‎ ‎⑵当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．‎ 第25题图 ‎【答案】（1）证明：由题意知∠FDC =∠DCA = 90°．∴EF∥CA ∴∠AEF =∠EAC ‎∵AF = CE = AE ∴∠F =∠AEF =∠EAC =∠ECA 又∵AE = EA ‎∴△AEC≌△EAF，∴EF = CA，∴四边形ACEF是平行四边形 ．‎ ‎（2）当∠B=30°时，四边形ACEF是菱形 ．‎ 理由是：∵∠B=30°，∠ACB=90°，∴AC=，∵DE垂直平分BC，∴ BE=CE 又∵AE=CE，∴CE=，∴AC=CE，∴四边形ACEF是菱形．‎ ‎26．（2011贵州安顺，26，12分）已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．‎ ‎⑴求证：点D是AB的中点；‎ ‎⑵判断DE与⊙O的位置关系，并证明你的结论；‎ ‎⑶若⊙O的直径为18，cosB =，求DE的长．‎ 第26题图 ‎【答案】（1）证明：连接CD,则CD， 又∵AC = BC， CD = CD， ∴≌‎ ‎∴AD = BD ， 即点D是AB的中点．‎ 第26题图 ‎（2）DE是⊙O的切线 ． ‎ 理由是：连接OD, 则DO是△ABC的中位线，∴DO∥AC ， 又∵DE；‎ ‎∴DE 即DE是⊙O的切线；‎ ‎（3）∵AC = BC， ∴∠B =∠A ， ∴cos∠B = cos∠A =， ∵ cos∠B =， BC = 18，‎ ‎∴BD = 6 ， ∴AD = 6 ， ∵ cos∠A = ， ∴AE = 2，‎ 在中，DE=．‎ ‎27．（2011贵州安顺，27，12分）如图，抛物线y=x2+bx－2与x轴交于A、B两点，与y轴交于C点，且A（一1，0）．‎ ‎⑴求抛物线的解析式及顶点D的坐标；‎ ‎⑵判断△ABC的形状，证明你的结论；‎ ‎⑶点M(m，0)是x轴上的一个动点，当CM+DM的值最小时，求m的值．‎ 第27题图 ‎【答案】（1）∵点A（-1，0）在抛物线y=x2 + bx-2上，∴× (-1 )2 + b× (-1) –2 = 0，解得b =‎ ‎∴抛物线的解析式为y=x2-x-2. y=x2-x-2 = ( x2 -3x- 4 ) =(x-)2-,‎ ‎∴顶点D的坐标为 (, -). ‎ ‎（2）当x = 0时y = -2, ∴C（0，-2），OC = 2。‎ 当y = 0时， x2-x-2 = 0， ∴x1 = -1, x2 = 4, ∴B (4,0)‎ ‎∴OA = 1, OB = 4, AB = 5.‎ ‎∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,‎ ‎∴AC2 +BC2 = AB2. ∴△ABC是直角三角形.‎ ‎（3）作出点C关于x轴的对称点C′，则C′（0，2），OC′=2，连接C′D交x轴于点M，根据轴对称性及两点之间线段最短可知，MC + MD的值最小。‎ 解法一：设抛物线的对称轴交x轴于点E.‎ ‎∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM ‎∴△C′OM∽△DEM. ‎ ‎∴‎ ‎∴，∴m =．‎ 解法二：设直线C′D的解析式为y = kx + n ,‎ 则，解得n = 2, .‎ ‎∴ .2‎ ‎∴当y = 0时， ，‎ ‎ . ∴.‎