中考数学专题复习九 图形的变换与四边形练习

中考数学专题复习九 图形的变换与四边形练习

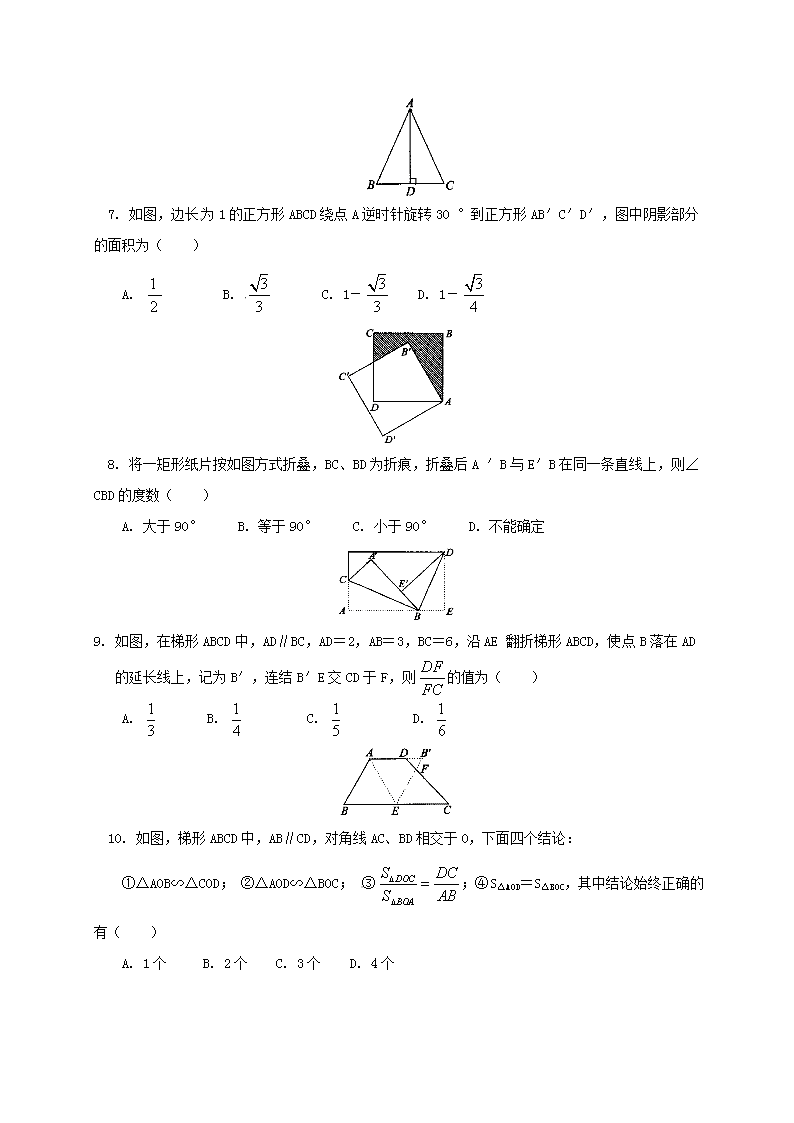
专题九 图形的变换与四边形 一、选择题 ‎1. 将叶片图案旋转180°后，得到的图形是（ ）‎ ‎2. 下列图形中，不是轴对称图形的是（ ）‎ ‎3. 下图是用12个全等的等腰梯形镶嵌成的图形，这个图形中等腰梯形的上底长与下底长的比是（ ）‎ ‎ A. 1：2 B. 2：‎1 C. 3：1 D. 1：3‎ ‎4. 张明同学设计了四种正多边形的瓷砖图案，在这四种瓷砖图案中，不能铺满地面的是（ ）‎ ‎5. 如图，一块含有30°角的直角三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置．若BC的长为‎15cm，那么顶点A从开始到结束所经过的路径长为（ ）‎ ‎ A. 10cm B. 10cm C. 15cm D. 20cm ‎ ‎6. 如图，AB＝AC，AD⊥BC，AD＝BC，若用剪刀沿AD剪开，则最多能拼出不同形状的四边形的个数是（ ）‎ A. 2个 B. 3个 C. 4个 D. 5个 ‎ ‎7. 如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，图中阴影部分的面积为（ ）‎ A. B. C. 1－ D. 1－‎ ‎8. 将一矩形纸片按如图方式折叠，BC、BD为折痕，折叠后A′B与E′B在同一条直线上，则∠CBD的度数（ ）‎ ‎ A. 大于90° B. 等于90° C. 小于90° D. 不能确定 ‎9. 如图，在梯形ABCD中，AD∥BC，AD＝2，AB＝3，BC＝6，沿AE翻折梯形ABCD，使点B落在AD的延长线上，记为B′，连结B′E交CD于F，则的值为（ ）‎ ‎ A. B. C. D. ‎ ‎10. 如图，梯形ABCD中，AB∥CD，对角线AC、BD相交于O，下面四个结论：‎ ‎ ①△AOB∽△COD； ②△AOD∽△BOC； ③；④S△AOD＝S△BOC，其中结论始终正确的有（ ）‎ A. 1个 B. 2个 C. 3个 D. 4个 二、填空题 ‎1. 如图，四边形ABCD中，AB∥CD，要使四边形ABCD为平行四边形，则应添加的条件是_____________（添加一个条件即可）．‎ ‎2. 如图，将边长为‎8cm的正方形ABCD的四边沿直线l向右滚动（不滑动），当正方形滚动两周时，正方形的顶点A所经过的路线的长是________cm．‎ ‎3. 用两个全等的直角三角形拼下列图形：①平行四边形；②矩形；③菱形；④正方形；⑤等腰三角形；⑥等边三角形；一定可以拼成的是________（只填序号）．‎ ‎4. 如图，先将一矩形ABCD置于直角坐标系中，使点A与坐标系的原点重合，边AB、AD分别落在x轴、y轴上（如图①所示），再将此矩形在坐标平面内按逆时针方向绕原点旋转30°（如图②所示），若AB＝4，BC＝3，则图①和图②中，点B的坐标为 ‎ ‎________，点C的坐标为______．‎ ‎5. 如图，在梯形ABCD中，∠DCB＝90°，AB∥CD，AB＝25，BC＝24. 将该梯形折叠，点A恰好与点D重合，BE为折痕，那么AD的长度为_______．‎ 三、解答题 ‎1. 在下图的方格纸中有一个Rt△ABC（A、B、C三点均为格点），∠C＝90°．‎ ‎ （1）请你画出将Rt△ABC绕点C顺时针旋转90°后所得到的Rt△A′B′C. 其中A、B的对应点分别是A′，B′（不必写画法）；‎ ‎ （2）设（1）中AB的延长线与A′B′相交于D点，方格纸中每一个小正方形的边长为1，试求BD的长（精确到0.1）．‎ ‎2. 在AB＝‎30m，AD＝‎20m的矩形ABCD的花坛四周修筑小路．‎ ‎ （1）如果四周的小路的宽均相等，如图（1），那么小路四周所围成的矩形A′B′C′D′和矩形ABCD相似吗？请说明理由．‎ ‎（2）如果相对着的两条小路的宽均相等，如图（2），试问小路的宽x与y的比值为多少时，能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似？请说明理由．‎ ‎3. 如图，在梯形ABCD中，AD∥BC，AB＝DC＝AD，∠ADC＝120°．‎ 求证：（1）BD⊥DC；（2）若AB＝4，求梯形ABCD的面积．‎ ‎4. 如图，在梯形ABCD中，AD∥BC，AB＝DC，∠B＝60°，DE∥AB. ‎ ‎ 求证：（1）DE＝DC；（2）△DEC是等边三角形．‎ ‎5. 如图，在△ABC中，∠ACB＝90°，AC＝2，BC＝3. D是BC边上一点，直线DE⊥BC于D，交AB于E，CF∥AB交直线DF于F．设CD＝x．‎ ‎ （1）当x取何值时，四边形EACF是菱形？请说明理由；‎ ‎ （2）当x取何值时，四边形EACD的面积等于2？‎ 练习答案 一、选择题 ‎1. D 2. A 3. A 4. C 5. D 6. D 7. C 8. B 9. A 10. B ‎ 二、填空题 ‎1. 答案不唯一，如AB＝CD等 ‎2. 16＋16‎ ‎3. ①②⑤‎ ‎4. B（4，0），（2，2），C（4，3），（）‎ ‎5. 30.‎ 三、解答题 ‎1. 解：（1）方格纸中Rt△A′B′C为所画的三角形 ‎ ‎（2）由（1）得∠A＝∠A′，‎ 又∵∠1＝∠2，∴△ABC∽△A′BD，‎ ‎∴，‎ ‎∵BC＝1，A′B＝2，‎ AB＝，‎ 即BD＝≈0.6，∴BD的长约为0.6‎ ‎ 2. 解：①当x≠0时，‎ 故矩形A′B′C′D′和矩形ABCD不相似 ‎ ‎②当时，矩形A′B′C′D′和矩形ABCD相似 所以，解得＝‎ ‎3. 证明：（1）由∠ADC＝120°，可得∠C＝∠ABC＝60°，‎ 从而得到∠ADB＝30°，∴BD⊥DC. ‎ ‎（2）12 ‎ ‎4. 证明：（1）∵AD∥BC，DE∥AB，‎ ‎∴四边形ABED是平行四边形，‎ ‎∴DE＝AB，‎ ‎∵AB＝DC，‎ ‎∴DE＝DC ‎ ‎（2）∵AD∥BC，AB＝DC，∠B＝60°，‎ ‎∴∠C＝∠B＝60°．‎ 又∵DE＝DC，‎ ‎∴△DEC是等边三角形．‎ ‎5. 解：（1）∵∠ACB＝90°，‎ ‎∴AC⊥BC. 又∵DE⊥BC，∴EF∥AC．‎ 又∵AE∥CF，∴四边形EACF是平行四边形．‎ 当CF＝AC时，四边形ACFE是菱形．‎ 此时，CF＝AC＝2，BD＝3－x，tan∠B＝，ED＝BD·tan∠B＝（3－x），‎ ‎∴DF＝EF－ED＝2－（3－x）＝x．‎ 在Rt△CDF中，CD2＋DF2＝CF2，‎ ‎∴x2＋（x）2＝22，∴x＝±（负值不合题意，舍去），‎ 即当x＝时，四边形ACFE是菱形 ‎ ‎（2）由已知得，四边形EACD是直角梯形，S梯形EACD＝×（4－x）·x＝－x2＋2x．‎ 依题意，得－x2＋2x＝2，整理得，x2－6x＋6＝0. 解之，得x1＝3－，x2＝3＋．‎ ‎∵x＝3＋>BC＝3，‎ ‎∴x＝3＋舍去，‎ ‎∴当x＝3－时，梯形EACD的面积等于2．‎