- 2021-05-10 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2010年四川省内江市中考数学试卷及答案
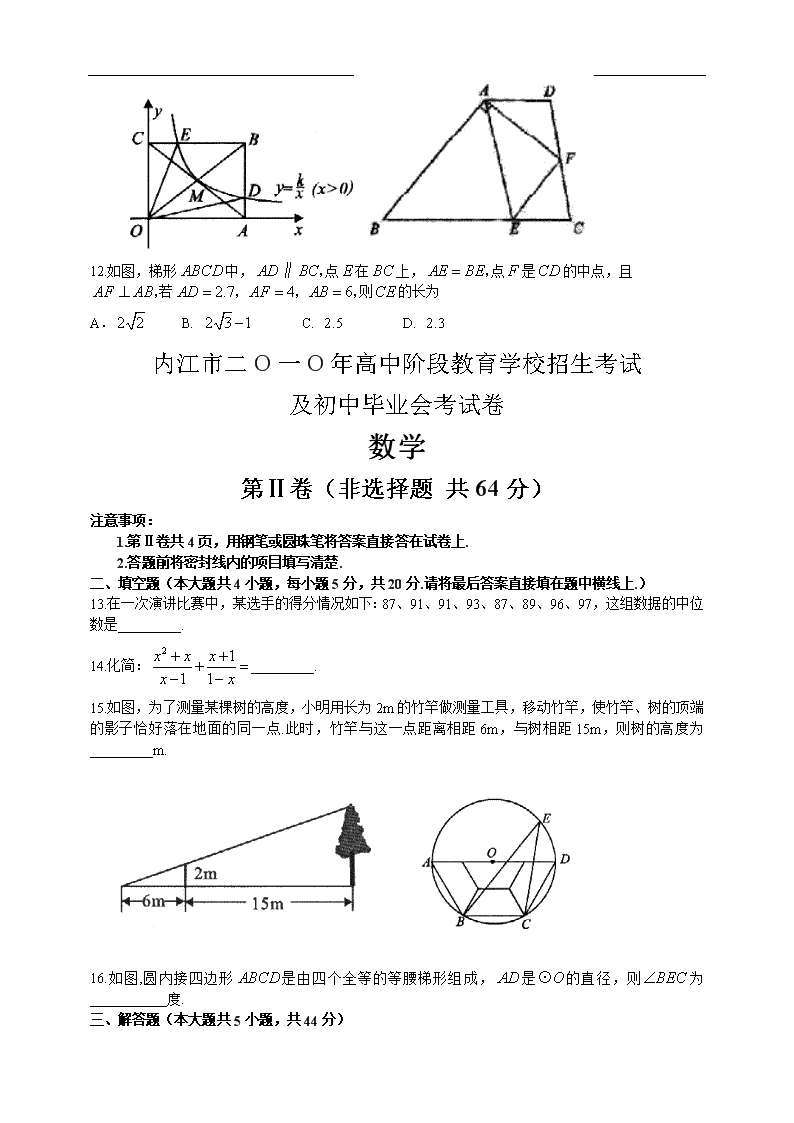
内江市二O一O年高中阶段教育学校招生考试 及初中毕业会考数学试卷 本试卷分会考卷和加试卷两部分,会考卷1至6页,满分100分;加试卷7至10页,满分60分.全卷满分160分,120分钟完卷. 注意事项: 1.答题前,考生务必将密封线内的内容填写清楚,将自己的姓名、准考证号、考试科目等涂写在机读卡上. 2.答第Ⅰ卷时,每小题选出答案后,用铅笔把机读卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后再选涂其它答案. 3.只参加毕业会考的考生只需做会考卷,要参加加升学考试的考生须完成会考卷和加试卷两部分. 4.考试结束后,将本试卷和机读卡一并收回. 第Ⅰ卷(选择题 共36分) 一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.的倒数是 A. B. C. D. 2.截止2010年4月20日23时35分,央视“情系玉树,大爱无疆”赈灾晚会共收到社会各界为玉树捐款2 175 000 000元,用科学记数法表示捐款数应为 A.元 B. 元 C. 元 D. 元 3.下列图形是正方体的表面展开图的是 A B C D 4.下列事件中为必然事件的是 A.早晨的太阳一定从东方升起 B.打开数学课本时刚好翻到第60页 C从一定高度落下的图钉,落地后钉尖朝上. D.今年14岁的小云一定是初中学生 5.将一副三角板如图放置,使点在上,则的度数为 A. B. C. D. 6.函数中,自变量的取值范围是 A. B. C. 且 D. 且 7.方程的解是 A. B. C. D. 8.某品牌服装折扣店将某件衣服按进价提高50%后标价,再打8折(标价的80%)销售,售价为240元.设这件衣服的进价为元,根据题意,下面所列的方程正确的是 A. B. C. D. 9.学剪五角星:如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚剪下展开即可得到一个五角星.如果想得到一个正五角星(如图④),那么在图③中剪下时,应使的度数为 ① ② ③ ④ A. B. C. D. 10.在四张完全相同的卡片上分别印有等边三角形、平行四边形、等腰梯形、圆的图案,现将印有图案的一面朝下,混合后从中一次性随机抽取两张,则抽到的卡片上印有的图案都是轴对称图形的概率为 A. B. C. D. 11.如图,反比例函数的图象经过矩形对角线的交点分别与相交于点若四边形的面积为6,则的值为 A.1 B. 2 C. 3 D. 4 12.如图,梯形中,点在上,点是的中点,且 若则的长为 A. B. C. D. 内江市二O一O年高中阶段教育学校招生考试 及初中毕业会考试卷 数学 第Ⅱ卷(非选择题 共64分) 注意事项: 1.第Ⅱ卷共4页,用钢笔或圆珠笔将答案直接答在试卷上. 2.答题前将密封线内的项目填写清楚. 二、填空题(本大题共4小题,每小题5分,共20分.请将最后答案直接填在题中横线上.) 13.在一次演讲比赛中,某选手的得分情况如下:87、91、91、93、87、89、96、97,这组数据的中位数是_________. 14.化简:_________. 15.如图,为了测量某棵树的高度,小明用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度为_________m. 16.如图,圆内接四边形是由四个全等的等腰梯形组成,是的直径,则为___________度. 三、解答题(本大题共5小题,共44分) 17.(7分) 已知 (1)请化简这四个数; (2)根据化简结果,列式表示这四个数中“有理数的和”与“无理数的积”的差,然后计算结果. 18.(9分) 如图,和都是等腰直角三角形,交于点分别交于点 试猜测线段和的数量和位置关系,并说明理由. 19.(9分) 学校为了解学生参加体育活动的情况,对学生“平均每天参加体育活动的时间”进行了随机抽样调查,下图是根据调查结果绘制的两幅不完整的统计图. 请你根据统计图提供的信息,解答以下问题: (1)“平均每天参加体育活动的时间”“为0.5~1小时”部分的扇形统计图的圆心角为______度; (2)本次一共调查了_________名学生; (3)将条形统计图补充完整; (4)若该校有2000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下. 20.(9分) 为建设“宜居宜业宜游”山水园林式城市,内江市正在对城区沱江河段进行区域性景观打造. 如图,某施工单位为测得某河段的宽度,测量员先在河对岸边取一点再在河这边沿河边取 两点在点处测得点在北偏东方向上,在点处测得点在西北方向上,量 得长为200米.请你求出该河段的宽度(结果保留根号). 21. (10分) 一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示: 销售方式 粗加工后销售 精加工后销售 每吨获利(元) 1000 2000 已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完. (1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工? (2)如果先进行精加工,然后进行粗加工. ①试求出销售利润元与精加工的蔬菜吨数之间的函数关系式; ②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间? 内江市二O一O年高中阶段教育学校招生考试 及初中毕业会考试卷 数学 加试卷(共60分) 题号 一 二 总分 总分人 5 6 7 得分 注意事项: 加试卷共4页,请将答案直接写在试卷上. 一、选择题(本大题共4小题,每小题6分,共24分.请将最简答案直接填写在题中横线上.) 1.已知则___________. 2.下面的方格图案中的正方形顶点叫做格点,图1中以格点为顶点的等腰直角三角形共有4个,图2中以格点为顶点的等腰直角三角形共有___________个,图3中以格点为顶点的等腰直角三角形共有___________个,图4中以格点为顶点的等腰直角三角形共有___________个. 3.已知非负数满足条件设的最大值为最小值为则的值为___________. 4.如图,在中,点分别在和上,与相交于点若为的中点,的值为___________. 二、解答题(本大题共3个小题,每小题12分,共36分.解答题必须写出必要的文字说明、证明过程或推演步骤.) 5.(12分) 阅读理解: 我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点 的对称中心的坐标为 观察应用: (1)如图,在平面直角坐标系中,若点的对称中心是点则点的坐 标为_________; (2)另取两点有一电子青蛙从点处开始依次关于点 作循环对称跳动,即第一次跳到点关于点的对称点处,接着跳到点关于点的对 称点处,第三次再跳到点关于点的对称点处,第四次再跳到点关于点的对称点 处,…则点的坐标分别为_________、_________. 拓展延伸: (3)求出点的坐标,并直接写出在轴上与点、点构成等腰三角形的点的坐标. 6.(12分) 如图,在中,点在斜边上,以为直径的与相切于 点 (1)求证:平分 (2)若 ①求的值;②求图中阴影部分的面积. 7.(12分) 如图,抛物线与轴交于两点,与轴交于点. (1)请求出抛物线顶点的坐标(用含的代数式表示),两点的坐标; (2)经探究可知,与的面积比不变,试求出这个比值; (3)是否存在使为直角三角形的抛物线?若存在,请求出;如果不存在,请说明 理由. 参考答案及评分意见 会考卷(共100分) 一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.A 2.B 3.C 4.A 5.D 6.C 7.D 8.B 9.A 10.C 11.B 12.D 二、填空题(本大题共4小题,每小题5分,共20分.请将最后答案直接填在题中横线上.) 13.91 14. 15.7 16.30 三、解答题(本大题共5小题,共44分) 17.解:(1), 4分 (2)为有理数,为无理数, 5分 6分 = 7分 18.解:猜测 2分 理由如下: 即 3分 和都是等腰直角三角形. 4分 5分 6分 7分 8分 9分 19.解:(1)54 2分 (2)200 4分 7分 (3)(人) 9分 20.解:过点作于点. 1分 据题意, 2分 4分 在中, 7分 9分 答:该河段的宽度为()米. 21.解:(1)设应安排天进行精加工,天进行粗加工, 1分 根据题意得 3分 解得 答:应安排4天进行精加工,8天进行粗加工. 4分 (2)①精加工吨,则粗加工()吨,根据题意得 = 6分 ②要求在不超过10天的时间内将所有蔬菜加工完, 解得 8分 又在一次函数中,, 随的增大而增大, 当时, 9分 精加工天数为=1, 粗加工天数为 安排1天进行精加工,9天进行粗加工,可以获得最多利润为元. 10分 加试卷(共60分) 一、填空题(本大题共4小题,每小题6分,共24分.请将最简答案直接填在题中横线上.) 1.28 2.10,28,50 3.7 4. 二、解答题(本大题共3个小题,每小题12分,共36分.解答题必须写出必要的文字说明、证明过程或推演步骤.) 5.解:(1)(1,1) 2分 (2)() 4分 (2,3) 6分 (3)→→→→→→→… 的坐标和的坐标相同,的坐标和的坐标相同,即坐标以6为周期循环. 335…2, 的坐标与的坐标相同,为; 8分 在轴上与点、点构成等腰三角形的点的坐标为 12分 6.(1)证明:连接,则,. 1分 是的切线, 2分 平分 4分 (2)①连结,为直径, 又由(1)知 6分 7分 , 8分 ②在中, 9分 10分 11分 12分 7.解:(1) 抛物线顶点的坐标为(1,m) 2分 抛物线与轴交于两点, 当时, 解得 两点的坐标为()、(). 4分 (2)当时,, 点的坐标为. 5分 过点作轴于点,则 = = =3m. 7分 8分 (3)存在使为直角三角形的抛物线. 过点作于点,则为, 在中, 在中, ①如果是,且那么 即 解得, 存在抛物线使得是; 10分 ②如果是,且那么 即 解得, 存在抛物线,使得是; ③如果是,且,那么 即 整理得此方程无解. 以为直角的直角三角形不存在. 综上所述,存在抛物线和 使得是. 12分查看更多