- 2021-05-10 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北京市朝阳区中考数学二模试卷0
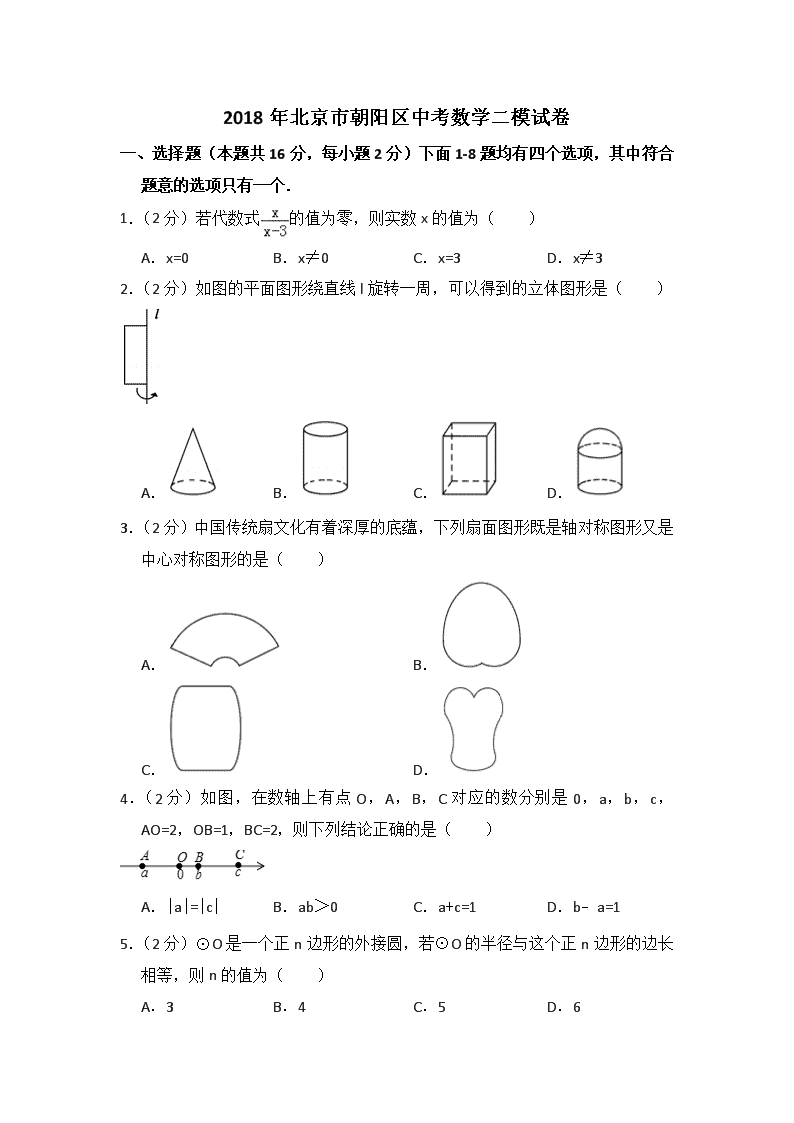
2018年北京市朝阳区中考数学二模试卷 一、选择题(本题共16分,每小题2分)下面1-8题均有四个选项,其中符合题意的选项只有一个. 1.(2分)若代数式的值为零,则实数x的值为( ) A.x=0 B.x≠0 C.x=3 D.x≠3 2.(2分)如图的平面图形绕直线l旋转一周,可以得到的立体图形是( ) A. B. C. D. 3.(2分)中国传统扇文化有着深厚的底蕴,下列扇面图形既是轴对称图形又是中心对称图形的是( ) A. B. C. D. 4.(2分)如图,在数轴上有点O,A,B,C对应的数分别是0,a,b,c,AO=2,OB=1,BC=2,则下列结论正确的是( ) A.|a|=|c| B.ab>0 C.a+c=1 D.b﹣a=1 5.(2分)⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,则n的值为( ) A.3 B.4 C.5 D.6 6.(2分)已知a2﹣5=2a,代数式(a﹣2)2+2(a+1)的值为( ) A.﹣11 B.﹣1 C.1 D.11 7.(2分)小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法: ①这栋居民楼共有居民140人 ②每周使用手机支付次数为28~35次的人数最多 ③有的人每周使用手机支付的次数在35~42次 ④每周使用手机支付不超过21次的有15人 其中正确的是( ) A.①② B.②③ C.③④ D.④ 8.(2分)如图,矩形ABCD中,AB=4,BC=3,F是AB中点,以点A为圆心,AD为半径作弧交AB于点E,以点B为圆心,BF为半径作弧交BC于点G,则图中阴影部分面积的差S1﹣S2为( ) A. B. C. D.6 二、填空题(本题共16分,每小题2分) 9.(2分)写出一个比大且比小的有理数: . 10.(2分)直线AB,BC,CA的位置关系如图所示,则下列语句:①点A在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④ 点B是直线AB,BC,CA的公共点,正确的有 (只填写序号). 11.(2分)2017年5月5日我国自主研发的大型飞机C919成功首飞,如图给出了一种机翼的示意图,用含有m、n的式子表示AB的长为 . 12.(2分)如图,△ABC内接于⊙O,AB是⊙O的直径,点D在圆O上,BD=CD,AB=10,AC=6,连接OD交BC于点E,DE= . 13.(2分)鼓励科技创新、技术发明,北京市2012﹣2017年专利授权量如图所示.根据统计图中提供信息,预估2018年北京市专利授权量约 件,你的预估理由是 . 14.(2分)如图,在平面直角坐标系xOy中,四边形OABC是正方形,点C(0,4),D是OA中点,将△CDO以C为旋转中心逆时针旋转90°后,再将得到的三角形平移,使点C与点O重合,写出此时点D的对应点的坐标: . 15.(2分)下列对于随机事件的概率的描述: ①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”; ②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2; ③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85 其中合理的有 (只填写序号). 16.(2分)下面是“作三角形一边上的高”的尺规作图过程. 已知:△ABC. 求作:△ABC的边BC上的高AD. 作法:如图2, (1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点E; (2)作直线AE交BC边于点D.所以线段AD就是所求作的高. 请回答:该尺规作图的依据是 . 三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26-27题,每小题5分,第28题8分) 17.(5分)计算:﹣3tan30°+(2018﹣π)0﹣()﹣1. 18.(5分)解不等式﹣3>2x﹣1,并把解集在数轴上表示出来. 19.(5分)如图,△ABC中,∠C=90°,AC=BC,∠ABC的平分线BD交AC于点D,DE⊥AB于点E. (1)依题意补全图形; (2)猜想AE与CD的数量关系,并证明. 20.(5分)已知关于x的一元二次方程x2+2(m﹣1)x+m2﹣3=0有两个不相等的实数根. (1)求m的取值范围; (2)若m为非负整数,且该方程的根都是无理数,求m的值. 21.(5分)如图,在平面直角坐标系xOy中,直线y=k1x+6与函数y=(x>0)的图象的两个交点分别为A(1,5),B. (1)求k1,k2的值; (2)过点P(n,0)作x轴的垂线,与直线y=k1x+6和函数y=(x>0)的图象的交点分别为点M,N,当点M在点N下方时,写出n的取值范围. 22.(5分)如图,平行四边形ABCD的对角线AC,BD相交于点O,延长CD到E,使DE=CD,连接AE. (1)求证:四边形ABDE是平行四边形; (2)连接OE,若∠ABC=60°,且AD=DE=4,求OE的长. 23.(5分)AB为⊙O直径,C为⊙O上的一点,过点C的切线与AB的延长线相交于点D,CA=CD. (1)连接BC,求证:BC=OB; (2)E是中点,连接CE,BE,若BE=2,求CE的长. 24.(5分)“绿水青山就是金山银山”,北京市民积极参与义务植树活动.小武同学为了了解自己小区300户家庭在2018年4月份义务植树的数量,进行了抽样调查,随即抽取了其中30户家庭,收集的数据如下(单位:棵): 1 1 2 3 2 3 2 3 3 4 3 3 4 3 3 5 3 4 3 4 4 5 4 5 3 4 3 4 5 6 (1)对以上数据进行整理、描述和分析: ①绘制如下的统计图,请补充完整; ②这30户家庭2018年4月份义务植树数量的平均数是 ,众数是 ; (2)“互联网+全民义务植树”是新时代首都全民义务植树组织形式和尽责方式的一大创新,2018年首次推出义务植树网上预约服务,小武同学所调查的这30户家庭中有7户家庭采用了网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有 户. 25.(6分)在数学活动课上,老师提出了一个问题:把一副三角尺如图1摆放,直角三角尺的两条直角边分别垂直或平行, 60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗? 小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究. 下面是小林的探究过程,请补充完整: (1)画出几何图形,明确条件和探究对象; 如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm. (2)通过取点、画图、测量,得到了x与y的几组值,如下表: x/cm 0 1 2 3 4 5 6 y/cm 6.9 5.3 4.0 3.3 4.5 6 (说明:补全表格时相关数据保留一位小数) (3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象; (4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为cm. 26.(7分)已知二次函数y=ax2﹣2ax﹣2(a≠0). (1)该二次函数图象的对称轴是直线; (2)若该二次函数的图象开口向上,当﹣1≤x≤5时,函数图象的最高点为M,最低点为N,点M的纵坐标为,求点M和点N的坐标; (3)对于该二次函数图象上的两点A(x1,y1),B(x2,y2),设t≤x1≤t+1,当x2≥3时,均有y1≥y2,请结合图象,直接写出t的取值范围. 27.(7分)如图,在△ABC中,AB=AC,∠BAC=90°,M是BC的中点,延长AM到点D,AE=AD,∠EAD=90°,CE交AB于点F,CD=DF. (1)∠CAD= 度; (2)求∠CDF的度数; (3)用等式表示线段CD和CE之间的数量关系,并证明. 28.(8分)对于平面直角坐标系xOy中的点P和直线m,给出如下定义:若存在一点P,使得点P到直线m的距离等于1,则称P为直线m的平行点. (1)当直线m的表达式为y=x时, ①在点P1(1,1),P2(0,),P3(,)中,直线m的平行点是 ; ②⊙O的半径为,点Q在⊙O上,若点Q为直线m的平行点,求点Q的坐标. (2)点A的坐标为(n,0),⊙A半径等于1,若⊙A上存在直线的平行点,直接写出n的取值范围. 2018年北京市朝阳区中考数学二模试卷 参考答案 一、选择题(本题共16分,每小题2分)下面1-8题均有四个选项,其中符合题意的选项只有一个. 1.A; 2.B; 3.C; 4.C; 5.D; 6.D; 7.B; 8.A; 二、填空题(本题共16分,每小题2分) 9.答案不唯一,如:2; 10.③; 11.m+n﹣n; 12.2; 13.113407;北京市近两年的专利授权量平均每年增加6458.5件; 14.(4,2); 15.②③; 16.到一条线段两个端点距离相等的点,在这条线段的垂直平分线上;三角形的高的定义;两点确定一条直线; 三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26-27题,每小题5分,第28题8分) 17. ; 18. ; 19. ; 20. ; 21. ; 22. ; 23. ; 24.3.4棵;3棵;70; 25.3.5; 26. ; 27.45; 28.P2,P3; 声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布 日期:2018/12/22 14:33:58;用户:qgjyuser10307;邮箱:qgjyuser10307.21957750;学号:21985313查看更多