中考数学专题训练定值和最值问题解析版

中考数学专题训练定值和最值问题解析版

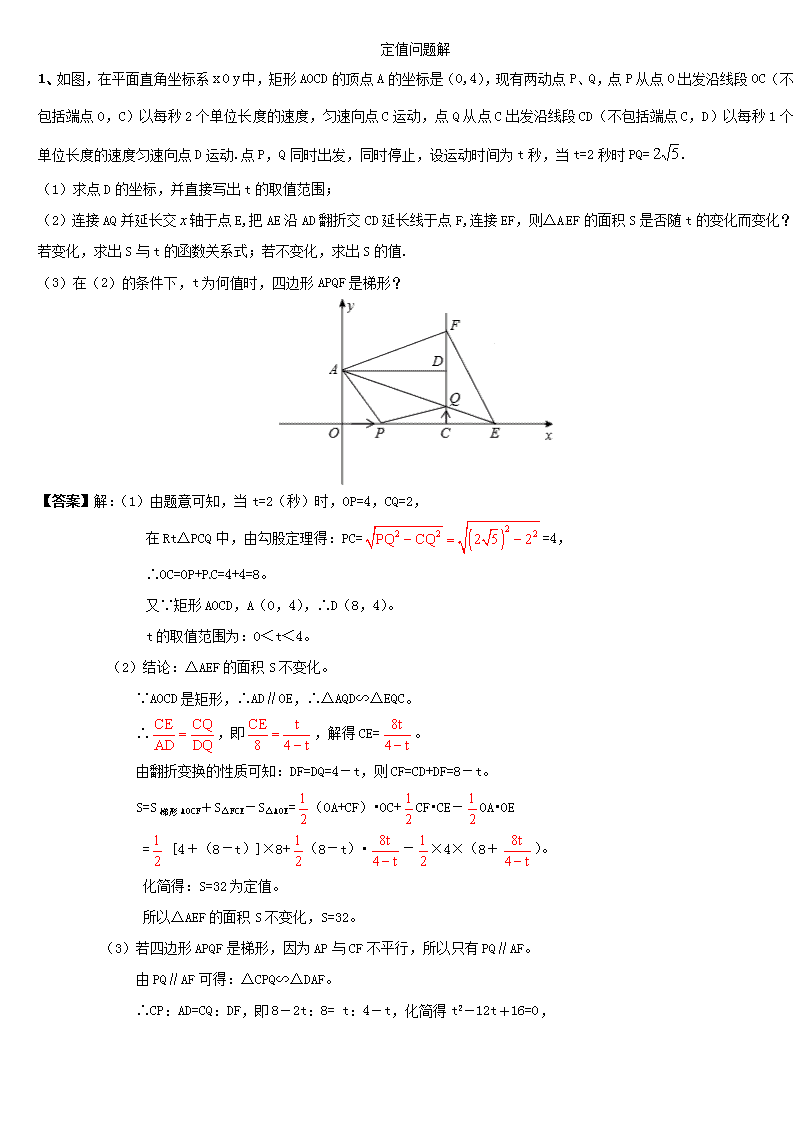
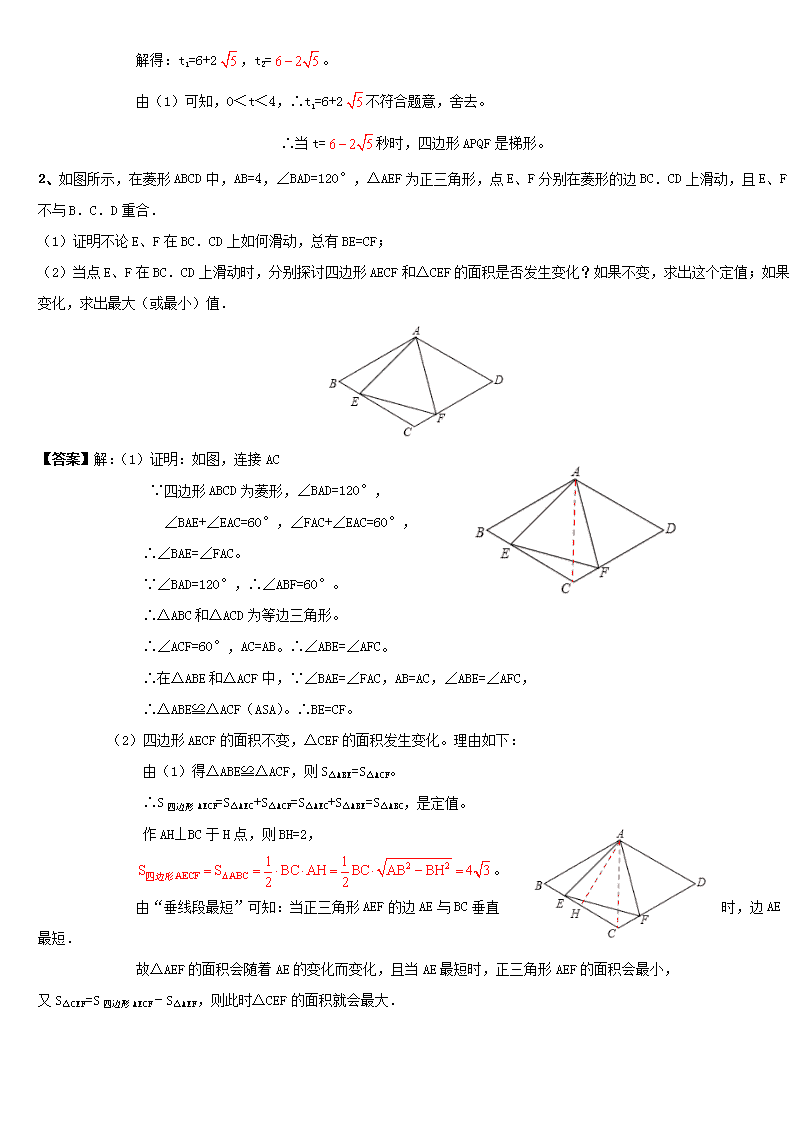
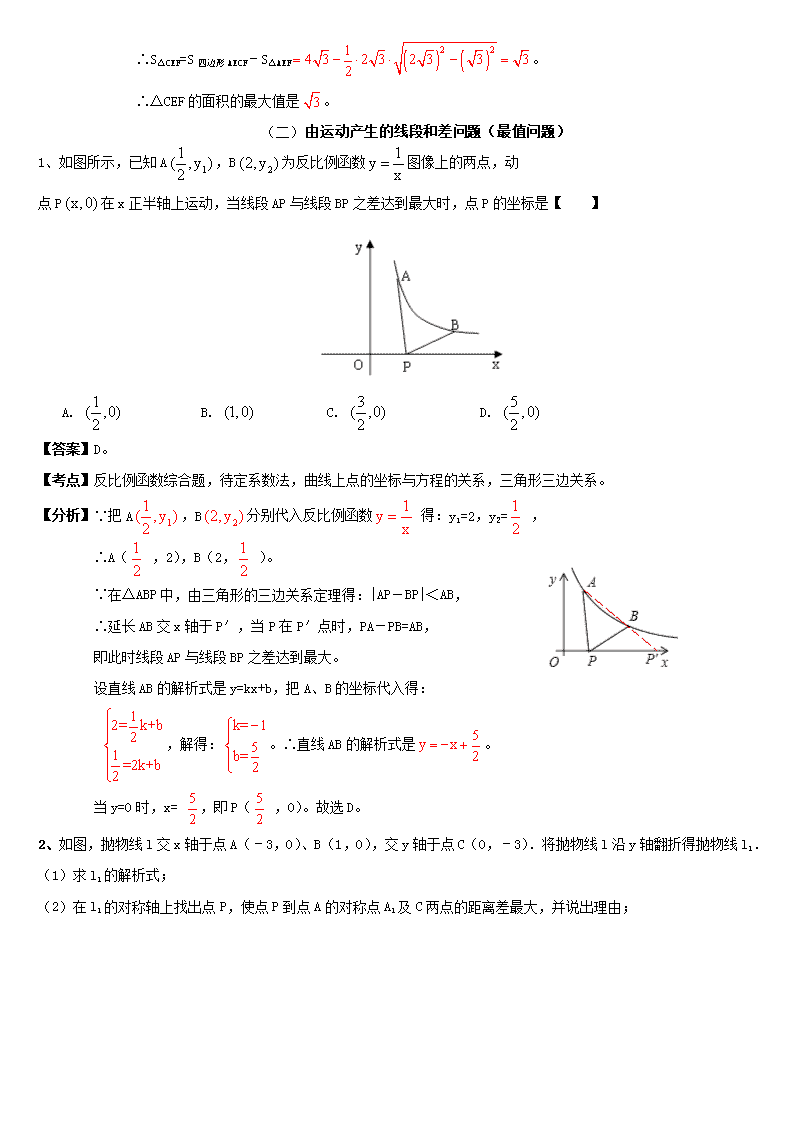
定值问题解 ‎1、如图，在平面直角坐标系O中，矩形AOCD的顶点A的坐标是（0,4），现有两动点P、Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度，匀速向点C运动，点Q从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动.点P，Q同时出发，同时停止，设运动时间为t秒，当t=2秒时PQ=.‎ ‎（1）求点D的坐标，并直接写出t的取值范围；‎ ‎（2）连接AQ并延长交轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF，则△AEF的面积S是否随t的变化而变化？若变化，求出S与t的函数关系式；若不变化，求出S的值.‎ ‎（3）在（2）的条件下，t为何值时，四边形APQF是梯形？‎ ‎【答案】解：（1）由题意可知，当t=2（秒）时，OP=4，CQ=2，‎ 在Rt△PCQ中，由勾股定理得：PC==4，‎ ‎∴OC=OP+PC=4+4=8。‎ 又∵矩形AOCD，A（0，4），∴D（8，4）。‎ t的取值范围为：0＜t＜4。‎ ‎（2）结论：△AEF的面积S不变化。‎ ‎∵AOCD是矩形，∴AD∥OE，∴△AQD∽△EQC。‎ ‎∴，即，解得CE=。‎ 由翻折变换的性质可知：DF=DQ=4－t，则CF=CD+DF=8－t。‎ S=S梯形AOCF＋S△FCE－S△AOE=（OA+CF）•OC+CF•CE－OA•OE ‎= [4＋（8－t）]×8+（8－t）•－×4×（8＋）。‎ 化简得：S=32为定值。‎ 所以△AEF的面积S不变化，S=32。‎ ‎（3）若四边形APQF是梯形，因为AP与CF不平行，所以只有PQ∥AF。‎ 由PQ∥AF可得：△CPQ∽△DAF。‎ ‎∴CP：AD=CQ：DF，即8－2t：8= t：4－t，化简得t2－12t＋16=0，‎ 解得：t1=6+2，t2=。‎ 由（1）可知，0＜t＜4，∴t1=6+2不符合题意，舍去。‎ ‎∴当t=秒时，四边形APQF是梯形。‎ ‎2、如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC．CD上滑动，且E、F不与B．C．D重合．‎ ‎（1）证明不论E、F在BC．CD上如何滑动，总有BE=CF；‎ ‎（2）当点E、F在BC．CD上滑动时，分别探讨四边形AECF和△CEF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．‎ ‎【答案】解：（1）证明：如图，连接AC ‎∵四边形ABCD为菱形，∠BAD=120°，‎ ‎∠BAE+∠EAC=60°，∠FAC+∠EAC=60°，‎ ‎∴∠BAE=∠FAC。‎ ‎∵∠BAD=120°，∴∠ABF=60°。‎ ‎∴△ABC和△ACD为等边三角形。‎ ‎∴∠ACF=60°，AC=AB。∴∠ABE=∠AFC。‎ ‎∴在△ABE和△ACF中，∵∠BAE=∠FAC，AB=AC，∠ABE=∠AFC，‎ ‎∴△ABE≌△ACF（ASA）。∴BE=CF。‎ ‎（2）四边形AECF的面积不变，△CEF的面积发生变化。理由如下：‎ 由（1）得△ABE≌△ACF，则S△ABE=S△ACF。‎ ‎∴S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC，是定值。‎ 作AH⊥BC于H点，则BH=2，‎ ‎。‎ 由“垂线段最短”可知：当正三角形AEF的边AE与BC垂直时，边AE最短．‎ 故△AEF的面积会随着AE的变化而变化，且当AE最短时，正三角形AEF的面积会最小，‎ 又S△CEF=S四边形AECF﹣S△AEF，则此时△CEF的面积就会最大．‎ ‎∴S△CEF=S四边形AECF﹣S△AEF。‎ ‎∴△CEF的面积的最大值是。‎ （二） 由运动产生的线段和差问题（最值问题）‎ ‎1、如图所示，已知A，B为反比例函数图像上的两点，动 点P在x正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是【 】‎ A. B. C. D. ‎ ‎【答案】D。‎ ‎【考点】反比例函数综合题，待定系数法，曲线上点的坐标与方程的关系，三角形三边关系。‎ ‎【分析】∵把A，B分别代入反比例函数 得：y1=2，y2= ，‎ ‎∴A（ ，2），B（2， ）。‎ ‎∵在△ABP中，由三角形的三边关系定理得：|AP－BP|＜AB，‎ ‎∴延长AB交x轴于P′，当P在P′点时，PA－PB=AB，‎ 即此时线段AP与线段BP之差达到最大。‎ 设直线AB的解析式是y=kx+b，把A、B的坐标代入得：‎ ‎ ，解得：。∴直线AB的解析式是。‎ 当y=0时，x= ，即P（ ，0）。故选D。‎ ‎2、如图，抛物线l交x轴于点A（﹣3，0）、B（1，0），交y轴于点C（0，﹣3）．将抛物线l沿y轴翻折得抛物线l1．‎ ‎（1）求l1的解析式；‎ ‎（2）在l1的对称轴上找出点P，使点P到点A的对称点A1及C两点的距离差最大，并说出理由；‎ ‎【答案】解：（1）如图1，设经翻折后，点A．B的对应点分别为A1、B1，‎ 依题意，由翻折变换的性质可知A1（3，0），B1（﹣1，0），C点坐标不变，‎ ‎∴抛物线l1经过A1（3，0），B1（﹣1，0），C（0，﹣3）三点，‎ 设抛物线l1的解析式为y=ax2+bx+c，则 ‎，解得。‎ ‎∴抛物线l1的解析式为：y=x2﹣2x﹣3。‎ ‎（2）抛物线l1的对称轴为：x=，‎ 如图2，连接B1C并延长，与对称轴x=1交于点P，则点P即为所求。‎ 此时，|PA1﹣PC|=|PB1﹣PC|=B1C。‎ 设P′为对称轴x=1上不同于点P的任意一点，‎ 则有：|P′A﹣P′C|=|P′B1﹣P′C|＜B1C（三角形两边之差小于第三边），‎ ‎∴|P′A﹣P′C|＜|PA1﹣PC|，即|PA1﹣PC|最大。‎ 设直线B1C的解析式为y=kx+b，则 ‎，解得k=b=﹣3。∴直线B1C的解析式为：y=﹣3x﹣3。‎ 令x=1，得y=﹣6。∴P（1，﹣6）。‎ ‎3、如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．‎ ‎（1）抛物线及直线AC的函数关系式；‎ ‎（2）设点M（3，m），求使MN+MD的值最小时m的值；‎ ‎（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；‎ ‎（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．‎ ‎【答案】解：（1）由抛物线y=﹣x2+bx+c过点A（﹣1，0）及C（2，3）得，‎ ‎，解得。∴抛物线的函数关系式为。‎ 设直线AC的函数关系式为y=kx+n，由直线AC过点A（﹣1，0）及C（2，3）得 ‎，解得。‎ ‎∴直线AC的函数关系式为y=x+1。‎ ‎（2）作N点关于直线x=3的对称点N′，‎ ‎ 令x=0，得y=3，即N（0，3）。‎ ‎∴N′（6，3）‎ 由得 D（1，4）。‎ 设直线DN′的函数关系式为y=sx+t，则 ‎，解得。‎ ‎∴故直线DN′的函数关系式为。‎ 根据轴对称的性质和三角形三边关系，知当M（3，m）在直线DN′上时，MN+MD的值最小，‎ ‎∴。‎ ‎∴使MN+MD的值最小时m的值为。‎ ‎（3）由（1）、（2）得D（1，4），B（1，2），‎ ‎ ①当BD为平行四边形对角线时，由B、C、D、N的坐标知，四边形BCDN是平行四边形，此时，点E与点C重合，即E（2，3）。‎ ‎ ②当BD为平行四边形边时，‎ ‎∵点E在直线AC上，∴设E（x，x+1），则F（x，）。‎ 又∵BD=2‎ ‎∴若四边形BDEF或BDFE是平行四边形时，BD=EF。‎ ‎∴，即。‎ 若，解得，x=0或x=1（舍去），∴E（0，1）。‎ 若，解得，，∴E或E。‎ 综上，满足条件的点E为（2，3）、（0，1）、、。‎ ‎（4）如图，过点P作PQ⊥x轴交AC于点Q；过点C作CG⊥x轴于点G， ‎ 设Q（x，x+1），则P（x，﹣x2+2x+3）。‎ ‎∴。‎ ‎∴ ‎ ‎。‎ ‎ ∵，‎ ‎∴当时，△APC的面积取得最大值，最大值为。‎ ‎4、如图，已知抛物线经过A（4，0），B（2，3），C（0，3）三点．‎ ‎（1）求抛物线的解析式及对称轴．‎ ‎（2）在抛物线的对称轴上找一点M，使得MA+MB的值最小，并求出点M的坐标．‎ ‎（3）在抛物线上是否存在一点P，使得以点A、B、C、P四点为顶点所构成的四边形为梯形？若存在，请求出点P的坐标；若不存在，请说明理由．‎ ‎【答案】解：（1）∵抛物线经过A（4，0），B（2，3），C（0，3）三点，‎ ‎∴ ，解得。‎ ‎∴抛物线的解析式为：，其对称轴为：。‎ ‎（2）由B（2，3），C（0，3），且对称轴为x=1，可知点B、C是关于对称轴x=1的对称点。‎ 如图1所示，连接AC，交对称轴x=1于点M，连接MB，则MA＋MB=MA＋MC=AC，根据两点之间线段最短可知此时MA＋MB的值最小。‎ 设直线AC的解析式为y=kx＋b，‎ ‎∵A（4，0），C（0，3），∴ ，解得。‎ ‎∴直线AC的解析式为：y=x＋3。‎ 令x=1，得y= 。∴M点坐标为（1，）。‎ ‎（3）结论：存在。‎ 如图2所示，在抛物线上有两个点P满足题意：‎ ‎①若BC∥AP1，此时梯形为ABCP1。‎ 由B（2，3），C（0，3），可知BC∥x轴，则x轴与抛物线的另一个交点P1即为所求。‎ 在中令y=0，解得x1=-2，x2=4。‎ ‎∴P1（－2，0）。‎ ‎∵P1A=6，BC=2，∴P1A≠BC。‎ ‎∴四边形ABCP1为梯形。‎ ‎②若AB∥CP2，此时梯形为ABCP2。‎ 设CP2与x轴交于点N，‎ ‎∵BC∥x轴，AB∥CP2，∴四边形ABCN为平行四边形。∴AN=BC=2。∴N（2，0）。‎ 设直线CN的解析式为y=k1x+b1，则有： ，解得。‎ ‎∴直线CN的解析式为：y=x+3。‎ ‎∵点P2既在直线CN：y=x+3上，又在抛物线：上，‎ ‎∴x+3=，化简得：x2－6x=0，解得x1=0（舍去），x2=6。‎ ‎∴点P2横坐标为6，代入直线CN解析式求得纵坐标为－6。∴P2（6，－6）。‎ ‎∵ABCN，∴AB=CN，而CP2≠CN，∴CP2≠AB。∴四边形ABCP2为梯形。‎ 综上所述，在抛物线上存在点P，使得以点A、B、C、P四点为顶点所构成的四边形为梯形，点P的坐标为（－2，0）或（6，－6）。‎