- 2021-05-10 发布 |
- 37.5 KB |
- 11页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2015上海中考数学压轴专题之面积问题
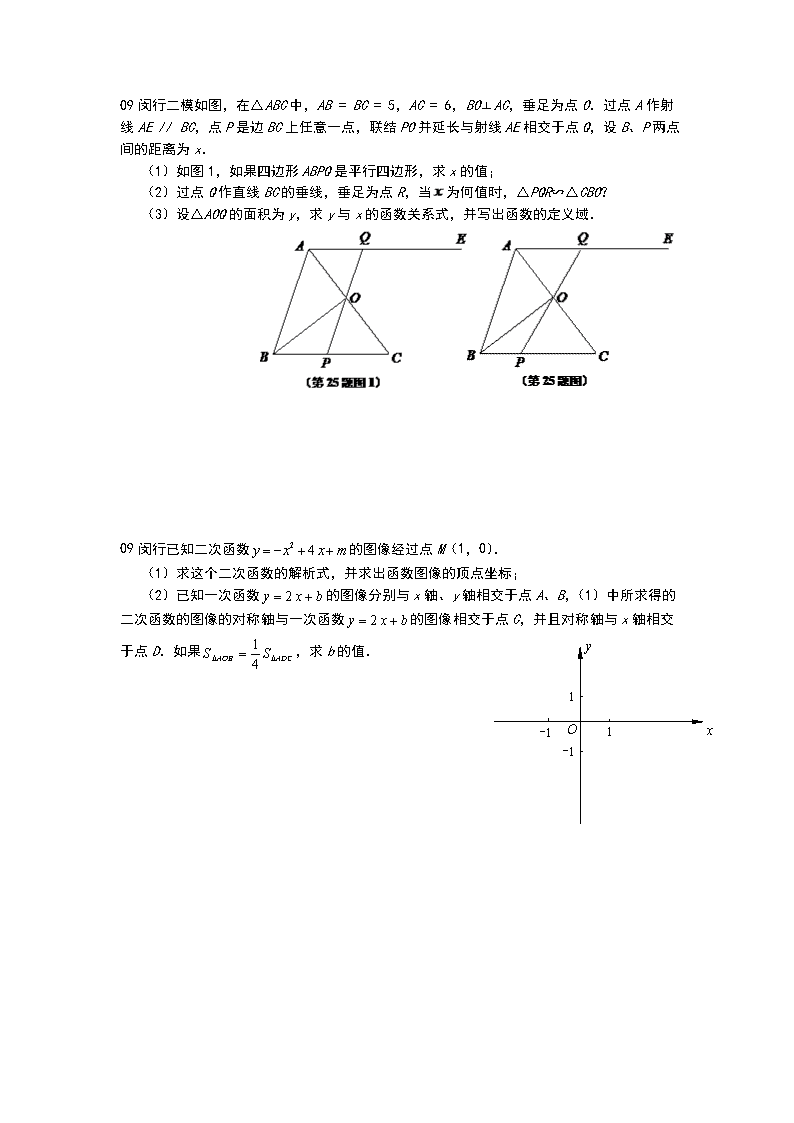
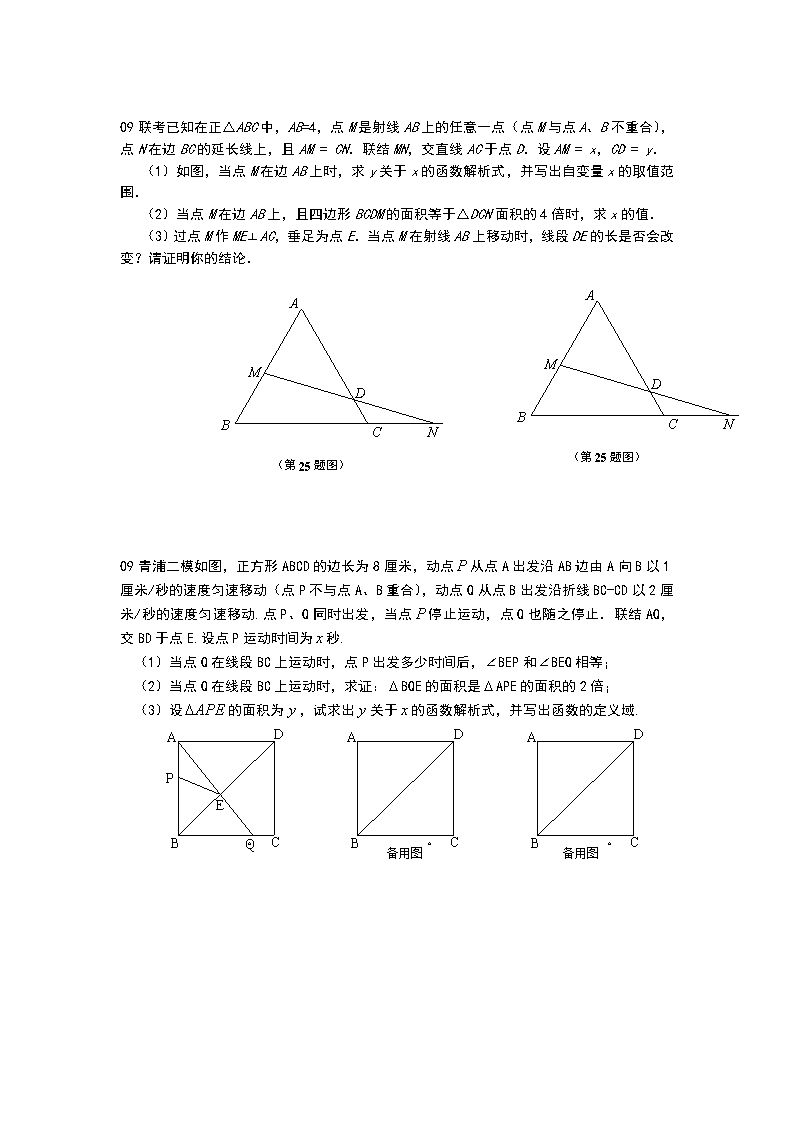
压轴之面积问题(09-12各区二模) 09奉贤二模.在平面直角坐标系中,矩形的边在轴正半轴上,边在轴的正半轴上,且,矩形绕点逆时针旋转后得到矩形,且点落在轴上的点,点的对应点为点A B C D E F x y O ,点的对应点为点. (1)求、、三点的坐标; (2)若抛物线经过点、、, 求此抛物线的解析式; (3)在轴上方的抛物线上求点Q的坐标,使得 三角形的面积等于矩形的面积? 09长宁二模.如图,一次函数图像交反比例函数图像于点M、N(N在M右侧),分别交x轴、y轴于点C、D。过点M、N作ME、NF分别垂直x轴,垂足为E、F。再过点E、F作EG、FH平行MN直线,分别交y轴于点G、H,ME交FH于点K。 (1)如果线段OE、OF的长是方程a2- 4a+3=0的两个根,求该一次函数的解析式; (2)设点M、N的横坐标分别为m、n,试探索四边形MNFK面积与四边形HKEG面积两者的数量关系; M N D C y O x E F H G K (3)求证:MD =CN。 09闵行二模如图,在△ABC中,AB = BC = 5,AC = 6,BO⊥AC,垂足为点O.过点A作射线AE // BC,点P是边BC上任意一点,联结PO并延长与射线AE相交于点Q,设B、P两点间的距离为x. (1)如图1,如果四边形ABPQ是平行四边形,求x的值; (2)过点Q作直线BC的垂线,垂足为点R,当为何值时,△PQR∽△CBO? (3)设△AOQ的面积为y,求y与x的函数关系式,并写出函数的定义域. 09闵行已知二次函数的图像经过点M(1,0). (1)求这个二次函数的解析式,并求出函数图像的顶点坐标; x y O -1 -1 1 1 (2)已知一次函数的图像分别与x轴、y轴相交于点A、B,(1)中所求得的二次函数的图像的对称轴与一次函数的图像相交于点C,并且对称轴与x轴相交于点D.如果,求b的值. 09联考已知在正△ABC中,AB=4,点M是射线AB上的任意一点(点M与点A、B不重合),点N在边BC的延长线上,且AM = CN.联结MN,交直线AC于点D.设AM = x,CD = y. (1)如图,当点M在边AB上时,求y关于x的函数解析式,并写出自变量x的取值范围. (2)当点M在边AB上,且四边形BCDM的面积等于△DCN面积的4倍时,求x的值. A B C M N D (第25题图) (3)过点M作ME⊥AC,垂足为点E.当点M在射线AB上移动时,线段DE的长是否会改变?请证明你的结论. A B C M N D (第25题图) 09青浦二模如图,正方形ABCD的边长为8厘米,动点从点A出发沿AB边由A向B以1厘米/秒的速度匀速移动(点P不与点A、B重合),动点Q从点B出发沿折线BC-CD以2厘米/秒的速度匀速移动.点P、Q同时出发,当点停止运动,点Q也随之停止.联结AQ,交BD于点E.设点P运动时间为秒. (1)当点Q在线段BC上运动时,点P出发多少时间后,∠BEP和∠BEQ相等; (2)当点Q在线段BC上运动时,求证:BQE的面积是APE的面积的2倍; · D C B A 备用图 · D C B A 备用图 · P D C B A E Q (3)设的面积为,试求出关于的函数解析式,并写出函数的定义域. 2010宝山二模如图9,矩形ABCD中,,点E是BC边上的一个动点,联结AE,过点D作,垂足为点F . (1)设,的余切值为y,求y关于x的函数解析式; (2)若存在点,使得ABE 、ADF与四边形CDFE的面积比是3:4:5, 试求矩形ABCD的面积;(备用图) · D C B A E F · D C B A E F (图9) 2010浦东二模如图,已知在矩形ABCD中,AB=3,BC=4,P是边BC延长线上的一点,联接AP交边CD于点E,把射线AP沿直线AD翻折,交射线CD于点Q,设CP=x,DQ=y. (1)求y关于x的函数解析式,并写出定义域. (2)当点P运动时,△APQ的面积是否会发生变化?如果发生变化,请求出△APQ的面积S关于x的函数解析式,并写出定义域;如果不发生变化,请说明理由. A B C Q D P E 2010松江二模如图,正方形ABCD中, AB=1,点P是射线DA上的一动点, DE⊥CP,垂足为E, EF⊥BE与射线DC交于点F. (1)若点P在边DA上(与点D、点A不重合). ①求证:△DEF∽△CEB; ②设AP=x,DF=y,求与的函数关系式,并写出函数定义域; A B C D A B C D E F P (2)当时,求AP的长. 2010闵行三模.如图,在直角坐标平面xOy内,点A在x轴的正半轴上,点B在第一象限内,且∠OAB = 90º,∠BOA = 30º,OB = 4.二次函数的图像经过点A,顶点为点C. (1)求这个二次函数的解析式,并写出顶点C的坐标; (2)设这个二次函数图像的对称轴l与OB相交于点D,与x轴相交于点E,求的值; y x C B A O l D E (第24题图) (3)设P是这个二次函数图像的对称轴l上一点,如果△POA的面积与△OCE的面积相等,求点P的坐标. 2011浦东二模如图,已知在直角坐标平面内,点A的坐标为(3,0),第一象限内的点P在直线y=2x上,∠PAO=45度. (1)求点P的坐标; (2)如果二次函数的图像经过P、O、A三点,求这个二次函数的解析式,并写出它的图像的顶点坐标M; (3)如果将第(2)小题中的二次函数的图像向上或向下平移,使它的顶点落在直线y=2x上的点Q处,求△APM与△APQ的面积之比. x y O 1 2 3 1 2 3 (第24题图) 2011闵行二模如图,已知:抛物线与x轴相交于A、B两点,与y轴相交于点C,并且OA = OC. (1)求这条抛物线的解析式; (2)过点C作CE // x轴,交抛物线于点E,设抛物线的顶点为点D,试判断△CDE的形状,并说明理由; x y O B A C D E l (3)设点M在抛物线的对称轴l上,且△MCD的面积等于△CDE的面积,请写出点M的坐标(无需写出解题步骤). 2011普陀二模直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角(且≠ 90°),得到Rt△, (1)如图9,当边经过点B时,求旋转角的度数; (2)在三角板旋转的过程中,边与AB所在直线交于点D,过点 D作DE∥交边于点E,联结BE. ①当时,设,,求与之间的函数解析式及定义域; ②当时,求的长. 图9 备用图 备用图 2011卢湾二模已知:抛物线经过点,,且对称轴与轴交于点. (1)求抛物线的表达式; (2)如图,点、分别是轴、对称轴上的点,且四边形是矩形,点是上一点,将沿着直线翻折,点与线段上的点重合,求点的坐标; (第24题图) (3)在(2)的条件下,点是对称轴上的点,直线交于点,,求点坐标. 2011杨浦二模已知△ABC中,AB=4,BC=6,AC>AB,点D为AC边上一点,且DC=AB,E为BC边的中点,联结DE,设AD=x。 (1) 当DE⊥BC时(如图1),求x的值; (2) 设,求y关于x的函数关系式,并写出定义域; A B C D E (备用图) D C E B A (图1) A y C B D O x E 2011松江二模如图,在平面直角坐标系xoy中,直角梯形OABC的顶点O为坐标原点,顶点A、C分别在x轴、y轴的正半轴上,CB∥OA, OC=4, BC=3,OA=5,点D在边OC上,CD=3,过点D作DB的垂线DE,交x轴于点E. (1)求点E的坐标; (2)二次函数的图象经过点B和点E. ①求二次函数的解析式和它的对称轴; ②如果点M在它的对称轴上且位于x轴上方, 满足,求点M的坐标. 2012松江二模已知直线分别与轴、轴交于点,B,抛物线经过点,B. (1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标; (2)记该抛物线的对称轴为直线l,点B关于直线l的对称点为C,若点D在轴的正半轴上,且四边形ABCD为梯形. ①求点D的坐标; O 1 1 x y ②将此抛物线向右平移,平移后抛物线的顶点为P,其对称轴与直线交于点E,若,求四边形BDEP的面积. x y O A B 12闵行二模已知:如图,抛物线与x轴的负半轴相交于点A,与y轴相交于点B(0,3),且∠OAB的余切值为. (1)求该抛物线的表达式,并写出顶点D的坐标; (2)设该抛物线的对称轴为直线l,点B关于直线l的对称点为C,BC与直线l相交于点E.点P在直线l上,如果点D是△PBC的重心,求点P的坐标; (3)在(2)的条件下,将(1)所求得的抛物线沿y轴向上或向下平移后顶点为点P,写出平移后抛物线的表达式.点M在平移后的抛物线上,且△MPD的面积等于△BPD的面积的2倍,求点M的坐标. 2012宝山二模已知△ABC中,(如图8),点到两边的距离相等,且PA=PB. (1)先用尺规作出符合要求的点P(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由; (2)设,,试用、的代数式表示的周长和面积; (3)设CP与AB交于点D,试探索当边AC、BC的长度变化时,的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由. A B C (备用图) A B C (图 ) 8 2012市调研已知:在Rt△ABC中,∠C=90°,AC=4,∠A=60°,CD是边AB上的中线,直线BM∥AC,E是边CA延长线上一点,ED交直线BM于点F,将△EDC沿CD翻折得△,射线交直线BM于点G. (1)如图1,当CD⊥EF时,求BF的值; (2)如图2,当点G在点F的右侧时; ①求证:△BDF∽△BGD; ②设AE=x,△DFG的面积为y,求y关于x的函数解析式,并写出x的取值范围; (第25题图1) B A C E D F M (第25题图2) B A C E D F M G (第25题备用图) B A C D M (3)如果△DFG的面积为,求AE的长.查看更多