中考数学模拟试题及答案8

中考数学模拟试题及答案8

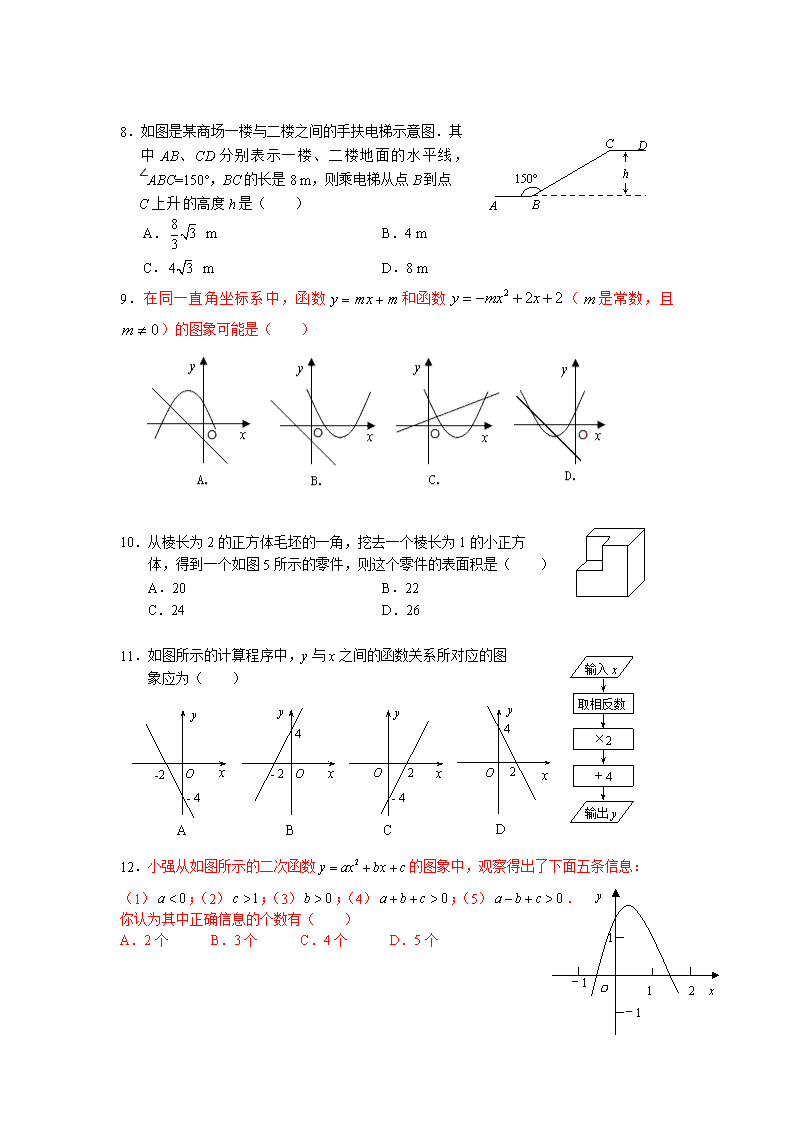
‎2011年中考模拟题 数　学　试　卷（八）‎ ‎*考试时间120分钟　试卷满分120分 一、选择题（本大题共12个小题，每小题2分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．若，则下列各式中一定成立的是（ ）‎ A． 　　　B．　　 C． 　　　 D． ‎ ‎2．一根笔直的小木棒（记为线段AB），它的正投影为线段CD，则下列各式中一定成立的是（ ）‎ A B O ‎·‎ C A．AB=CD B．≤ C． D．≥ ‎ ‎3．如图，两个同心圆的半径分别为‎3cm和‎5cm，弦AB与小圆相切于点 C，则AB的长为（　　）‎ ‎ A．‎4cm B．‎‎5cm ‎ C．‎6cm D．‎‎8cm ‎4．下列运算中，正确的是（ ）‎ P O B A A． B．‎ ‎ C． D．‎ ‎5．如图，四个边长为1的小正方形拼成一个大正方形，A、‎ B、O是小正方形顶点，⊙O的半径为1，P是⊙O上的点，‎ 且位于右上方的小正方形内，则∠APB等于（ ）‎ A．30° B．45° C．60° D．90° ‎ x y O A B ‎6．如图，在直角坐标系中，点是轴正半轴上的一个定点，点是 双曲线（）上的一个动点，当点的横坐标逐渐增大时，‎ 的面积将会 ‎ A．逐渐增大 B．不变 C．逐渐减小 D．先增大后减小 ‎7．甲、乙、丙三人进行乒乓球比赛，规则是：两人比赛，另一人当裁判，输者将在下一局中担任裁判，每一局比赛没有平局．已知甲、乙各比赛了4局，丙当了3次裁判．问第2局的输者是（　　）‎ A． 甲 B． 乙 C． 丙 D．不能确定 A B C D ‎150°‎ h ‎8．如图是某商场一楼与二楼之间的手扶电梯示意图．其 中AB、CD分别表示一楼、二楼地面的水平线，‎ ‎∠ABC=150°，BC的长是‎8 m，则乘电梯从点B到点 C上升的高度h是（ ）‎ A． m B．‎‎4 m C． m D．‎‎8 m ‎9．在同一直角坐标系中，函数和函数（是常数，且）的图象可能是（　　）‎ ‎10．从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方 体，得到一个如图5所示的零件，则这个零件的表面积是（ ）‎ A．20 B．22 ‎ C．24 D．26 ‎ 取相反数 ‎×2‎ ‎＋4‎ 输入x 输出y ‎11．如图所示的计算程序中，y与x之间的函数关系所对应的图 象应为（ ）‎ O y x ‎-2‎ ‎- 4‎ A D C B O ‎4‎ ‎2‎ y O ‎2‎ ‎- 4‎ y x O ‎4‎ ‎- 2‎ y x x x ‎1‎ y ‎2‎ ‎－1‎ ‎1‎ Ｏ ‎－1‎ ‎12．小强从如图所示的二次函数的图象中，观察得出了下面五条信息：‎ ‎（1）；（2）；（3）；（4）；（5）．‎ 你认为其中正确信息的个数有（ ）‎ A．2个 B．3个　　　C．4个　　　D．5个 二、填空题（本大题共6个小题，每小题3分，共18分．把答案写在题中横线上）‎ ‎13．比较大小：－6 －8．（填“＜”、“=”或“＞”）‎ ‎14．矩形内有一点P到各边的距离分别为1、3、5、7，则该矩形的最大面积为 平方单位．‎ ‎15．在一周内，小明坚持自测体温，每天3次．测量结果统计如下表： ‎ 体温（℃）‎ ‎36.1‎ ‎36.2‎ ‎36.3‎ ‎36.4‎ ‎36.5‎ ‎36.6‎ ‎36.7‎ 次 数 ‎2‎ ‎3‎ ‎4‎ ‎6‎ ‎3‎ ‎1‎ ‎2‎ 则这些体温的中位数是 ℃．‎ ‎16．观察下列等式：‎ ‎；‎ ‎；‎ ‎；‎ ‎…………‎ 则第（是正整数）个等式为________.‎ A B C D E A′‎ ‎17．如图，等边△ABC的边长为‎1 cm，D、E分别是AB、‎ AC上的点，将△ADE沿直线DE折叠，点A落在点 ‎ 处，且点在△ABC外部，则阴影部分图形的周长 为 cm．‎ ‎18．如图，矩形ABCD中，由8个面积均为1的小正方形组成 的L型模板如图放置，则矩形ABCD的周长为 _．‎ 三、解答题（本大题共8个小题，共78分．解答应写出文字说明、证明过程或演算步骤）‎ ‎19．（本小题满分8分）‎ 先化简，再求值：‎ 其中 ‎20．（本小题满分8分）‎ 某商场开展购物抽奖活动，抽奖箱中有4个标号分别为1、2、3、4的质地、大小相同的小球，顾客任意摸取一个小球，然后放回，再摸取一个小球，若两次摸出的数字之和为“‎8”‎是一等奖，数字之和为“‎6”‎是二等奖，数字之和为其它数字则是三等奖，请分别求出顾客抽中一、二、三等奖的概率.‎ 电视机月销量扇形统计图 第一个月 ‎15%‎ 第二个月 ‎30%‎ 第三个月 ‎25%‎ 第四个月 图11-1‎ ‎21．（本小题满分9分）‎ 某商店在四个月的试销期内，只销售A、B两个品牌的电视机，共售出400台．试销结束后，只能经销其中的一个品牌，为作出决定，经销人员正在绘制两幅统计图，如图11-1和图11-2．‎ 时间/月 ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎50‎ ‎40‎ ‎60‎ 图11-2‎ 销量/台 第一 第二 第三 第四 电视机月销量折线统计图 A品牌 B品牌 ‎80‎ ‎70‎ ‎（1）第四个月销量占总销量的百分比是 ；‎ ‎（2）在图11-2中补全表示B品牌电视机月销量的 折线；‎ ‎（3）为跟踪调查电视机的使用情况，从该商店第 四个月售出的电视机中，随机抽取一台，求 抽到B品牌电视机的概率；‎ ‎（4）经计算，两个品牌电视机月销量的平均水平相 同，请你结合折线的走势进行简要分析，判断 该商店应经销哪个品牌的电视机．‎ ‎22．（本小题满分9分）‎ 某天，小明来到体育馆看球赛，进场时，发现门票还在家里，此时离比赛开始还有25分钟，于是立即步行回家取票.同时，他父亲从家里出发骑自行车以他3倍的速度给他送票，两人在途中相遇，相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段、分别表示父、子俩送票、取票过程中，离体育馆的路程（米）与所用时间（分钟）之间的函数关系，结合图象解答下列问题（假设骑自行车和步行的速度始终保持不变）：‎ S（米）‎ t（分）‎ B O O ‎3 600‎ ‎15‎ A ‎（1）求点的坐标和所在直线的函数关系式；‎ ‎（2）小明能否在比赛开始前到达体育馆？‎ ‎23．（本小题满分10分）‎ 已知：如图，在△ABC中，∠ABC＝90°，以AB上的点O为圆心，OB的长为半径的圆与AB交于点E，与AC切于点D．‎ ‎（1）求证：BC＝CD；‎ ‎（2）求证：∠ADE＝∠ABD；‎ ‎（3）设AD＝2，AE＝1，求⊙O直径的长．‎ ‎24．（本小题满分10分）‎ 图1‎ A H C(M)‎ D E B F G(N)‎ G 图2‎ A H C D E B F N M A H C D E 图3‎ B F G M N 在图1至图3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．‎ ‎（1）如图1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，‎ 求证：FM = MH，FM⊥MH；‎ ‎（2）将图-1中的CE绕点C顺时针旋转一个锐角，得到图2，‎ 求证：△FMH是等腰直角三角形；‎ ‎（3）将图2中的CE缩短到图3的情况，‎ ‎△FMH还是等腰直角三角形吗？（不必 说明理由）‎ ‎25．（本小题满分12分）‎ 如图，某公路隧道横截面为抛物线，其最大高度为‎6米，底部宽度OM为‎12米. 现以O点为原点，OM所在直线为x轴建立 直角坐标系.‎ ‎(1)直接写出点M及抛物线顶点P的坐标；‎ ‎(2)求这条抛物线的解析式；‎ ‎(3)若要搭建一个矩形“支撑架”AD- DC- CB，‎ 使C、D点在抛物线上，A、B点在地面OM上，‎ ‎26．（本小题满分12分）‎ 如图，平行四边形ABCD中，AB＝5，BC＝10，BC边上的高AM=4，E为 BC边上的一个动点（不与B、C重合）．过E作直线AB的垂线，垂足为F． FE与DC的延长线相交于点G，连结DE，DF．‎ ‎（1） 求证：ΔBEF ∽ΔCEG．‎ ‎（2） 当点E在线段BC上运动时，△BEF和△CEG的周长之间有什么关系？并说明你的理由．‎ ‎（3）设BE＝x，△DEF的面积为 y，请你求出y和x之间的函数关系式，并求出当x为何值时,y有最大值，最大值是多少？ ‎ ‎2011年中考模拟题（八）‎ 数学试题参考答案及评分标准 一、选择题 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 A D D C B C C B D C D C 二、填空题 ‎13．＞； 14．64； 15．36.4； 16．； 17．3； 18．．‎ 三、解答题 ‎19．解：÷= 3分 ‎ =x+4 5分 当x =3时，原式=3+4‎ ‎ =7 8分 ‎20．解：抽中一等奖的概率为， 3分 抽中二等奖的概率为， 5分 抽中三等奖的概率为． 8分 ‎ ‎ 时间/月 ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎50‎ ‎40‎ ‎60‎ 图1‎ 销量/台 第一 第二 第三 第四 电视机月销量折线统计图 A品牌 B品牌 ‎80‎ ‎70‎ ‎ ‎ ‎21．解：（1）30%； ‎ ‎（2）如图1；‎ ‎（3）；‎ ‎（4）由于月销量的平均水平相同，从折线的走势看，‎ A品牌的月销量呈下降趋势，而B品牌的月销量呈上升趋势． ‎ 所以该商店应经销B品牌电视机．‎ S（米）‎ t（分）‎ B O O ‎3 600‎ ‎15‎ ‎22．解：（1）解法一：‎ 从图象可以看出：父子俩从出发到相遇时花费了15分钟 1分 设小明步行的速度为x米/分，则小明父亲骑车的速度为3x米/分 依题意得：15x+45x=3600． 2分 解得：x=60．‎ 所以两人相遇处离体育馆的距离为 ‎60×15=‎900米．‎ 所以点B的坐标为（15，900）． 3分 设直线AB的函数关系式为s=kt+b（k≠0）． 4分 由题意，直线AB经过点A（0，3600）、B（15，900）得：‎ 解之，得 ‎∴直线AB的函数关系式为：． 6分 解法二：‎ 从图象可以看出：父子俩从出发到相遇花费了15分钟． 1分 设父子俩相遇时，小明走过的路程为x米．‎ 依题意得： 2分 解得x=900，所以点B的坐标为（15，900） 3分 以下同解法一．‎ ‎（2）解法一：小明取票后，赶往体育馆的时间为： 7分 小明取票花费的时间为：15+5=20分钟．‎ ‎∵20<25‎ ‎∴小明能在比赛开始前到达体育馆． 9分 解法二：在中，令S=0，得．‎ ‎ 解得：t=20．‎ 即小明的父亲从出发到体育馆花费的时间为20分钟，因而小明取票的时间也为20分钟． ∵20<25，∴小明能在比赛开始前到达体育馆． 9分 ‎23．解：（1）∵∠ABC＝90°，‎ ‎∴OB⊥BC． 1分 ‎∵OB是⊙O的半径，‎ ‎∴CB为⊙O的切线． 2分 又∵CD切⊙O于点D，‎ ‎∴BC＝CD； 3分 ‎（2）∵BE是⊙O的直径，‎ ‎∴∠BDE＝90°．‎ ‎∴∠ADE＋∠CDB ＝90°． 4分 又∵∠ABC＝90°，‎ ‎∴∠ABD＋∠CBD＝90°． 5分 由（1）得BC＝CD，∴∠CDB ＝∠CBD．‎ ‎∴∠ADE＝∠ABD； 6分 ‎（3）由（2）得，∠ADE＝∠ABD，∠A＝∠A．‎ ‎∴△ADE∽△ABD． 7分 ‎∴＝． 8分 ‎∴＝，∴BE＝3， 9分 ‎∴所求⊙O的直径长为3． 10分 ‎24．（1）证明：∵四边形BCGF和CDHN都是正方形，‎ 又∵点N与点G重合，点M与点C重合，‎ ‎∴FB = BM = MG = MD = DH，∠FBM =∠MDH = 90°．‎ ‎∴△FBM ≌ △MDH．‎ ‎∴FM = MH． ‎ ‎∵∠FMB =∠DMH = 45°，∴∠FMH = 90°．∴FM⊥HM．‎ 图2‎ A H C D E B F G N M P ‎（2）证明：连接MB、MD，如图2，设FM与AC交于点P．‎ ‎∵B、D、M分别是AC、CE、AE的中点，‎ ‎∴MD∥BC，且MD = BC = BF；MB∥CD，‎ 且MB=CD=DH．‎ ‎∴四边形BCDM是平行四边形．‎ ‎∴ ∠CBM =∠CDM．‎ 又∵∠FBP =∠HDC，∴∠FBM =∠MDH．‎ ‎∴△FBM ≌ △MDH．‎ ‎∴FM = MH， ‎ 且∠MFB =∠HMD．‎ ‎∴∠FMH =∠FMD－∠HMD =∠APM－∠MFB =∠FBP = 90°．‎ ‎∴△FMH是等腰直角三角形． ‎ ‎（3）是．‎ ‎25．解：(1) M(12，0)，P(6，6). 2分 ‎(2) 设抛物线解析式为：. 3分 ‎∵抛物线经过点(0，0)，‎ ‎∴，即 4分 ‎∴抛物线解析式为：‎ ‎ . 5分(3) 设A(m，0)，则 B(12-m，0)，，. 7分 ‎∴“支撑架”总长AD+DC+CB = ‎ ‎=. 10分 ‎ ∵ 此二次函数的图象开口向下.‎ ‎∴ 当m = ‎3米时，AD+DC+CB有最大值为‎15米. 12分 ‎ ‎ ‎26． （1） 因为四边形ABCD是平行四边形， 所以 1分 ‎ 所以 所以 3分 ‎（2）的周长之和为定值． 4分 理由一：‎ 过点C作FG的平行线交直线AB于H ，‎ 因为GF⊥AB，所以四边形FHCG为矩形．所以 FH＝CG，FG＝CH 因此，的周长之和等于BC＋CH＋BH ‎ 由 BC＝10，AB＝5，AM＝4，可得CH＝8，BH＝6，‎ 所以BC＋CH＋BH＝24 6分 理由二：‎ 由AB＝5，AM＝4，可知 ‎ 在Rt△BEF与Rt△GCE中，有：‎ ‎，‎ 所以，△BEF的周长是， △ECG的周长是 又BE＋CE＝10，因此的周长之和是24． 6分 ‎（3）设BE＝x，则 所以 8分 配方得：． ‎ 所以，当时，y有最大值． 10分 最大值为． 12分 ‎ ‎